Ch ng 3 Ph ng pháp ươ ươ
th ng kê xác su t trong ố ấ
thu vănỷ

I. M t s ki n th c c b n v lý ộ ố ế ứ ơ ả ề
thuy t xác su tế ấ
Phép th :ử
Đ c hi u là các th nghi m ho c các quan ượ ể ử ệ ặ
sát đ c th c hi n đ i v i m t hi n t ng ượ ự ệ ố ớ ộ ệ ượ
ng u nhiên nào đó. Các th nghi m và các ẫ ử ệ
quan sát đó ph i đ c th c hi n trong cùng ả ượ ự ệ
m t đi u ki n nh t đ nh.ộ ề ệ ấ ị
K t qu c a phép th ng u nhiên g i là bi n ế ả ủ ử ẫ ọ ế
c ng u nhiên, ho c nói ng n g n là bi n c .ố ẫ ặ ắ ọ ế ố

Phân lo i bi n cạ ế ố
Bi n c ch c ch n: là bi n c nh t đ nh ph i xu t hi n trong ế ố ắ ắ ế ố ấ ị ả ấ ệ
m t phép th .ộ ử
Bi n c không th có: là bi n c không th xu t hi n trong m t ế ố ể ế ố ể ấ ệ ộ
phép th .ử
Bi n c đ c l p: là bi n c mà s xu t hi n c a nó không ph ế ố ộ ậ ế ố ự ấ ệ ủ ụ
thu c vào s xu t hi n c a các bi n c khácộ ự ấ ệ ủ ế ố
Bi n c ph thu c: là bi n c mà s xu t hi n c a nó ph ế ố ụ ộ ế ố ự ấ ệ ủ ụ
thu c vào s xu t hi n c a bi n c khácộ ự ấ ệ ủ ế ố
Bi n c xung kh c: Hai bi n c A và B đ c g i là hai bi n c ế ố ắ ế ố ượ ọ ế ố
xung kh c n u chúng không cùng xu t hi n trong m t phép ắ ế ấ ệ ộ
th .ử
Bi n c đ i l p: ế ố ố ậ A đ c g i là đ i l p v i bi n c A n u bi n ượ ọ ố ậ ớ ế ố ế ế
c ốA và bi n c A không x y ra trong phép th nh ng m t ế ố ả ử ư ộ
trong hai bi n c ch c ch n ph i xu t hi n.ế ố ắ ắ ả ấ ệ
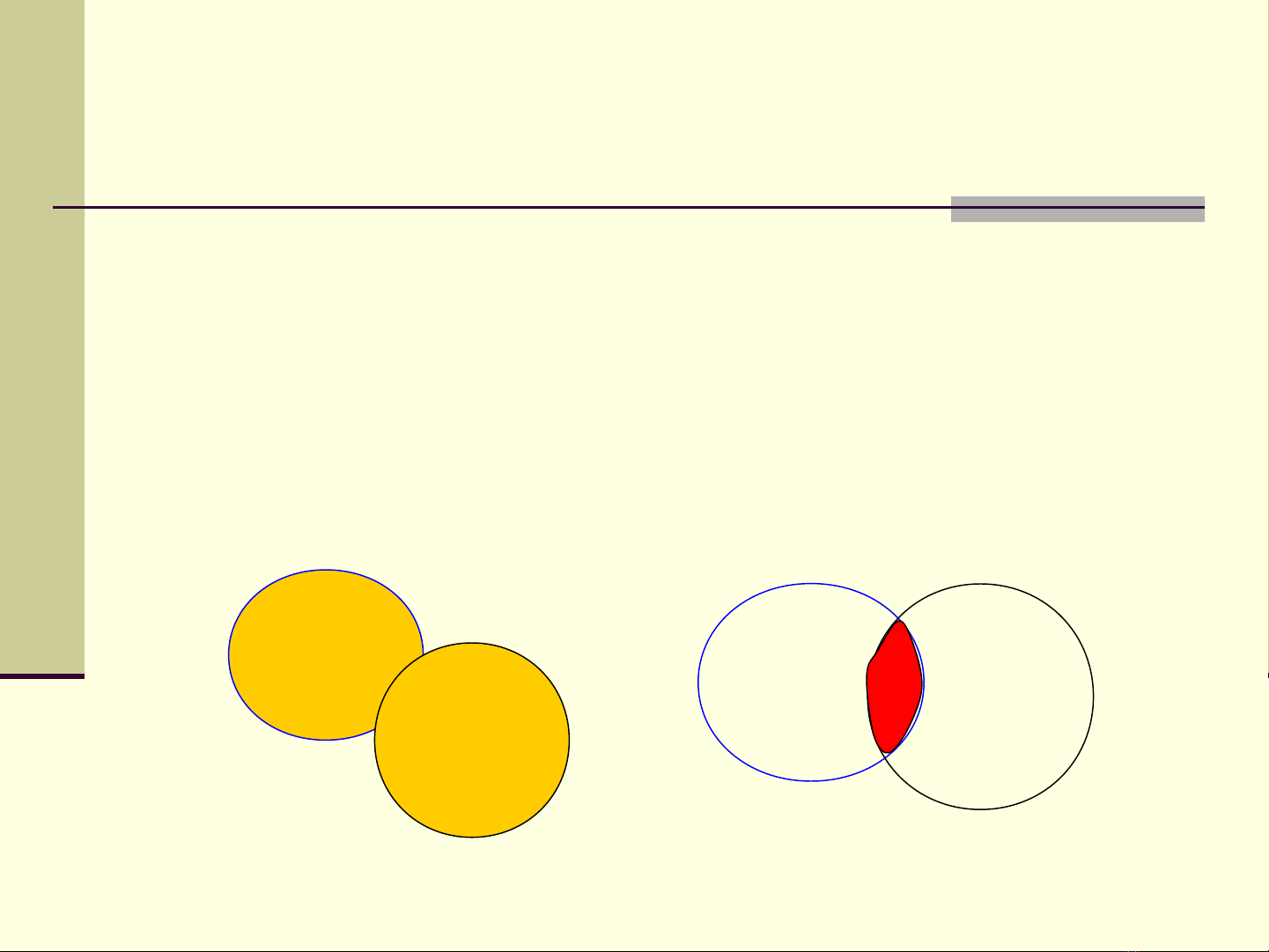
Bi n c t ng: bi n c C đ c g i là bi n c t ng ế ố ổ ế ố ượ ọ ế ố ổ
c a hai bi n c A và B n u ho c A xu t hi n, ho c ủ ế ố ế ặ ấ ệ ặ
B xu t hi n, ho c c A và B cùng xu t hi n.ấ ệ ặ ả ấ ệ
Bi n c tích: Bi n c C đ c g i là bi n c tích c a ế ố ế ố ượ ọ ế ố ủ
hai bi n c A và B n u bi n c C xu t hi n là do ế ố ế ế ố ấ ệ
bi n c A và B cùng xu t hi n t o nên.ế ố ấ ệ ạ
A
B
C=A+B
A
B
C=A.B
Phân lo i bi n c (ti p)ạ ế ố ế

Đ nh nghĩa xác su tị ấ
Đ nh nghĩa c đi n:ị ổ ể
Xác su t xu t hi n c a m t bi n c A nào đó ấ ấ ệ ủ ộ ế ố
b ng t s gi a s bi n c c b n thu n l i ằ ỷ ố ữ ố ế ố ơ ả ậ ợ
cho A xu t hi n trên t ng các bi n c c b n ấ ệ ổ ế ố ơ ả
c a không gian bi n c .ủ ế ố
Công th c tính xác su t c a bi n c A là:ứ ấ ủ ế ố
Trong đó: n là t ng s các bi n c c b n c a ổ ố ế ố ơ ả ủ
không gian bi n c đang xét; m là s bi n c c ế ố ố ế ố ơ
b n thu n l i cho bi n c A xu t hi n.ả ậ ợ ế ố ấ ệ
n
m
AP
=
)(


























