Bài Giảng Toán 12 - Chân Trời Sáng Tạo - Chương 1 - Bài 3: Đường Tiệm Cận Của Đồ Thị Hàm Số

Việc nghiên cứu hành vi của các hàm số và biểu diễn đồ thị của chúng đóng vai trò nền tảng trong chương trình Toán học phổ thông. Đặc biệt, việc thấu hiểu các đặc điểm của đồ thị hàm số tại các điểm giới hạn hoặc khi biến số tiến tới vô cùng là cực kỳ quan trọng. Khái niệm đường tiệm cận cung cấp cái nhìn sâu sắc về xu hướng tiệm cận của đồ thị, giúp phân tích toàn diện hơn về tính chất của hàm số. Bài giảng này, thuộc chương trình "Chân trời sáng tạo" Toán 12, tập trung giới thiệu và làm rõ các loại tiệm cận chính, bao gồm tiệm cận đứng và tiệm cận ngang, trang bị kiến thức cơ bản nhưng vững chắc cho học sinh.

Học sinh lớp 12 đang học chương trình Toán học phổ thông, giáo viên Toán THPT, và những cá nhân quan tâm tìm hiểu kiến thức cơ bản về giới hạn và các loại đường tiệm cận của hàm số.

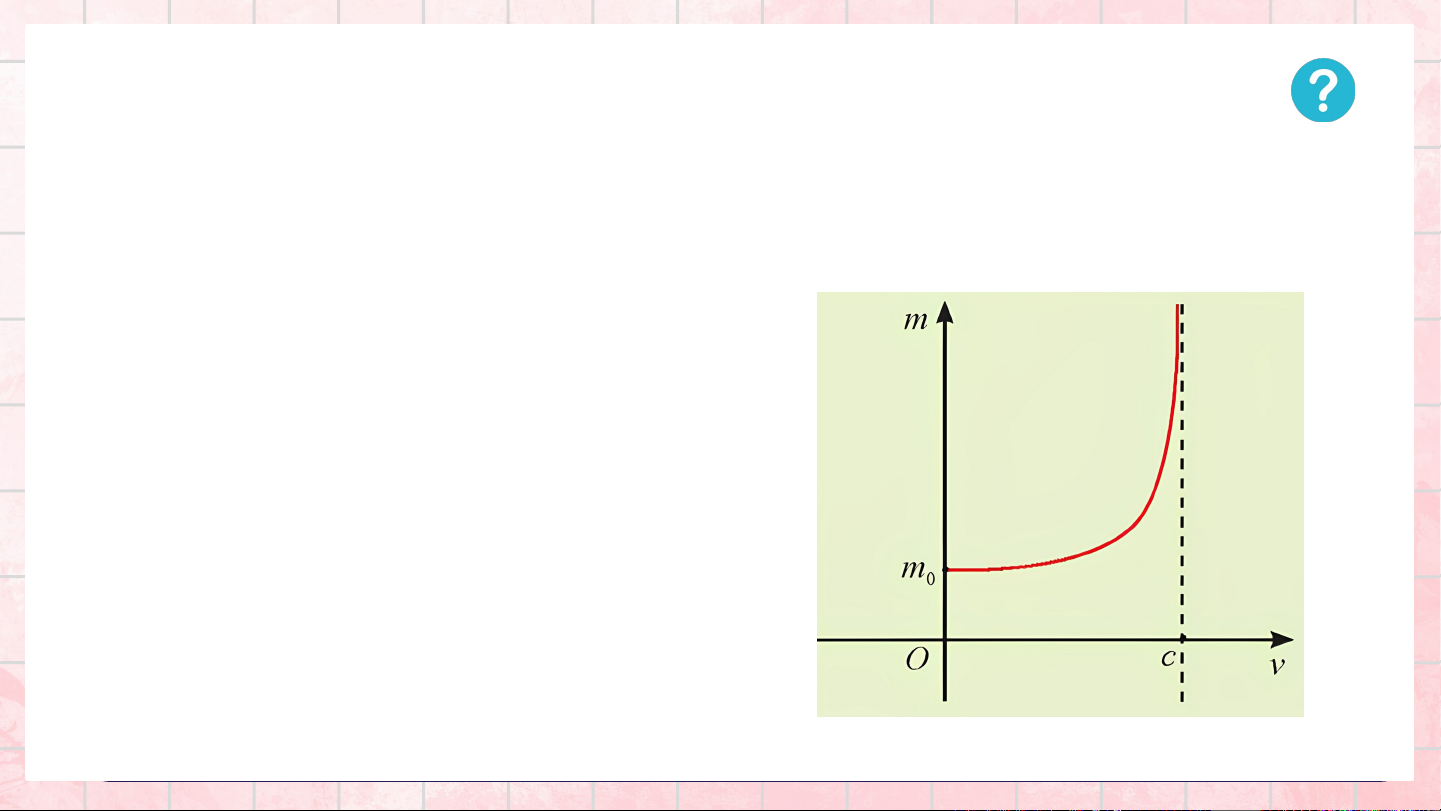
Bài giảng điện tử này được thiết kế cho học sinh Toán 12 theo chương trình "Chân trời sáng tạo", cung cấp một cái nhìn tổng quan và chi tiết về đường tiệm cận của đồ thị hàm số. Mở đầu với phần "Khởi động" đầy thú vị, bài giảng sử dụng ví dụ thực tế từ thuyết tương đối hẹp để minh họa ý tưởng về giới hạn và sự tiệm cận, khơi gợi hứng thú và liên hệ kiến thức toán học với các hiện tượng vật lý. Nội dung chính tập trung vào việc định nghĩa và phân tích hai loại tiệm cận quan trọng: tiệm cận đứng và tiệm cận ngang. Mỗi loại được giải thích cặn kẽ thông qua định nghĩa toán học dựa trên khái niệm giới hạn, các ví dụ minh họa cụ thể về cách tìm đường tiệm cận cho các hàm số khác nhau, và đặc biệt là các hình ảnh đồ thị rõ ràng để trực quan hóa cách đồ thị hàm số tiến gần đến các đường tiệm cận. Phương pháp giảng dạy kết hợp lý thuyết và thực hành, với các "Hoạt động khám phá" và "Thực hành" nhằm củng cố sự hiểu biết và kỹ năng ứng dụng của học sinh. Mặc dù mục lục đề cập đến tiệm cận xiên, phần nội dung trình bày chủ yếu xoay quanh hai loại tiệm cận đầu tiên. Nắm vững kiến thức về đường tiệm cận là nền tảng thiết yếu giúp học sinh vẽ đồ thị chính xác, phân tích hành vi của hàm số và giải quyết các bài toán liên quan đến giới hạn, có ứng dụng rộng rãi không chỉ trong toán học mà còn trong các lĩnh vực khoa học khác.