
V T LÝ CH T R N ĐI C NGẬ Ấ Ắ Ạ ƯƠ
TÀI LI U THAM KH O TRONG:Ệ Ả
Đ NG C U NỖ Ọ Ấ
GIÁO TRÌNH V T LÝ CH T R N ĐI C NGẬ Ấ Ắ Ạ ƯƠ
NXB KHOA H C &K THU TỌ Ỹ Ậ
HÀ N I 2003Ộ
L U Ý: ƯINTRODUCTION TO SOLID STATE
PHYSICS
C A C. KITTELỦ
Tu nầN i dungộ
1 Ch ng I: C u trúc tu n hoàn c a ươ ấ ầ ủ
tinh thể
2 Ti p Ch ng Iế ươ
3 Ch ng II: Tính ch t c h c c a ươ ấ ơ ọ ủ
v t r n tinh thậ ắ ể
4 Ti p Ch ng IIế ươ
5 Ch ng III: Phonon và dao đng ươ ộ
m ngạ
6 Ch ng IV: Tính ch t nhi t c a ươ ấ ệ ủ
các ch t đi n môiấ ệ

7 Ti p Ch ng IV, Bài t pế ươ ậ
8 Bài t p các ch ng 1, 2, 3, 4ậ ươ
9 Ki m tra gi a kì, Ch ng V: Khí đi n t t do Fermiể ữ ươ ệ ử ự
10 Ti p Ch ng V: Khí đi n t t do Fermiế ươ ệ ử ự
11 Ch ng VI: Lý thuy t vùng năng l ngươ ế ượ
12 Ti p ch ng VI: Lý thuy t vùng năng l ng, ế ươ ế ượ
ch ng VII: M t Fermi trong kim lo iươ ặ ạ
13 Ti p ch ng VII: M t Fermi trong kim lo i . Bài t p ế ươ ặ ạ ậ
ch ng: 5, 6ươ
14 Ch ng VIII: Các tinh th bán d n, ch ng IX: Tính ươ ể ẫ ươ
diêu d nẫ
15 Ch ng X:Các tính ch t c a đi n môi, ch ng XI: ươ ấ ủ ệ ươ
Tính ch t t c a ch t r n, ch ng XII: Ch t r n vô ấ ừ ủ ấ ắ ươ ấ ắ
đnh hìnhị

Tinh th và vô đnh hìnhể ị
•Môi tr ng liên t c: khi b c sóng kh o sát ườ ụ ướ ả
l n h n kho ng cách gi a các nguyên t (ớ ơ ả ữ ử >
a)
Tinh th : Có tr t t xa, tu n hoànể ậ ự ầ
Vô đnh hình: Tr t t g n, vô tr t tị ậ ự ầ ậ ự
• Môi tr ng không liên t c: Khi b c sóng ườ ụ ướ
kh o sát nh h n ho c b ng kho ng cách gi a ả ỏ ơ ặ ằ ả ữ
các nguyên t (ử <= a)
Ch ng Iươ
C U TRÚC TU N HOÀN C A TINH THẤ Ầ Ủ Ể
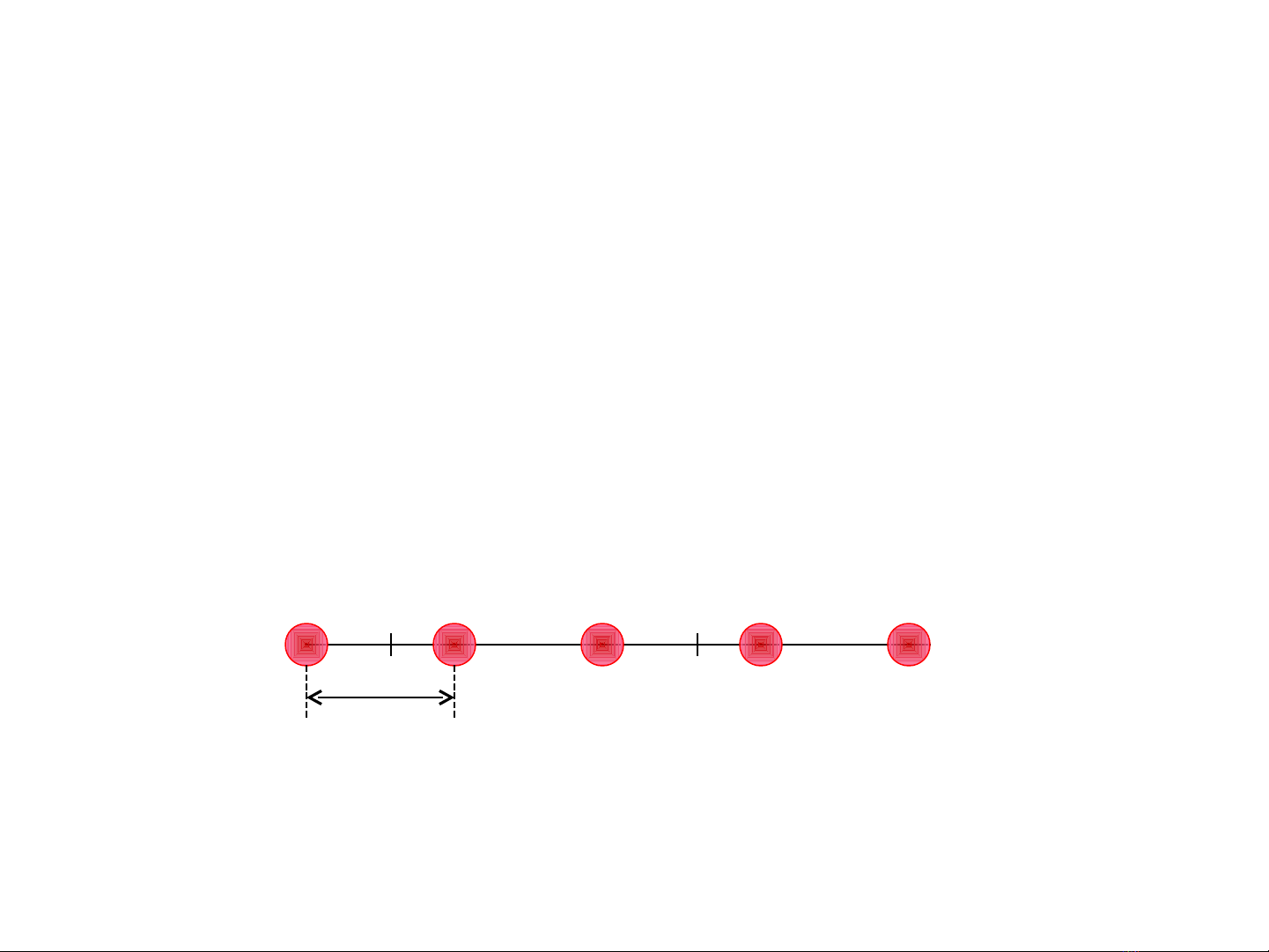
I. Mô hình c u trúc tu n hoànấ ầ c a v t ủ ậ
r n tinh th :ắ ể Phép t nh ti n...ị ế
•T nh ti n đi m t véc t t nh ti n-> l p l i ị ế ộ ơ ị ế ặ ạ
nh đi m xu t phát ư ể ấ
•T nh ti n ô c s l p đy không gianị ế ơ ở ấ ầ
a
T = na
B’B
anT
1




















![Bộ câu hỏi lý thuyết Vật lý đại cương 2 [chuẩn nhất/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251003/kimphuong1001/135x160/74511759476041.jpg)
![Bài giảng Vật lý đại cương Chương 4 Học viện Kỹ thuật mật mã [Chuẩn SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250925/kimphuong1001/135x160/46461758790667.jpg)




