zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Công Nghệ Thông Tin

» Đồ họa - Thiết kế - Flash

Bài giảng Xử lý ảnh số: Các phép biến đổi ảnh - Nguyễn Linh Giang (p2)

Chia sẻ: Minh Vũ | Ngày: | Loại File: PDF | Số trang:12

Báo xấu

198
lượt xem 23
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng "Xử lý ảnh số: Các phép biến đổi ảnh (p2)" cung cấp cho người học các kiến thức về các phép biến đôi ảnh bao gồm: Biến đổi sin, cosin, biến đổi Hadamar, biến đổi Haar, biến đổi K-L. Mời các bạn cùng tham khảo.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Xử lý ảnh số: Các phép biến đổi ảnh - Nguyễn Linh Giang (p2)

Xử lý ảnh số Các phép biến đổi ảnh Chương trình dành cho kỹ sư CNTT Nguyễn Linh Giang
Các phép biến đổi ảnh • Biến đổi đơn nguyên ( unitary ) • Biến đổi Fourier • Biến đổi sin, cosin • Biến đổi Hadamar • Biến đổi Haar • Biến đổi K-L
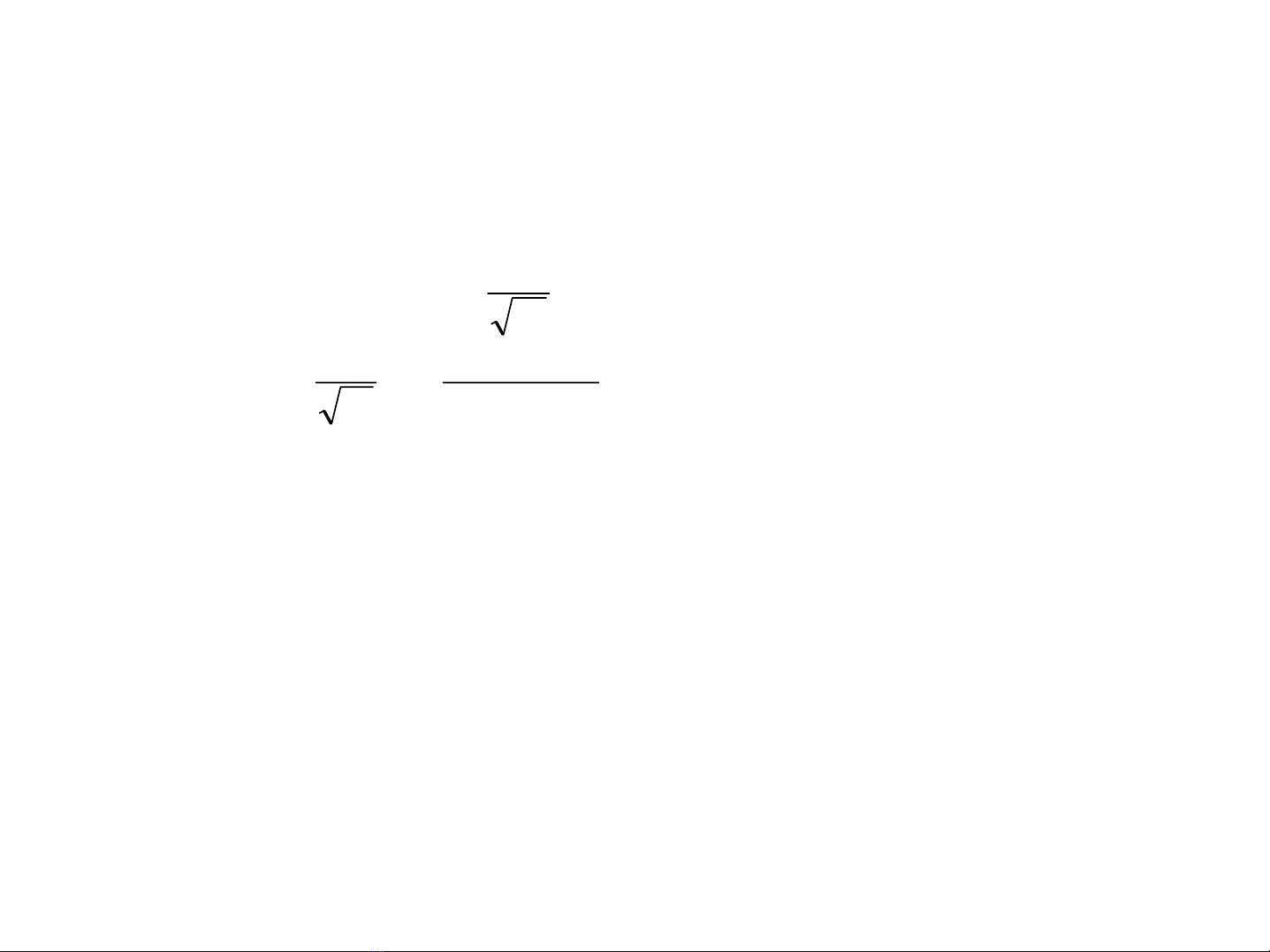
Phép biến đổi cosine DCT • Ma trận biến đổi DCT: ⎧ 1 ⎪⎪ k = 0, 0 ≤ n ≤ N - 1 c( k , l ) = ⎨ N 2 π (2n + 1)k ⎪ cos( ) 1 ≤ k ≤ N − 1;0 ≤ n ≤ N − 1 ⎪⎩ N 2N – C = ||c(k,l)||NxN – C = C*; C-1 = CT – Phép biến đổi: V=CSCT; S = CTVC
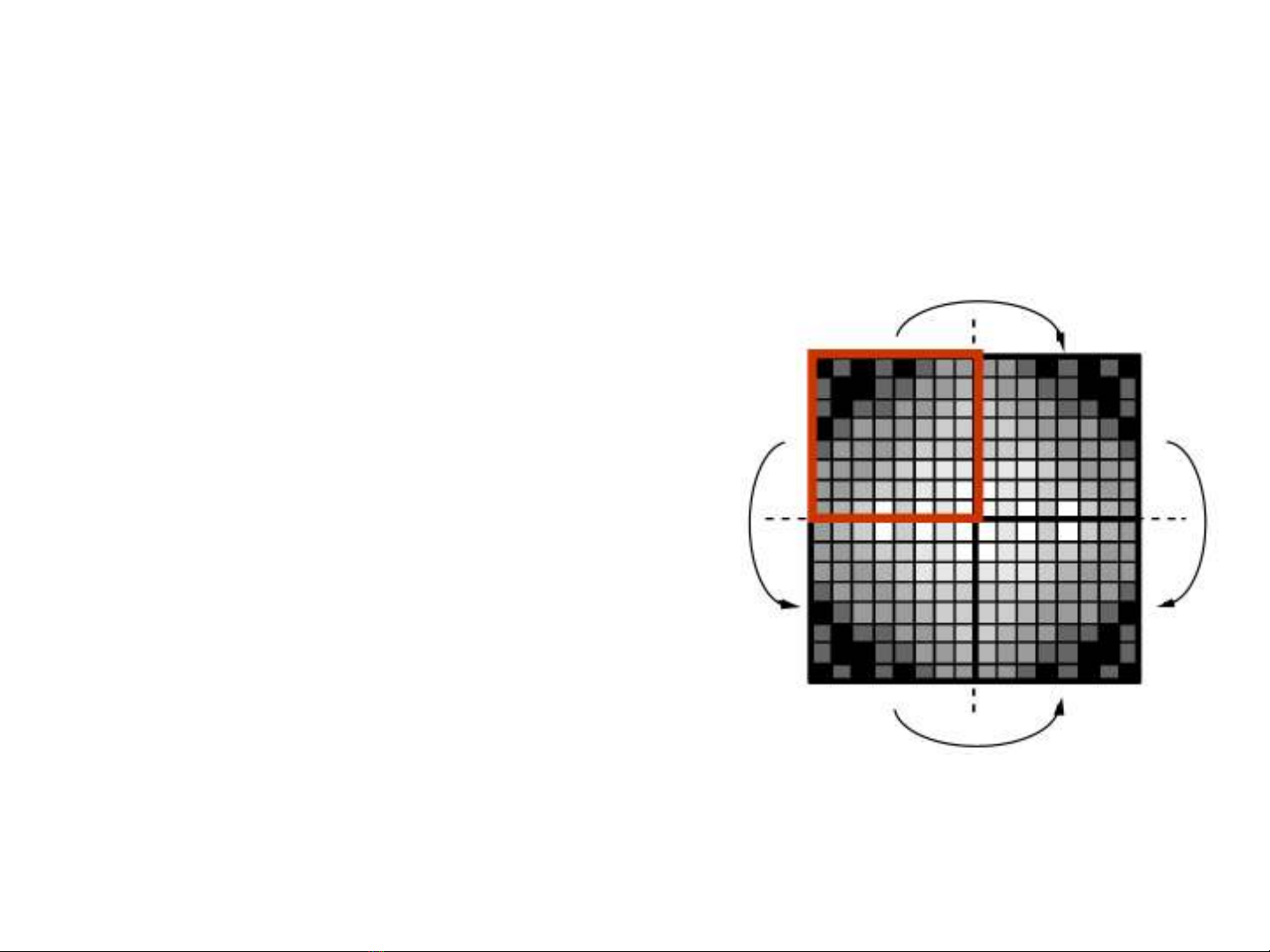
Phép biến đổi cosine DCT • Tính chất phép biến đổi DCT – Ma trận C là ma trận thực; – Ma trận C không đối xứng; – Là phép biến đổi đơn nguyên và trực giao; – DCT không phải là phần thực của UDFT • Liên hệ với DFT qua phép đối xứng tín hiệu: mở rộng tín hiệu bằng cách đối xứng qua gốc tọa độ. – Là phép biến đổi nhanh
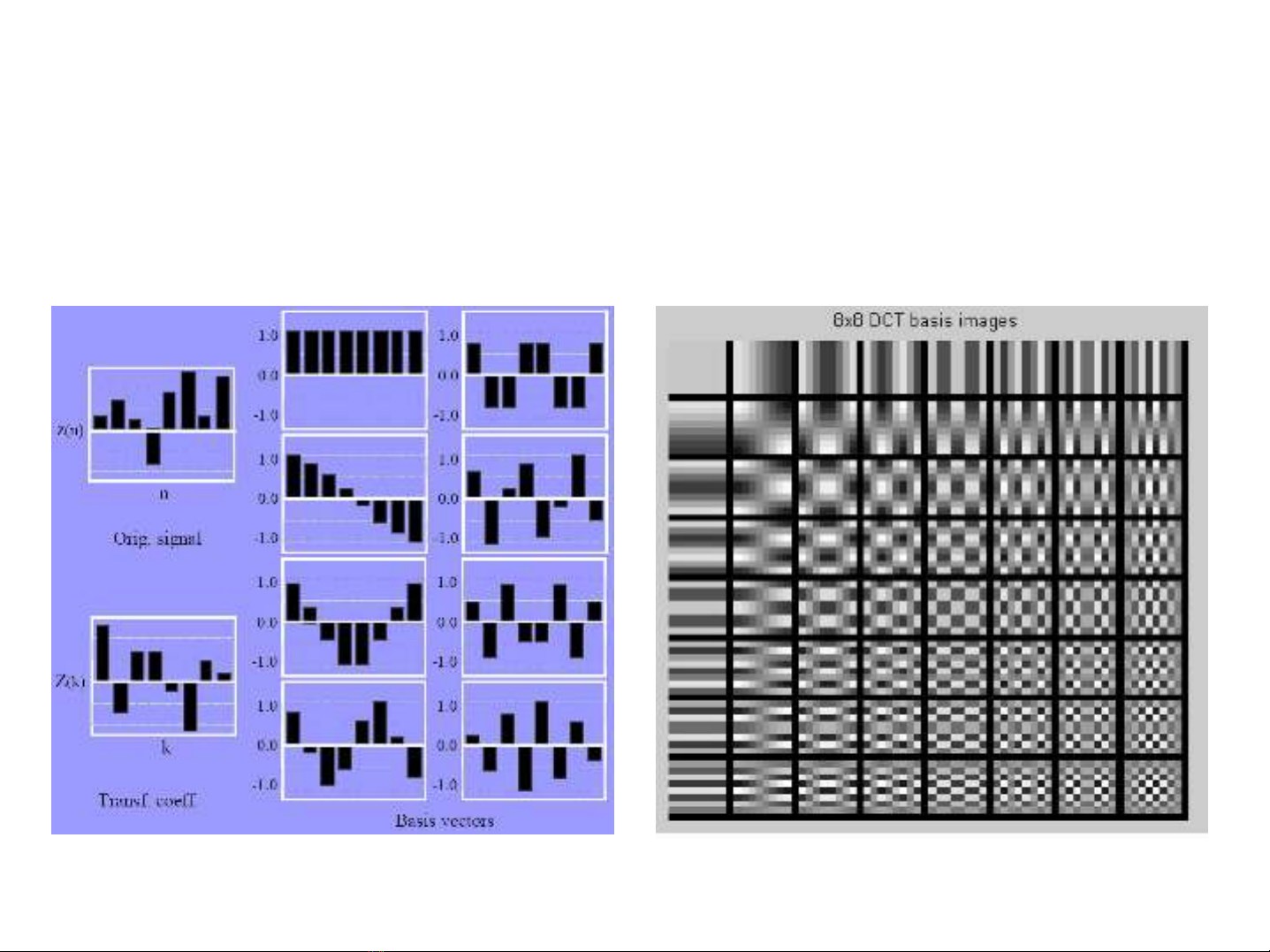
Phép biến đổi cosine DCT – Ảnh cơ sở của DCT:
Phép biến đổi sine • Ma trận biến đổi 2 π ( k + 1)( n + 1) ψ (k , n) = Sin , 0 ≤ k, n ≤ N - 1 N +1 N +1 • Ψ = ||ψ(k,n)||NxN • Ψ = Ψ* = ΨT = Ψ*T • Biến đổi sine: V = ΨS Ψ; S = ΨV Ψ
Biến đổi Hadamar • Các vector cơ sở có thành phần bằng 1 hoặc -1 • N = 2n • Hệ thức truy hồi xây dựng ma trận H: 1 1 1 H2 = 2 1 −1 1 HN HN H 2N = 2 HN H −N – Ví dụ 1 1 1 1 1 1 −1 1 −1 H4 = 2 1 1 −1 −1 1 −1 −1 1
Biến đổi Hadamar • Khai triển biến đổi Hadamar V = HS S = HV 1 N −1 v(k ) = ∑ N n =0 s ( n )( − 1) b ( k ,n ) – Khai triển: 1 N −1 s ( n) = ∑ N k =0 v ( k )( − 1) b ( k ,n ) n −1 b(k , n) = ∑ ki ni i =0 – Trong đó {ki}, {ni} là biểu diễn nhị phân của k và n k = k0 + 2k1 + ... + 2m-1km-1 n = n0 + 2n1 + ... + 2m-1nm-1
Biến đổi Hadamar • Tính chất: – Là phép biến đổi đối xứng; – Là phép biến đổi đơn nguyên; – Là phép phân tích ảnh thành tổ hợp tuyến tính các xung vuông – Là phép biến đổi nhanh; – Nén năng lượng đối với những tín hiệu ảnh có độ tương quan cao.
Phép biến đổi Haar • Ma trận biến đổi: ⎡ ⎢ 1 1 1 1 1 1 1 1⎤ ⎥ ⎢ 1 1 1 1 −1 −1 −1 − 1⎥ ⎢ 2 2 − 2 − 2 0 0 0 0⎥ ⎢ ⎥ 1 ⎢ 0 0 0 0 2 2 − 2 − 2⎥ Hr = 8⎢ 2 −2 0 0 0 0 0 0⎥ ⎢ ⎥ ⎢ 0 0 2 −2 0 0 0 0⎥ ⎢ ⎥ ⎢ 0 0 0 0 2 −2 0 0⎥ ⎢⎣ 0 0 0 0 0 0 2 − 2⎥⎦
Phép biến đổi Haar • Cơ sở phép biến đổi
Phép biến đổi Haar • Tính chất của phép biến đổi Haar • Phép biến đổi Haar là thực và trực giao: Hr = Hr* Hr-1 = HrT • Phép biến đổi Haar là phép biến đổi nhanh. Các véctơ cơ sở của ma trận Haar được sắp xếp liên tục • Phép biến đổi Haar có khả năng nén năng lượng kém nhất trong các phép biến đổi đơn nguyên.

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.