Đề 1.
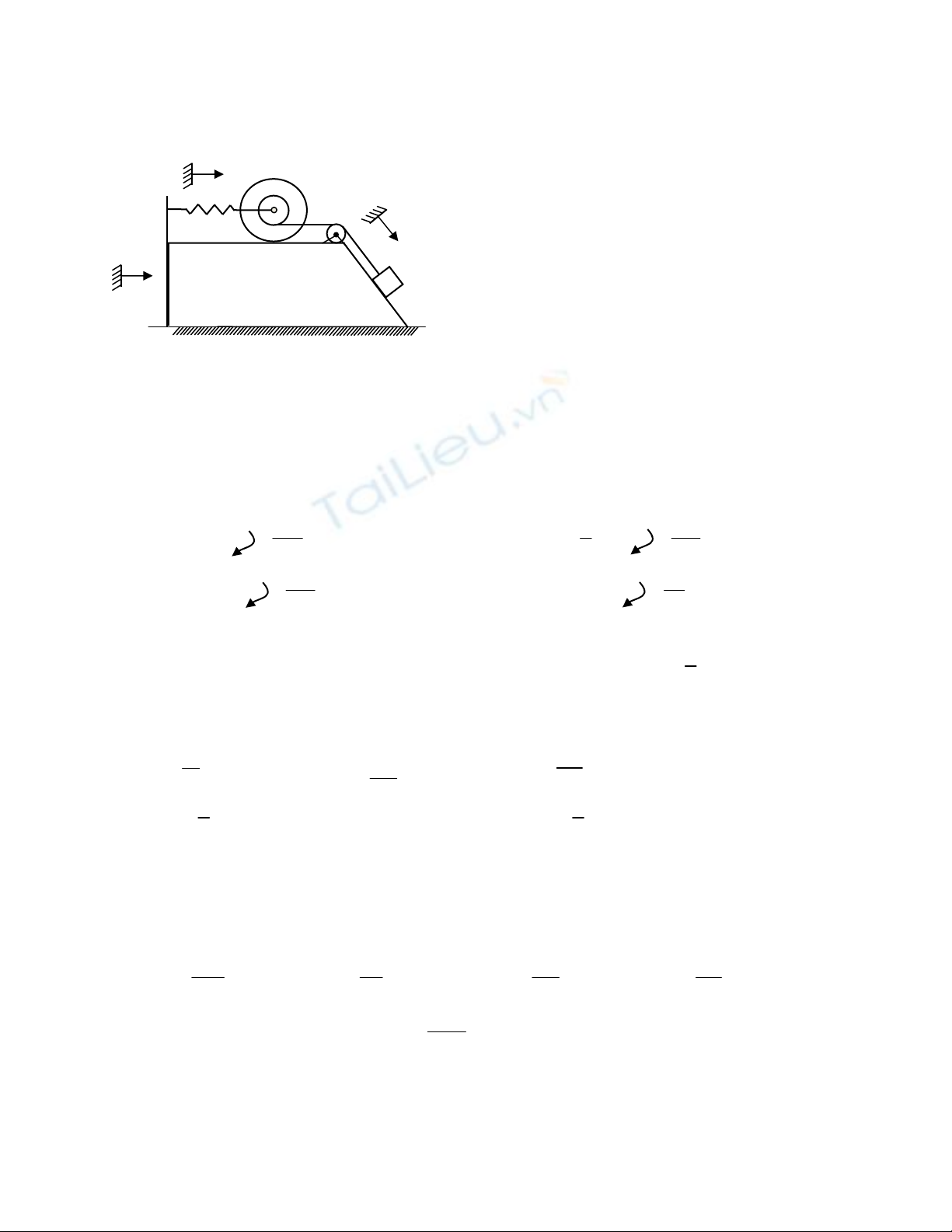
Cho cơ hệ như hình vẽ. Tải A, con lăn B và lăng trụ
C lần lượt có các khối lượng m1, m2, m3 = 3m2. Bán
kín trong của con lăn r, bán kính ngoài của con lăn
R, mô men quán tính của con lăn đối với trục đi qua
tâm B và vuông góc với mặt phẳng hình vẽ là JB =
m2.r2. Độ cứng của lò xo là K. Chỉ tồn tại ma sát
trượt tại tiếp điểm H có hệ số ma sát chung cho cả
tĩnh và động là f = 0,4. Giả sử con lăn lăn không
trượt. Các đại lượng được tính đều có thứ nguyên tương ứng với hệ đơn vị cơ bản.
I. Lăng trụ C được giữ cố định. Chọn độ dời s của A, x của tâm B có chiều như hình vẽ, gốc
tương ứng vị trí cân bằng tĩnh của cơ hệ. Các vectơ nằm bên phải của các đại lượng chỉ chiều
chuyển động.
Hãy chọn kết quả đúng ?
1/ Cho R =1,5r
a. 2
3,
A
BA
V
VV r
ω
→= ↓ = b. 3
2,
32
A
BA
V
VV r
ω
→= ↓ =
c. 3
1, 5 ,
A
BA
V
VV r
ω
→= ↓ = d. 2,
A
BA
V
VV r
ω
→= ↓ =
2/ Động năng T của cơ hệ khi cho R = 3r; m1 = 1,5m2
a. 2
2
5A
TmV= b. 2
2
2A
TmV= c. 2
2
7A
TmV= d. 2
2
4
3
A
TmV=
3/ Gọi x0 là độ giãn của lò xo, F là lực ma sát tác động lên con lăn tại H trong trạng thái cân bằng
tĩnh (chỉ chịu tác động của trọng lực). Cho R = 1,5r.
a.
01
1
2sin
1sin
2
xmg
K
Fmg
α
α
⎧=
⎪
⎪
⎨
⎪←=
⎪
⎩
b. 01
1
3sin
2
2sin
xmg
K
Fmg
α
⎧=
⎪
⎨
⎪←=
⎩
c.
01
1
1sin
3
2sin
3
xmg
K
Fmg
α
α
⎧=
⎪
⎪
⎨
⎪←=
⎪
⎩
d.
01
1
2sin
sin
xKmg
Fmg
α
α
=
⎧
⎨←=
⎩
4/ Tổng công ∑A của nội và ngoại lực tác động vào cơ hệ từ vị trí ban đầu (gốc tọa độ) đến vị trí
đang xét. Cho R = 1,5r.
a. 2
2,5
A
Ks=−
∑ b. 2
4
A
Ks=−
∑ c. 2
2,5
A
Ks=−
∑
d. 2
4,5
A
Ks=−
∑
5/ Cho R = 2r, m1 = 3m2, T = 4m2(VA)2, ∑A = -0,5Kx2. Tính gia tốc WA của tải A.
a.
2
2
A
K
Ws
m
=− b.
2
A
K
Ws
m
=− c.
2
2
A
K
Ws
m
=− d.
2
3
A
K
Ws
m
=−
6/ Cho R = 1,5r; m1 = m2; gia tốc
2
9
14
A
K
Ws
m
=− . Lập phương trình vi phân chuyển động của cơ
hệ theo độ dời x của tâm B.
A
s
x
s2
KB
I
C
H
a.
2
90
7
K
xx
m
+=
 b.
2
90
14
K
xx
m
+=
 c.
2
4,5 0
14
K
xx
m
+
=
 d.
2
90
7
K
xx
m
+
=

7/ Cho R = 3r; m1 = 1,5m2 ; 0
2
9
cos .
16
K
ss t
m
⎛⎞
=⎜⎟
⎜⎟
⎝⎠
. Tính sức căng dây τ.
a.
20
2
0
15 9
3sin cos .
32 16
sin
Diêu kiên 2
K
mg Ks t
m
g
sK
τα
α
⎧⎛⎞
=+
⎪⎜⎟
⎜⎟
⎪⎝⎠
⎨
⎪≤
⎪
⎩
b.
20
2
0
39
sin cos .
16 16
5sin
Diêu kiên 2
K
mg Ks t
m
g
sK
τα
α
⎧⎛⎞
=+
⎪⎜⎟
⎜⎟
⎪⎝⎠
⎨
⎪≤
⎪
⎩
c.
20
2
2
0
27 9
1, 5 sin cos .
32 16
16 sin
Diêu kiên 9
K
mg Ks t
m
mg
sK
τα
α
⎧⎛⎞
=+
⎪⎜⎟
⎜⎟
⎪⎝⎠
⎨
⎪≤
⎪
⎩
d.
20
2
2
0
17 9
2sin cos .
616
9sin
Diêu kiên 16
K
mg Ks t
m
mg
sK
τα
α
⎧⎛⎞
=+
⎪⎜⎟
⎜⎟
⎪⎝⎠
⎨
⎪≤
⎪
⎩
8/ Cho R = 3r; m1 = 1,5m2 ; 0
2
9
cos .
16
K
ss t
m
⎛⎞
=⎜⎟
⎜⎟
⎝⎠
. Tính lực ma sát F tác động vào con lăn tại
H.
a.
()
20
2
2
0
99
sin cos .
816
16
Không truot 0,4 0,5sin
3
K
Fmg Ks t
m
mg
sK
α
α
⎧⎛⎞
←= +
⎪⎜⎟
⎜⎟
⎪⎝⎠
⎨
⎪≤−
⎪
⎩
b.
()
20
2
2
0
299
sin cos .
31616
8
Không truot 0,4 0,75sin
9
K
Fmg Ks t
m
mg
s
α
α
⎧⎛⎞
←= +
⎪⎜⎟
⎜⎟
⎪⎝⎠
⎨
⎪≤−
⎪
⎩
c.
()
20
2
2
0
99
sin cos .
16 16
8
Phai có 0, 4 0,75sin
9
K
Fmg Ks t
m
mg
s
α
α
⎧⎛⎞
←= +
⎪⎜⎟
⎜⎟
⎪⎝⎠
⎨
⎪≤−
⎪
⎩
d.
()
20
2
2
0
39
0,5 sin cos .
16 16
8
Phai có 0, 4 0,75sin
K
Fmg Ks t
m
mg
sK
α
α
⎧⎛⎞
←= +
⎪⎜⎟
⎜⎟
⎪⎝⎠
⎨
⎪≤−
⎪
⎩

II Cho lăng trụ C có thể dịch chuyển trên nền ngang không ma sát. Chọn tọa độ suy rộng thứ
nhất q1 ≡ s1 là độ dời của tải A so với lăng trụ C, có gốc trùng vị trí cân bằng tĩnh (s1 ≡ s), chiều
đi xuống, q2 ≡ s2 (chiều từ trái sang phải) là độ dời của lăng trụ C.
9/ Cho R = 1,5r. Tính 22
,
A
B
VV
qua 12
,
s
s

.
a.
222
1212
222
12 12
cos
96
A
B
Vssss
Vssss
α
⎧=++
⎪
⎨=++
⎪
⎩

 b.
222
12 12
222
12 12
2cos
96
A
B
Vss ss
Vssss
α
⎧=++
⎪
⎨=++
⎪
⎩


c.
222
12 12
222
12 12
2
44
A
B
Vss ss
Vssss
⎧=++
⎪
⎨=++
⎪
⎩


d.
222
12 12
222
12 12
42cos
44
A
B
Vssss
Vssss
α
⎧=++
⎪
⎨=++
⎪
⎩


10/ Cho R = 3r; m1 = 1,5m2; 222
12 12
2
A
Vss ss=++

; 222
12 12
93
4
B
Vssss=++

. Tính động năng T
của cơ hệ ?
a. 22
21 2 2 212
326Tms ms mss=++

b. 22
21 2 2 212
223Tms ms mss=++


c. 22
21 22 212
1, 5 3 4Tmsmsmss=++

d. 22
21 22 212
221,5Tms ms mss=++

11/ Cho R =3r; m1 = 1,5m2. Tính các lực suy rộng của cơ hệ.
a. 11
22
9QKs
Qmg
=−
⎧
⎨=
⎩ b. 11
2
9
4
0
QKs
Q
⎧=−
⎪
⎨
⎪=
⎩
c. 11
2
3
2
0
QKs
Q
⎧=−
⎪
⎨
⎪=
⎩
d. 11
2
5
2
0
QKs
Q
⎧=−
⎪
⎨
⎪=
⎩
12/ Cho R = 2r; m1 = 3m2, 22
21 22 212
422Tmsmsmss=++

, Q1 = -4Ks1, Q2 = 0. Phương trình vi
phân chuyển động của cơ hệ:

a.
21 22 1
21 22
43
24 0
ms ms Ks
ms ms
+=−
⎧
⎨+=
⎩
 
  b.
21 22 1
21 2 2
26 4
24 0
ms ms Ks
ms ms
+=−
⎧
⎨+=
⎩
 
 
c. 21 2 2 1
21 22
42
24 0
ms ms Ks
ms ms
+=−
⎧
⎨+=
⎩
 
  d. 21 2 2 1
21 22
63 4
40
ms ms Ks
ms ms
+=−
⎧
⎨+=
⎩
 
 
13/ Cho 12
,
s
s
  , m1 = 1,5m2. Tính áp lực N của lăng trụ lên nền.
a. 221
5, 5 1, 5 sinNmgms
α
=−
 b. 221
4,5 1, 5 cosNmgms
α
=
−
c. 221 22
5, 5 3 sinNmgms ms
α
=− +
   d. 221 22
4, 5 3 sinNmgms ms
α
=
−+
 