Nguy n Văn Quy n – 0938.59.6698 – s u t m và biên so nễ ề ư ầ ạ
TU N 29ẦTOÁN 6
ÔN T P CH NG II – HÌNH H CẬ ƯƠ Ọ
PH N I. BÀI T PẦ Ậ
Câu h i 1:ỏ
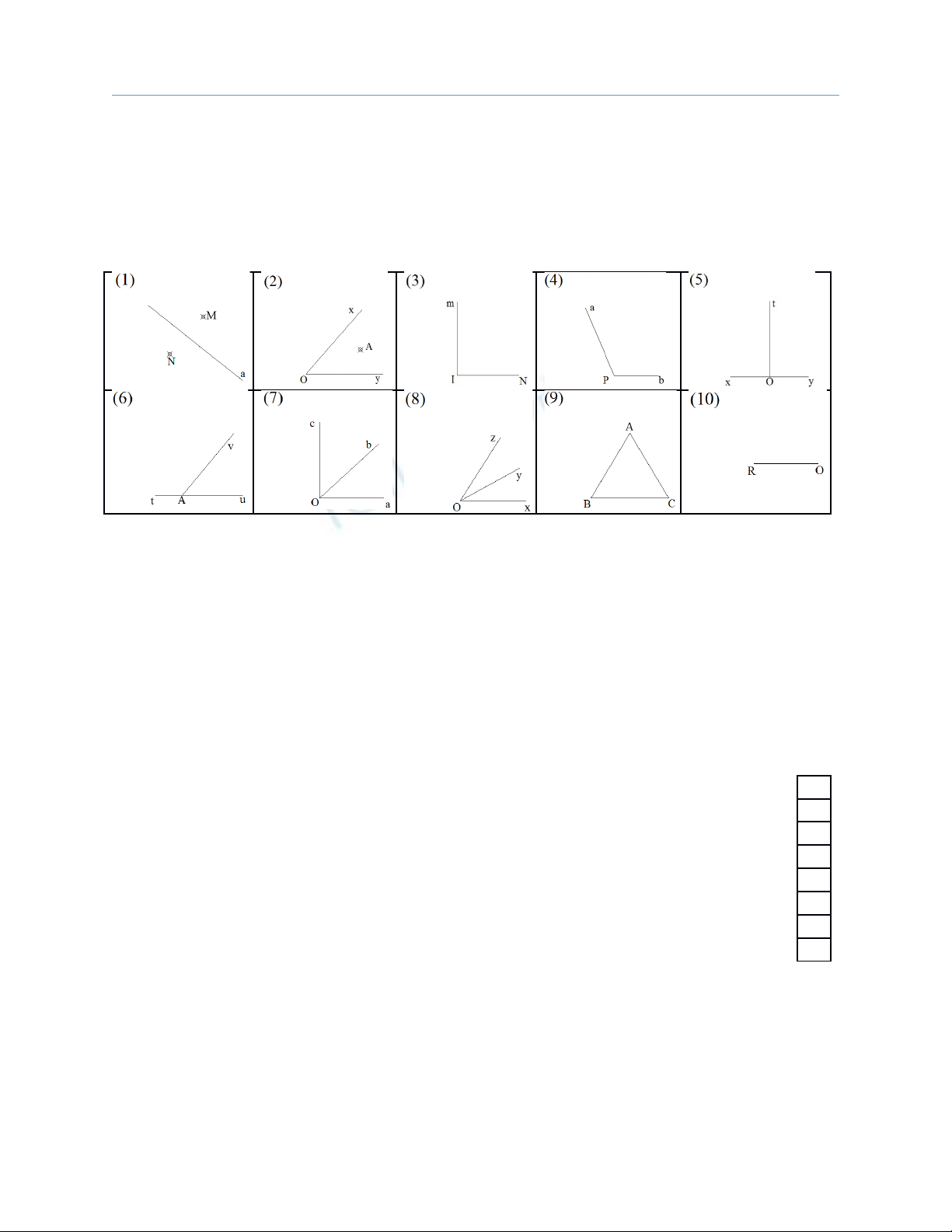
M i hình trong b ng trên cho ta bi t nh ng gì? ỗ ả ế ữ
Câu h i 2:ỏ Đi n vào ô tr ng các phát bi u sau đ đc m t câu đúng:ề ố ể ể ượ ộ
a) B t k đng th ng nào trên m t ph ng cũng là ………. c a ……………………….ấ ỳ ườ ẳ ặ ẳ ủ
b) M i góc có m t ………. s đo c a góc b t b ng …………………………………….ỗ ộ ố ủ ẹ ằ
c) N u tia Ob n m gi a hai tia Oa và Oc thì ……………………………………………ế ằ ữ
d) N u thì ……………………………………………………………ế
Câu h i 3:ỏ Đúng hay sai ?
a) Góc là m t hình t o b i hai tia c t nhauộ ạ ở ắ
b) Góc tù là góc l n h n góc vuôngớ ơ
c) N u Oz là tia phân giác c a thì ế ủ
d) N u thì Oz là tia phân giác c a ế ủ
e) Góc vuông là góc có s đo b ng ½ s đo c a góc b tố ằ ố ủ ẹ
f) Hai góc k nhau là hai góc có m t c nh chungề ộ ạ
g) Tam giác MNP là hình g m 3 đo n th ng MN : NP : MPồ ạ ẳ
h) M i đi m n m trên đng tròn đu cách tâm 1 kho ng b ng bán kínhọ ể ằ ườ ề ả ằ
Câu h i 4:ỏ Luy n v hìnhệ ề
+ V 2 góc ph nhauẽ ụ +V 2 góc k nhauẽ ề
+ V 2 góc k bùẽ ề +V góc ;;góc vuôngẽ
Nguy n Văn Quy n – 0938.59.6698 – s u t m và biên so nễ ề ư ầ ạ
+ V tam giác ABC bi t AB = 3cm; BC = 4cm, AC = 5cmẽ ế
+ V (O;5cm) và (O;3cm) c t nhau t i A và B.ẽ ắ ạ
Bài 1: Cho hai góc ;. Hai đi m B, C n m hai phía m t ph ng đi nhau có b là đng th ngể ằ ở ặ ẳ ố ờ ườ ẳ
OA. Ch ng minh ứ=.
Bài 2: Cho đi m B n m gi a 2 đi m A và C, đi m D n m gi a 2 đi m B và C, đi m O n mể ằ ữ ể ể ằ ữ ể ể ằ
ngoài đng th ng AC. Bi t r ng ;. Tính ?ườ ẳ ế ằ
Bài 3: Cho , v tia Oz sao cho ẽ
a) Tia Oz có xác đnh duy nh t hay không?ị ấ
b) Tính trong cùng tr ng h p?ườ ợ
Bài 4: Hai đng th ng AB và CD c t nhau O. Bi t r ng .Tính ,,?ườ ẳ ắ ở ế ằ
Bài 5: Trong m t n a m t ph ng có b ch a tia OH, xác đnh tia OI sao cho ,tia OK sao cho .ộ ử ặ ẳ ờ ứ ị
Tính ?
Bài 6: Tính s các góc A và góc B bi t chúng bù nhau và .ố ế
Bài 7: Hai đng th ng AB và CD c t nhau O. Bi t r ng . Tính s đo góc ườ ẳ ắ ở ế ằ ố
Bài 8: Cho hai tia Ox, Oy đi nhau. Trên cùng m t n a m t ph ng có b ch a tia Ox, v cácố ộ ử ặ ẳ ờ ứ ẽ
tia Oz, Ot sao cho .
a. Ch ng t r ng tia Oz n m gi a 2 tia Ox,Otứ ỏ ằ ằ ữ
b. Tính ?
c. Tính n u ().ế
Bài 9: Cho hai tia Ox, Oy đi nhau. Trên hai n a m t ph ng đi nhau có b ch a tia Ox v cácố ử ặ ẳ ố ờ ứ ẽ
tia Om, On sao cho . Ch ng t r ng Om, On là hai tia đi nhau.ứ ỏ ằ ố
Bài 10: Tính s đo các góc A và B bi t r ng chúng bù nhau và ố ế ằ
Bài 11: Cho góc vuông xOy, tia Oz n m gi a hai tia Ox, Oy. Tính bi t ằ ữ ế
Bài 12: Cho . G i Ox’ là tia đi c a tia Ox, Oy’ là tia đi c a tia Oy. Tính ọ ố ủ ố ủ
Bài 13: Cho đo n th ng BC = 5cm. Đi m D thu c tia BC sao cho BD = 3,5cm.ạ ẳ ể ộ
a. Tính đ dài DCộ
b. A là đi m n m ngoài đng th ng BC. K đo n th ng AD. Bi t . Tính ể ằ ườ ẳ ẻ ạ ẳ ế
Bài 14: Cho đi m M thu c đng th ng xy. L ý đi m B thu c tia xy sao cho MB = 3cm; MCể ộ ườ ẳ ấ ể ộ
= 2cm.
Nguy n Văn Quy n – 0938.59.6698 – s u t m và biên so nễ ề ư ầ ạ
a. Tính đ dài BCộ
b. G i O là m t đi m n m ngoài đng th ng BC. K đo n OM. Bi t Tính ọ ộ ể ằ ườ ẳ ẻ ạ ế
Bài 15: Cho tam giác ABC có BC = 5cm. Đi m M thu c tia đi c a tia CB sao cho CM = 3cm.ể ộ ố ủ
a. Tính đ dài BMộ
b. Cho bi t . Tính ế
c. Tính đ dài BK n u K thu c đo n th ng BM và CK = 1cmộ ế ộ ạ ẳ
Bài 16: Cho tam giác MON có ; OM = 4cm; ON = 3cm
a. Trên tia đi c a tia ON l y B sao cho OB = 2cm. Tính NBố ủ ấ
b. Trên n a m t ph ng ch a tia OM b là đng th ng ON, v tia OA sao cho. Tính ử ặ ẳ ứ ờ ườ ẳ ẽ