Trần Sĩ Tùng Giải tích 12
1
Chương I: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT
VÀ VẼ ĐỒ THỊ HÀM SỐ
Bài 1: BÀI TẬP SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
I. MỤC TIÊU:
Kiến thức:
Hiểu định nghĩa của sự đồng biến, nghịch biến của hàm số và mối liên hệ giữa khái
niệm này với đạo hàm.
Nắm được qui tắc xét tính đơn điệu của hàm số.
Kĩ năng:
Biết vận dụng qui tắc xét tính đơn điệu của một hàm số và dấu đạo hàm của nó.
Thái độ:
Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ
thống.
Giải tích 12 Trần Sĩ Tùng
2
II. CHUẨN BỊ:
Giáo viên: Giáo án. Hệ thống bài tập.
Học sinh: SGK, vở ghi. Ôn tập các kiến thức đã học về tính đơn điệu của hàm số.
III. HOẠT ĐỘNG DẠY HỌC:
1. Ổn định tổ chức: Kiểm tra sĩ số lớp.
2. Kiểm tra bài cũ: (Lồng vào quá trình luyện tập)
H.
Đ.
3. Giảng bài mới:
TL
Hoạt động của Giáo viên Hoạt động của Học sinh Nội dung
15'
Hoạt động 1: Xét tính đơn điệu của hàm số
H1. Nêu các bước xét tính
đơn điệu của hàm số?
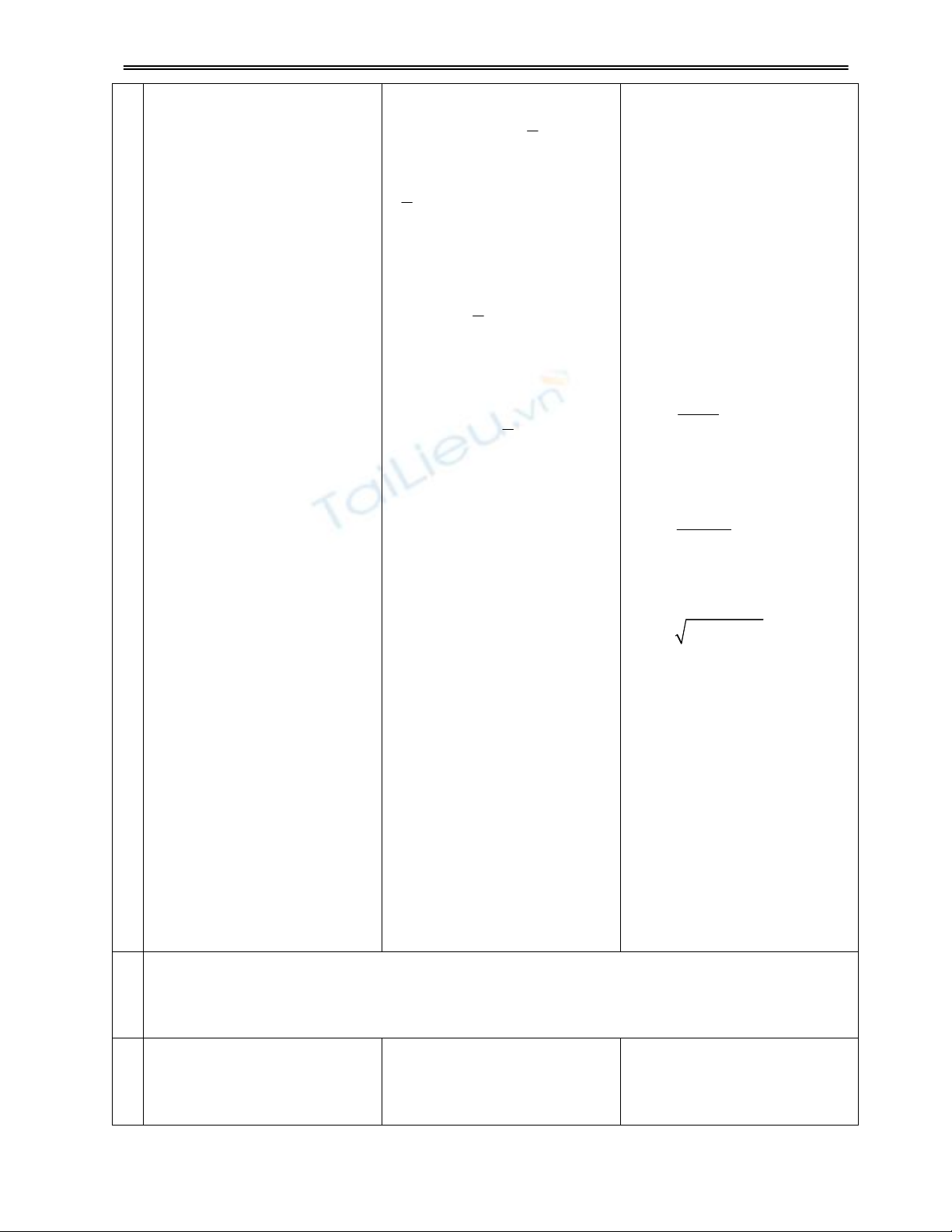
Đ1. 1. Xét sự đồng biến, nghịch
biến của hàm sô:
Trần Sĩ Tùng Giải tích 12
3
H2. Nhắc lại một số qui tắc
xét dấu đã biết?
a) ĐB:
3
2
;

, NB:
3
2;

b) ĐB:
2
0
3
,
NB:
0
;
 , 2
3;

c) ĐB:
1 0
;
,
1;

NB:
1
;

,
0 1
;
d) ĐB:
1 1; , ;
 
e) NB:
1 1; , ;
 
f) ĐB: 5
( ; )

, NB:
4
( ; )

a)
2
4 3
y x x
b) 3 2
5
y x x
c) 4 2
2 3
y x x
d)
3 1
1
x
y
x
e) 2
2
1
x x
y
x
f) 2
20
y x x
7' Hoạt động 2: Xét tính đơn điệu của hàm số trên một khoảng
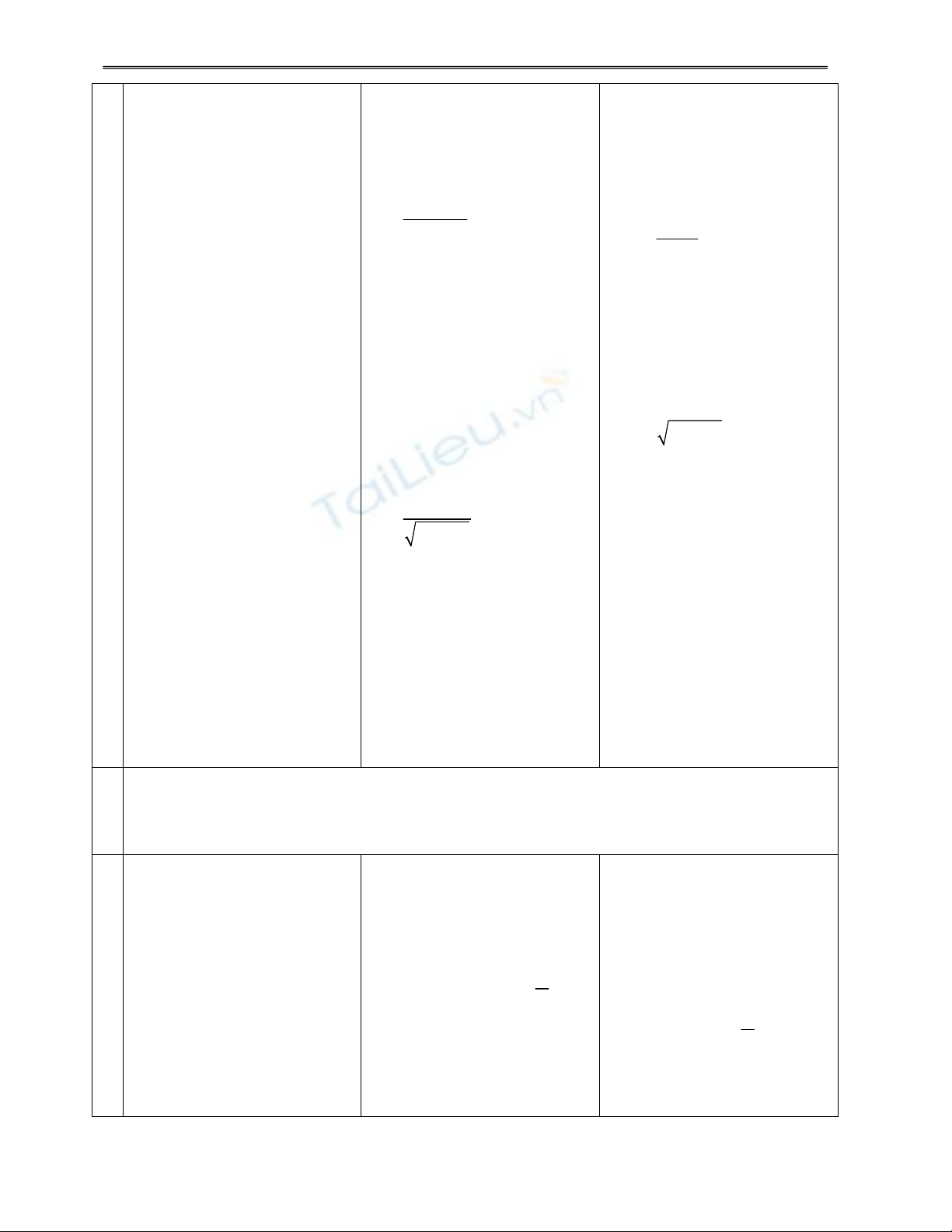
H1. Nêu các bước xét tính Đ1. 2. Chứng minh hàm số đồng
Giải tích 12 Trần Sĩ Tùng
4
đơn điệu của hàm số? a) D = R
2
2
2
1
1
x
y
x
'
y = 0 x = 1
b) D = [0; 2]
2
1
2
x
y
x x
'
y = 0 x = 1
biến, nghịch biến trên
khoảng được chỉ ra:
a) 2
1
x
y
x
, ĐB:
11
( ; )
,
NB: 1 1
( ; ),( ; )
 
b)
2
2
y x x
, ĐB:
0 1
( ; )
,
NB:
1 2
( ; )
15'
Hoạt động 3: Vận dụng tính đơn điệu của hàm số
GV hướng dẫn cách vận
dụng tính đơn điệu để chứng
minh bất đẳng thức.
– Xác lập hàm số.
a)
tan , 0;
2
y x x x .
3. Chứng minh các bất đẳng
thức sau:
a) tan 0
2
x x x .
Trần Sĩ Tùng Giải tích 12
5
– Xét tính đơn điệu của hàm
số trên miền thích hợp.
2
' tan 0, 0;
2
y x x
y = 0 x = 0
y đồng biến trên
0;
2
y(x) > y(0) với 0
2
x
b)
3
tan ; 0;
3 2
x
y x x x
2 2
' tan 0, 0;
2
y x x x
y = 0 x = 0
y đồng biến trên
0;
2
y(x) > y(0) với 0
2
x
b) 3
tan 0
3 2
x
x x x .