147
137. PH
Cho m
ộ
t
đồ
th
ị
vô h
ướ
ng G = (V, E) có n
đỉ
nh và m c
ạ
nh, không có
đỉ
nh cô l
ậ
p
Hãy chọn ra một tập ít nhất các cạnh để tất cả các đỉnh của đồ thị đều là đầu mút của ít nhất
một cạnh trong tập đã chọn !
Dữ liệu:
Vào t
ừ
file v
n b
ả
n COVER.INP
•
Dòng 1: Ch
ứ
a hai s
ố
n, m là s
ố
đỉ
nh và s
ố
c
ạ
nh c
ủ
a
đồ
th
ị
(1 ≤ n ≤ 100)
•
m dòng ti
ế
p theo, m
ỗ
i dòng ghi hai s
ố
u, v t
ươ
ng
ứ
ng v
ớ
i m
ộ
t c
ạ
nh (u, v) c
ủ
a
đồ
th
ị
Kết quả:
Ghi ra file v
n b
ả
n COVER.OUT
•
Dòng 1: Ghi s
ố
k là s
ố
c
ạ
nh
đượ
c ch
ọ
n
•
k dòng ti
ế
p theo, m
ỗ
i dòng ghi ch
ỉ
s
ố
hai
đỉ
nh
đầ
u mút c
ủ
a m
ộ
t c
ạ
nh
đượ
c ch
ọ
n
Chú thích nho nhỏ : Bài này sử dụng kiến thức không phổ biến ! Bởi vậy không có gì là khó
hiểu nếu như bạn không làm được !
Ví dụ:
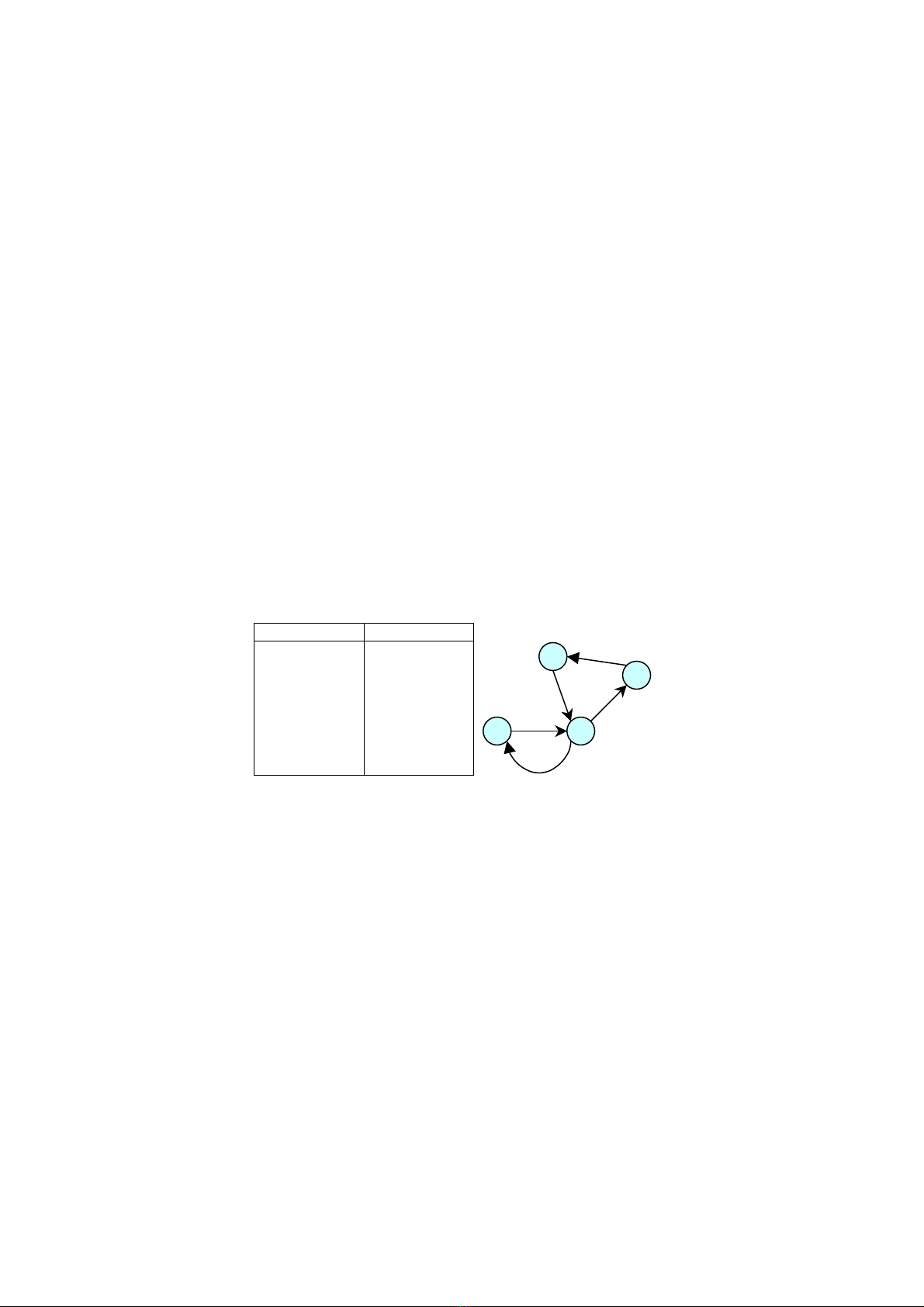
COVER.INP COVER.OUT
10 11
1 2
6 1
2 4
2 8
3 4
3 6
5 6
5 9
5 10
7 8
9 7
5
6 1
2 8
3 4
5 10
9 7
148
138. DI CHUYN RÔ-BT
Cho m
ộ
t
đồ
th
ị
có h
ướ
ng G g
ồ
m n
đỉ
nh và m cung, hai con Rô-b
ố
t
đứ
ng t
ạ
i hai
đỉ
nh nào
đ
ó.
Yêu cầu:
Chuyển nhanh nhất hai con Rô-bốt đến gặp nhau tại một đỉnh của đồ thị, biết rằng cả hai con
Rô-bốt chỉ đợc chạy theo các cung định hớng và không đợc dừng lại cho tới lúc gặp nhau tại
một đỉnh nào đó. Thời gian Rô-bốt đi qua một cung bất k+ luôn là 1 đơn vị thời gian
Dữ liệu:
Vào t
ừ
file v
n b
ả
n RMOVE.INP
•
Dòng 1: ch
ứ
a 4 s
ố
nguyên d
ươ
ng n, m, A, B.
Ở
đ
ây A và B l
ầ
n l
ượ
t là v
ị
trí c
ủ
a con rô-b
ố
t th
ứ
nh
ấ
t và v
ị
trí c
ủ
a con rô-b
ố
t th
ứ
hai, 2 ≤ n ≤ 250, 1 ≤ m ≤ 60000.
•
m dòng ti
ế
p theo, m
ỗ
i dòng ch
ứ
a hai s
ố
u, v t
ươ
ng
ứ
ng v
ớ
i m
ộ
t cung (u, v) c
ủ
a
đồ
th
ị
Kết quả:
Ghi ra file v
n b
ả
n RMOVE.OUT
•
Dòng 1: Ghi th
ờ
i gian tính t
ừ
lúc b
ắ
t
đầ
u di chuy
ể
n cho t
ớ
i lúc hai rô-b
ố
t g
ặ
p nhau
•
Dòng 2: Ghi hành trình c
ủ
a con rô-b
ố
t th
ứ
nh
ấ
t, theo
đ
úng th
ứ
t
ự
t
ừ
đỉ
nh A t
ớ
i
đỉ
nh g
ặ
p nhau
•
Dòng 3: Ghi hành trình c
ủ
a con rô-b
ố
t th
ứ
hai, theo
đ
úng th
ứ
t
ự
t
ừ
đỉ
nh B t
ớ
i
đỉ
nh g
ặ
p nhau
Các số trên một dòng của Input/Output file cách nhau ít nhất một dấu cách
Ràng buộc:
Luôn có ph
ươ
ng án th
ự
c hi
ệ
n yêu c
ầ
u trên
Giới hạn
: Ch
ươ
ng trình ch
ạ
y trên Turbo Pascal.
Ví dụ:
RMOVE.INP RMOVE.OUT
4 5 1 2
1 2
2 1
2 4
3 2
4 3
3
1 2 1 2
2 4 3 2
21
4
3
149
139. TRM NGH%
M
ộ
t toán k
ỵ
s
b
ỏ
ng
ự
a
đ
i thám hi
ể
m m
ộ
t khu r
ừ
ng và
đế
n khi tr
ờ
i t
ố
i, h
ọ
mu
ố
n
đ
i v
ề
nh
ữ
ng tr
ạ
m
ngh
ỉ
. R
ấ
t may là các k
ỵ
s
đề
u có b
ả
n
đồ
khu r
ừ
ng trong tay, nh
ờ
đ
ó có th
ể
xác
đị
nh chính xác v
ị
trí
c
ủ
a h
ọ
, các tr
ạ
m ngh
ỉ
, các khu v
ự
c có thú d
ữ
và t
ấ
t nhiên c
ả
v
ị
trí c
ủ
a các con ng
ự
a (n
ơ
i h
ọ
đ
ã b
ỏ
l
ạ
i).
M
ỗ
i k
ỵ
s
s
ẽ
ph
ả
i ch
ọ
n cho mình m
ộ
t con ng
ự
a, m
ộ
t tr
ạ
m ngh
ỉ
và dùng còi siêu âm g
ọ
i con ng
ự
a
đ
ó
v
ề
tr
ạ
m ngh
ỉ
đ
ã ch
ọ
n. M
ỗ
i tr
ạ
m ngh
ỉ
ch
ỉ
đủ
ch
ỗ
cho m
ộ
t k
ỵ
s
và m
ộ
t con ng
ự
a.
Giả sử rằng có m trạm nghỉ, n kỵ s, n con ngựa và bạn là một trong số những kỵ s đó. Hãy vạch
ra hành trình cho các kỵ s và các con ngựa để thời gian tính từ lúc bắt đầu cho tới khi tất cả các
con ngựa và các kỵ s về tới trạm nghỉ tơng ứng là nhỏ nhất.
B
ả
n
đồ
khu r
ừ
ng
đượ
c mã hoá b
ằ
ng m
ộ
t l
ướ
i ô vuông
đơ
n v
ị
kích th
ướ
c pxq. Trên m
ỗ
i ô ghi m
ộ
t
trong 5 ký hi
ệ
u:
•
"%":
Đị
a
đ
i
ể
m có thú d
ữ
•
".":
Đị
a
đ
i
ể
m an toàn (không có thú d
ữ
)
•
"&":
Đị
a
đ
i
ể
m an toàn có m
ộ
t con ng
ự
a
đ
ang
đứ
ng
•
"*":
Đị
a
đ
i
ể
m an toàn có m
ộ
t k
ỵ
s
đ
ang
đứ
ng
•
"@": Tr
ạ
m ngh
ỉ
V
ớ
i 1
đơ
n v
ị
th
ờ
i gian, m
ỗ
i k
ỵ
s
và m
ỗ
i con ng
ự
a có th
ể
th
ự
c hi
ệ
n m
ộ
t b
ướ
c
đ
i. Nhìn trên b
ả
n
đồ
,
m
ỗ
i b
ướ
c
đ
i c
ủ
a m
ộ
t k
ỵ
s
là m
ộ
t phép di chuy
ể
n t
ừ
ô
đ
ang
đứ
ng sang m
ộ
t trong các ô k
ề
c
ạ
nh,
b
ướ
c
đ
i này
đượ
c mã hoá b
ằ
ng m
ộ
t trong 4 ký hi
ệ
u {E, W, S, N}. M
ỗ
i b
ướ
c
đ
i c
ủ
a m
ộ
t con ng
ự
a là
m
ộ
t phép di chuy
ể
n nh
ư
m
ộ
t n
ướ
c
đ
i c
ủ
a quân mã theo lu
ậ
t c
ờ
, b
ướ
c
đ
i này
đượ
c mã hoá b
ằ
ng m
ộ
t
trong 8 ký hi
ệ
u {1, 2, 3, 4, 5, 6, 7, 8}. Các k
ỵ
s
c
ng nh
ư
các con ng
ự
a không
đượ
c
đ
i t
ớ
i ô có thú
d
ữ
hay
đ
i ra ngoài b
ả
n
đồ
. Các ký hi
ệ
u t
ươ
ng
ứ
ng v
ớ
i các h
ướ
ng
đ
i
đượ
c ch
ỉ
ra trong hình d
ướ
i
đ
ây:
6
7
N
5
8
W
*
E
&
S
4
1
3
2
Dữ liệu:
Vào t
ừ
file v
n b
ả
n HORSEMAN.INP
•
Dòng
đầ
u tiên: Ch
ứ
a hai s
ố
p, q cách nhau 1 d
ấ
u cách
•
p dòng ti
ế
p theo, dòng th
ứ
i ch
ứ
a q ký t
ự
, ký t
ự
th
ứ
j là ký hi
ệ
u ghi trên ô (i, j) c
ủ
a b
ả
n
đồ
Kết quả:
Ghi ra file v
n b
ả
n HORSEMAN.OUT
•
Dòng
đầ
u tiên: Ghi th
ờ
i gian nhanh nh
ấ
t
để
t
ấ
t c
ả
các k
ỵ
s
và các con ng
ự
a v
ề
t
ớ
i tr
ạ
m ngh
ỉ
t
ươ
ng
ứ
ng
•
2n dòng ti
ế
p theo, c
ứ
hai dòng ghi hành trình c
ủ
a m
ộ
t k
ỵ
s
:
♦
Dòng 1: Ghi hai s
ố
x, y cách nhau m
ộ
t d
ấ
u cách là v
ị
trí ô (x, y) c
ủ
a m
ộ
t k
ỵ
s
♦
Dòng 2: Ghi m
ộ
t dãy ký t
ự
t
ượ
ng tr
ư
ng cho m
ộ
t dãy các b
ướ
c
đ
i c
ủ
a k
ỵ
s
t
ừ
ô (x, y) theo
đ
úng th
ứ
t
ự
này
đế
n m
ộ
t tr
ạ
m ngh
ỉ
.
•
2n dòng ti
ế
p theo, c
ứ
hai dòng ghi hành trình c
ủ
a m
ộ
t con ng
ự
a:
♦
Dòng 1: Ghi hai s
ố
u, v cách nhau m
ộ
t d
ấ
u cách là v
ị
trí ô (u, v) c
ủ
a m
ộ
t con ng
ự
a
♦
Dòng 2: Ghi m
ộ
t dãy ký t
ự
t
ượ
ng tr
ư
ng cho m
ộ
t dãy các b
ướ
c
đ
i c
ủ
a con ng
ự
a t
ừ
ô (u, v)
theo
đ
úng th
ứ
t
ự
này
đế
n m
ộ
t tr
ạ
m ngh
ỉ
.
Ràng buộc:
•
5 ≤ p, q ≤ 100
•
1 ≤ n = s
ố
ô "&" = s
ố
ô "*" ≤ 100
•
n ≤ m = s
ố
ô "@" ≤ 100
•
Luôn luôn có ph
ươ
ng án th
ự
c hi
ệ
n yêu c
ầ
u c
ủ
a
đề
bài
150
Ví dụ:
( Kết quả file Output này sai ! ) Đáp án tối ưu phải là 3 mới đúng !
HORSEMAN.INP HORSEMAN.OUT
5 6
.&&.*.
.%%...
@@.@.@
&.....
*...*.
4
1 5
SSW
5 1
NN
5 5
NNE
1 2
3
1 3
2
4 1
1727
151
140. CHIA CÂN B!NG
Xét
đồ
th
ị
vô h
ướ
ng liên thông G = (V, E) có n
đỉ
nh và m c
ạ
nh, các
đỉ
nh
đượ
c
đ
ánh s
ố
t
ừ
1 t
ớ
i n
Hãy bỏ đi một số ít nhất các cạnh của đồ thị sao cho:
1.
Đồ
th
ị
còn l
ạ
i có
đ
úng 2 thành ph
ầ
n liên thông
2.
Đỉ
nh 1 và
đỉ
nh n không thu
ộ
c cùng m
ộ
t thành ph
ầ
n liên thông
3.
Trong các ph
ươ
ng án tho
ả
mãn c
ả
hai
đ
i
ề
u ki
ệ
n trên, hãy ch
ỉ
ra ph
ươ
ng án mà
độ
chênh l
ệ
ch v
ề
s
ố
đỉ
nh gi
ữ
a hai thành ph
ầ
n liên thông
đ
ó là nh
ỏ
nh
ấ
t
Dữ liệu:
Vào t
ừ
file v
n b
ả
n BALANCE.INP
•
Dòng 1: Ch
ứ
a hai s
ố
n, m (2 ≤ n ≤ 300)
•
m dòng ti
ế
p theo, m
ỗ
i dòng ch
ứ
a hai s
ố
u, v t
ươ
ng
ứ
ng v
ớ
i m
ộ
t c
ạ
nh (u, v) c
ủ
a
đồ
th
ị
Kết quả:
Ghi ra file v
n b
ả
n BALANCE.OUT
•
Dòng 1: Ghi s
ố
c
ạ
nh
đượ
c b
ỏ
(k)
•
k dòng ti
ế
p theo, m
ỗ
i dòng ghi hai
đỉ
nh t
ươ
ng
ứ
ng v
ớ
i m
ộ
t c
ạ
nh
đượ
c b
ỏ
Ví dụ:
BALANCE.INP BALANCE.OUT