ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 1
ĐỀ ÔN TẬP KIỂM TRA CUỐI HỌC KÌ I
MÔN: TOÁN 12 – ĐỀ SỐ: 14
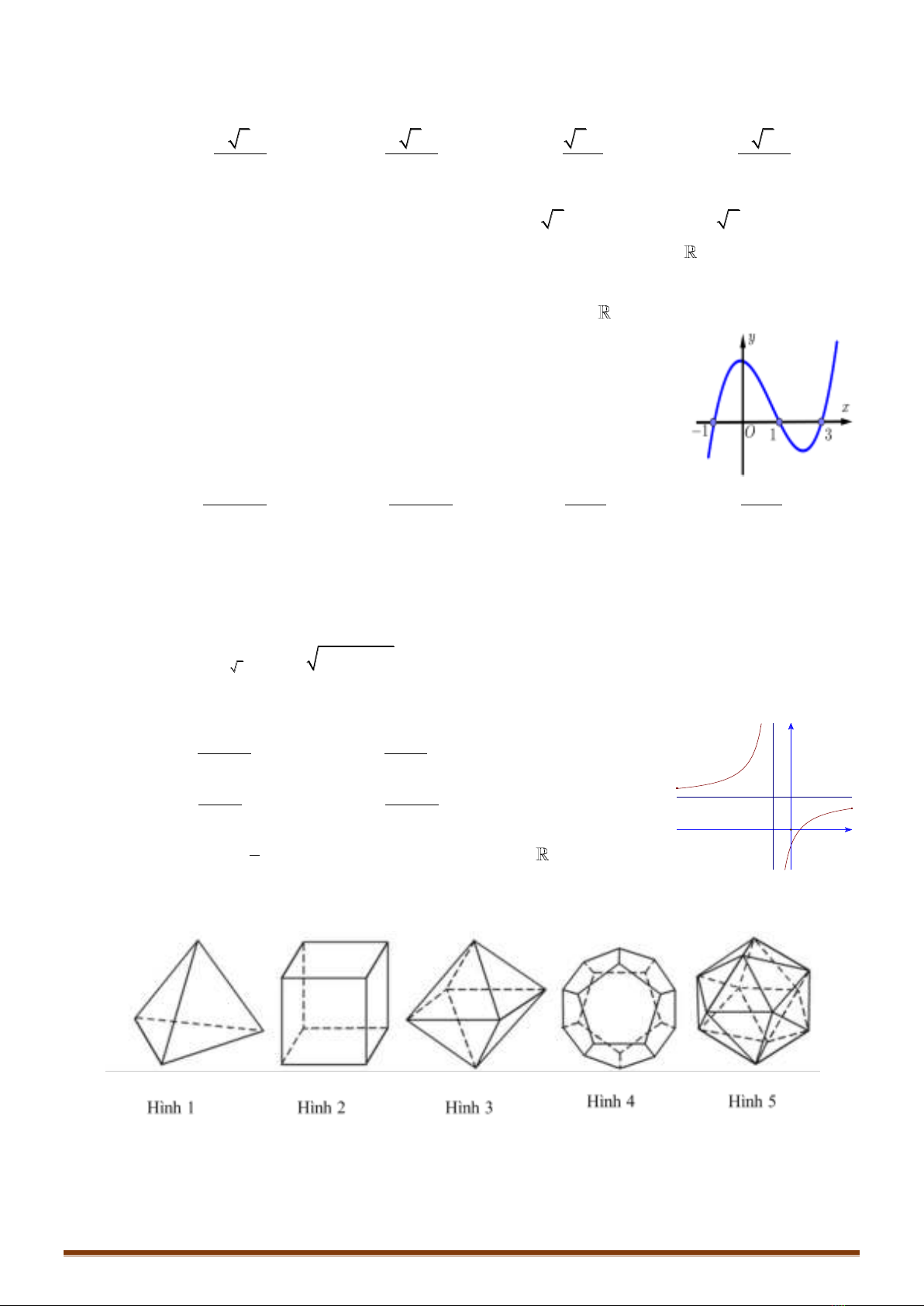
Câu 1: Số mặt đối xứng của lăng trụ tam giác đều là
A.
4
. B.
3
. C.
5
. D.
6
.
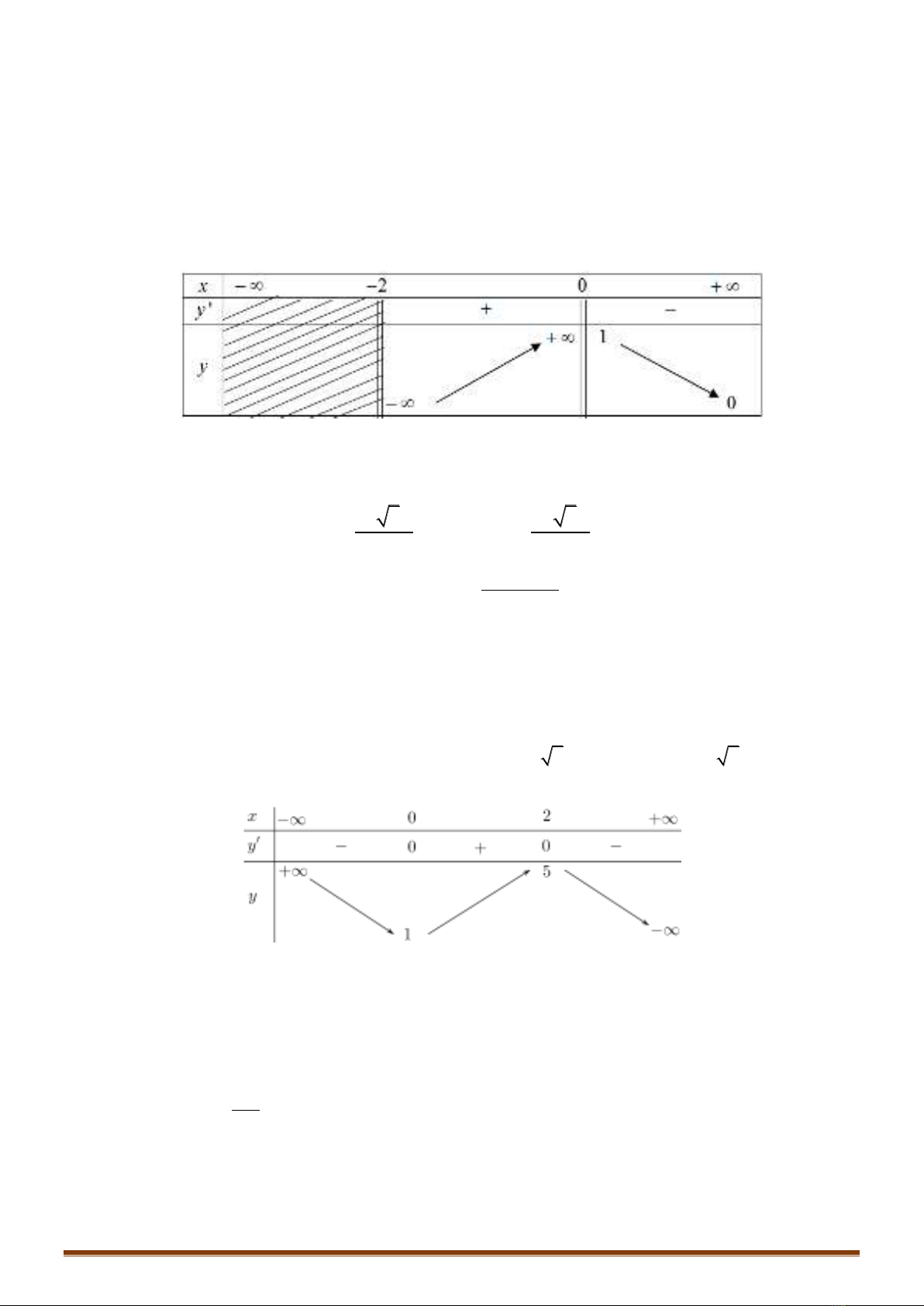
Câu 2: Cho hàm số
( )
y f x=
có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho
có bao nhiêu đường tiệm cận?
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 3: Cho hình nón có bán kính đáy bằng 4 và góc ở đỉnh bằng
0
60
. Diện tích xung quanh của hình
nón đã cho bằng
A.
64
. B.
32 3
3
. C.
64 3
3
. D.
.
Câu 4: Đường tiệm cận đứng của đồ thị hàm số
22
2
xx
yx
+−
=−
là:
A.
2x=
. B.
2x=−
. C.
2y=−
. D.
2y=
.
Câu 5: Cho hình hộp chữ nhật
.ABCD A B C D
có
4AB AD==
,
2AA=
. Gọi
O
là giao điểm
AC
và
BD
. Mặt cầu
( )
S
tâm
O
, bán kính
OA
cắt mặt phẳng
( )
A B C D
theo giao tuyến là đường tròn
( )
C
. Diện tích hình tròn
( )
C
bằng
A.
8
. B.
4
. C.
42
. D.
22
.
Câu 6: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Hàm số đạt cực đại tại điểm
A.
2x=
. B.
0x=
. C.
1x=
. D.
5x=
.
Câu 7: Tiếp tuyến của đồ thị hàm số
32
32y x x= − −
có hệ số góc
3k=−
có phương trình là
A.
31yx= − −
. B.
31yx= − +
. C.
39yx= − −
. D.
39yx= − +
.
Câu 8: Tìm giá trị lớn nhất của hàm số
32
8y x x x= − −
trên đoạn
[1;3]
.
A.
[1;3]
176
max 27
y=
. B.
[1;3]
max 8y=−
. C.
[1;3]
max 6y=−
. D.
[1;3]
max 4y=−
.
Câu 9: Phương trình
2
22
log 5log 4 0xx− + =
có hai nghiệm
12
,xx
. Tính tích
12
.xx
.
A.
8
. B.
32
. C.
16
. D.
36
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 2
Câu 10: Một khối nón có bán kính đáy
2ra=
và chiều cao
3ha=
. Hãy tính thể tích của nó.
A.
3
4Va
=
. B.
3
2Va
=
. C.
3
12Va
=
. D.
3
6Va
=
.
Câu 11: Với
, , 0abc
,
1a
,
, khẳng định sai là:
A.
( )
log . log log
a a a
b c b c=+
. B.
( )
log log .log
a a a
b c b c+=
.
C.
log log
aa
bb
=
. D.
log log log
a a a
bbc
c=−
.
Câu 12: Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
A
,
AC a=
,
2BC a=
. Hình chiếu vuông
góc của
S
trên
( )
ABC
là trung điểm
H
của
BC
. Cạnh
SB
tạo với đáy một góc
0
60
. Tính thể
tích
V
khối chóp
.S ABC
A.
3
2
a
V=
. B.
33
5
a
V=
. C.
33
12
a
V=
. D.
3
6
a
V=
.
Câu 13: Cho khối lập phương có cạnh bằng
a
.Thể tích của khối lập phương đã cho bằng
A.
2
a
. B.
3a
. C.
3
a
. D. 4
2
a
.
Câu 14: Tập xác định
D
của hàm số
2
log 2yx=−
là
A.
( )
2;D= +
. B.
DR=
.
C.
( ) ( )
;1 2;D= − +
. D.
\2D=
.
Câu 15: Với
a
là số thực dương tùy ý,
7
2
log a
bằng
A.
2
7log a
. B.
2
1log
7a
. C.
2
1log
7a+
. D.
2
7 log a+
.
Câu 16: Đồ thị hàm số
2
2
x
yx
=+
có bao nhiêu tiệm cận ngang?
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 17: Cho hàm số có đồ thị như hình vẽ dưới đây. Số điểm cực trị của hàm số đã cho là:
A. 1. B. 3. C. 0. D. 2.
Câu 18: Cho hàm số
( )
y f x=
xác định, liên tục trên và có đạo hàm
( )
fx
. Biết rằng
( )
fx
có đồ
thị như hình vẽ dưới đây. Mệnh đề nào sau đây đúng
A. Hàm số
( )
y f x=
nghịch biến trên khoảng
( )
0; +
.
B. Hàm số
( )
y f x=
nghịch biến trên khoảng
( )
3;2−
.
C. Hàm số
( )
y f x=
đồng biến trên khoảng
( )
;3−
.
D. Hàm số
( )
y f x=
đồng biến trên khoảng
( )
2;0−
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 3
Câu 19: Cho hàm số
( )
=y f x
có bảng biến thiên như hình đã cho:
Số nghiệm của phương trình
( )
2 5 0fx+=
A.
1
. B.
4
. C.
3
. D.
2
.
Câu 20: Thể tích của khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng
a
bằng:
A.
3
3
a
. B.
32
3
a
. C.
33
4
a
. D.
33
6
a
.
Câu 21: Hình trụ tròn xoay
( )
T
có diện tích xung quanh
2
12
xq
Sa
=
và chiều cao của khối trụ là
6ha=
. Thể tích khối trụ tương ứng bằng
A.
3
2Va
=
. B.
3
12Va
=
. C.
3
6Va
=
. D.
3
3Va
=
.
Câu 22: Cho hàm số
42
y ax bx c= + +
có đồ thị như hình vẽ sau. Trong các mệnh đề dưới đây, mệnh đề
nào đúng?
A.
0, 0, 0a b c
. B.
0, 0, 0abc
. C.
0, 0, 0a b c
. D.
0, 0, 0a b c
.
Câu 23: Cho các số thực
;xy
thỏa mãn
1.xy
Tìm giá trị nhỏ nhất
min
P
của biểu thức
23
log 36log .
xy
y
x
Px y
=+
A.
min 23.P=
B.
min 27.P=
C.
min 32.P=
D.
min 72.P=
Câu 24: Cho lăng trụ
' ' '
.ABC A B C
có đáy là tam giác vuông cân tại
B
,
3.AB a=
Hình chiếu vuông
góc của
'
A
lên mặt phẳng
()ABC
là điểm
H
thuộc cạnh AC sao cho
2HC HA=
. Mặt bên
''
()ABB A
tạo với đáy một góc
0
60
. Thể tích khối lăng trụ là
A.
3
3
2
a
. B.
3
3
5
a
. C.
3
3
a
. D.
3
6
a
.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 4
Câu 25: Tập nghiệm của phương trình
( )
2
5
log 2 1 1xx− − =
là:
A.
3
2; 2

−


. B.
{2}
. C.
3
2; 2

−


. D.
.
Câu 26: Diện tích toàn phần của hình trụ có bán kính đáy
R
và độ dài đường sinh
l
là:
A.
2
2
tp
S R Rl

=+
. B.
2
tp
S R Rl

=+
. C.
2
22
tp
S R Rl

=+
. D.
22
tp
S R Rl

=+
.
Câu 27: Đồ thị sau là của hàm số nào?
A.
1
2
x
y
=

. B.
2x
y=
.
C.
2
logyx=
. D.
( )
2
log 3x+
.
Câu 28: Tìm tất cả các giá trị thực của
m
để phương trình
9 4.3 2 0
xx
m− + − =
có hai nghiệm phân biệt.
A.
26m
. B.
36m
.
C.
06m
. D.
6m
.
Câu 29: Cho hình trụ có bán kính đáy bằng 4, độ dài đường sinh
bằng 12. Tính diện tích xung quanh
xq
S
của hình trụ.
A.
192
xq
S
=
. B.
48
xq
S
=
. C.
128
xq
S
=
. D.
96
xq
S
=
.
Câu 30: Độ dài đường cao của khối tứ diện đều cạnh
là
A.
6a
. B.
2a
. C.
. D.
.
Câu 31: Cho khối chóp có diện tích đáy
2
12cm
và chiều cao
. Thể tích của khối chóp bằng
A.
3
22cm
. B.
3
26cm
. C.
3
24cm
. D.
3
28cm
.
Câu 32: Cho hàm số
( )
y f x=
có bảng biến thiên như sau
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A.
( )
;3−
. B.
( )
2;6
. C.
( )
1; +
. D.
( )
1;3
.
Câu 33: Tìm các giá trị của tham số m để hàm số
( ) ( )
32
11
1 3 2
36
y mx m x m x= − − + − +
đạt cực trị tại
12
,xx
thỏa mãn
12
21xx+=
.
A.
2
3
2
m
m
=
=
. B.
66
11
22
m− +
.
C.
66
1 ;1 \ 0
22
m
− +



. D.
2m=
.
Câu 34: Có bao nhiêu giá trị nguyên của tham số m để phương trình
33 2 0x x m− + − =
có 3 nghiệm phân
biệt?
A.
3
. B.
2
. C.
1
. D. Vô số.
ĐỀ ÔN TẬP KIỂM TRA CUỐI HKI – TOÁN 12
Page 5
Câu 35: Cho tứ diện đều
ABCD
có cạnh bằng
a
. Hình nón
()N
có đỉnh
A
và đường tròn đáy là đường
tròn ngoại tiếp tam giác
BCD
. Tính thể tích
V
của khối nón
()N
.
A.
3
3
27
a
V
=
. B.
3
6
27
a
V
=
. C.
3
6
27
a
V=
. D.
3
6
9
a
V
=
.
Câu 36: Một mặt cầu có diện tích
16
thì bán kính mặt cầu bằng
A. 2. B. 4. C.
42
. D.
22
.
Câu 37: Tìm tất cả các giá trị của
a
để hàm số
( )
2020 x
ya=−
nghịch biến trên .
A.
0 1.a
B.
2019 2020.a
C.
2020.a
D.
2019.a
Câu 38: Cho hàm số
( )
fx
có đạo hàm
( )
'fx
xác định, liên tục trên và
( )
'fx
có đồ thị như hình vẽ.
Số điểm cực trị của hàm số
( )
x
y f xe=
bằng
A.
3.
B.
1.
C.
4.
D.
2.
Câu 39: Đạo hàm của hàm số
( )
2
ln 1yx=+
bằng
A.
( )
2
2
1
'1
y
x
=+
. B.
( )
2
2
1
'1
y
x
−
=+
. C.
2
2
'1
x
yx
=+
. D.
2
1
'1
yx
=+
.
Câu 40: Tập nghiệm của bất phương trình
7 49
x
là
A.
( )
;2−
. B.
( )
0;2
. C.
( )
;7−
. D.
( )
2; +
.
Câu 41: Gọi
S
là tập các số nguyên
2020;2020m−
để phương trình
2
22
2
log log logx x m m x− = − +
có đúng hai nghiệm. Số phần tử của
S
bằng
A.
1
. B.
2020
. C.
2021
. D.
0
.
Câu 42: Hình vẽ dưới là đồ thị của hàm số nào sau đây?
A.
21
1
x
yx
−+
=+
. B.
21
1
x
yx
−
=+
.
C.
21
1
x
yx
+
=−
. D.
21
1
x
yx
−+
=−
.
Câu 43: Hàm số
32
1
3
y mx mx x= − + −
luôn nghịch biến trên khi và chỉ khi
A.
1m−
. B.
01m
. C.
0m
. D.
0m
hoặc
1m
.
Câu 44: Trong các khối đa diện đều dưới đây, hình nào là khối bát diện đều?
A. Hình 1. B. Hình 2. C. Hình 4. D. Hình 3.
x
y
-
1
2
O