GV: Lê Tin Dũng. B môn TðH_Khoa ðin.
7
Ch−¬ng2
Ch−¬ng2Ch−¬ng2
Ch−¬ng2








2.1 Cu to và nguyên lý hot ñng ca ñng cơ ñin mt chiu
Nh−chóngta®biÕttrongvËtlý,khi®Ætvotrongtõtr−êngmétd©ydÉnvchodßng®iÖn
ch¹yquad©ydÉnth×tõtr−êngsÏt¸cdôngméttõlùcvodßng®iÖn(chÝnhlvod©ydÉn)vlm
d©ydÉnchuyÓn®éng.ChiÒucñatõlùcx¸c®Þnhtheoquyt¾cbntaytr¸i.
§éngc¬®iÖnnãichungv®éngc¬®iÖnmétchiÒunãiriªngho¹t®éngtheonguyªnt¾cny.
 
 
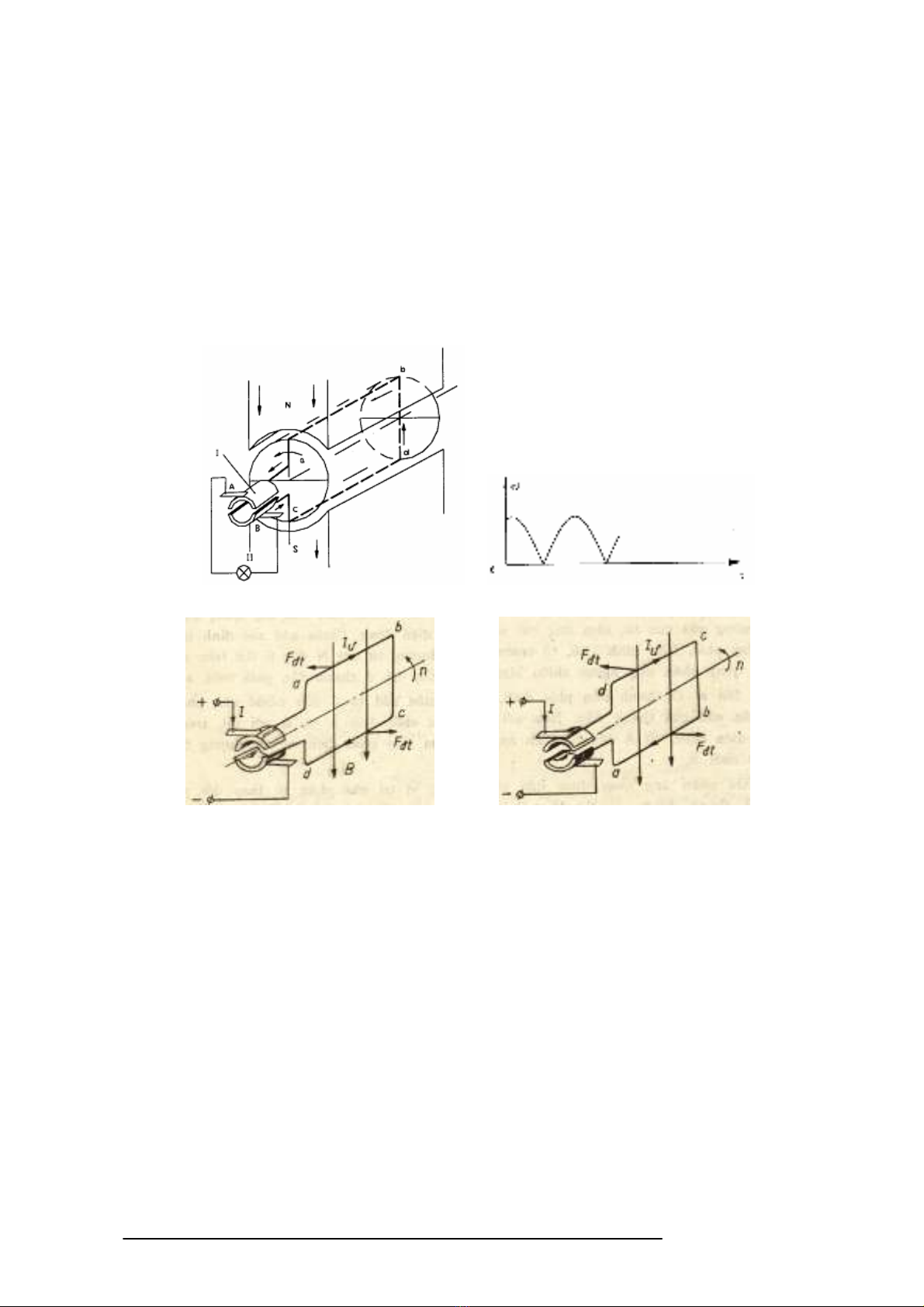
Trên hình 2.1 là sơ ñ nguyên lý hot ñng ca ñng cơ ñin mt chiu. Nó gm mt khung
dây abcd hai ñu ni vi 2 phin góp, ñt trong t trưng ca nam châm vĩnh cu N-S, hai chi
ñin A và B ñt c ñnh và tỳ sát lên trên 2 phin góp.
Ti thi ñim như hình c), v trí thanh dn ab nm na trên ca trc quay, dòng ñin t
mch ngoài qua chi than chy trong thanh dn ab có chiu t a ñn b và lc ñin t F
ñt
xác ñnh
theo quy tc bàn tay trái hưng vuông góc vi ab như hình v. V trí thanh dn cd nm na dưi
ca trc quay, dòng ñin trong thanh dn cd hưng t c ñn d và lc ñin t F
ñt
như hình v. Cp
lc ñin t trong hai thanh dn ab và cd này to thành ngu lc, to ra mômen làm khung dây quay.
Khi khung dây quay ñưc ½ vòng, ti thi ñim như hình d), lúc này v trí ca thanh dn cd
nm na trên ca trc quay, nh có c góp và chi than nên chiu ca dòng ñin qua thanh dn cd
ño chiu chy t d ñn c, lc ñin t F
ñt
tác dng lên thanh dn cd ño chiu so vi na chu kỳ
trưc ñó. Tương t, v trí ca thanh dn ab lúc này nm na dưi ca trc quay, dòng ñin chy
a)
b)
c)
d)
Hình 2.1 - Nguyên lý hot ñng ca ñng cơ ñin mt chiu.
GV: Lê Tin Dũng. B môn TðH_Khoa ðin.
8
t b ñn a và ñin t F
ñt
tác dng lên thanh dn ab cũng ño chiu. Cp lc F
ñt
to ra mômen làm
khung dây vn tip tc quay theo chiu cũ.
Như v!y, nh có chi than và c góp ñin nên khi v trí ca khung dây thay ñi thì chiu dòng
ñin trong các thanh dn cũng thay ñi ñ chiu ca mômen ñin t tác dng lên khung dây không
ñi, ñm bo cho khung dây vn quay theo mt chiu xác ñnh.
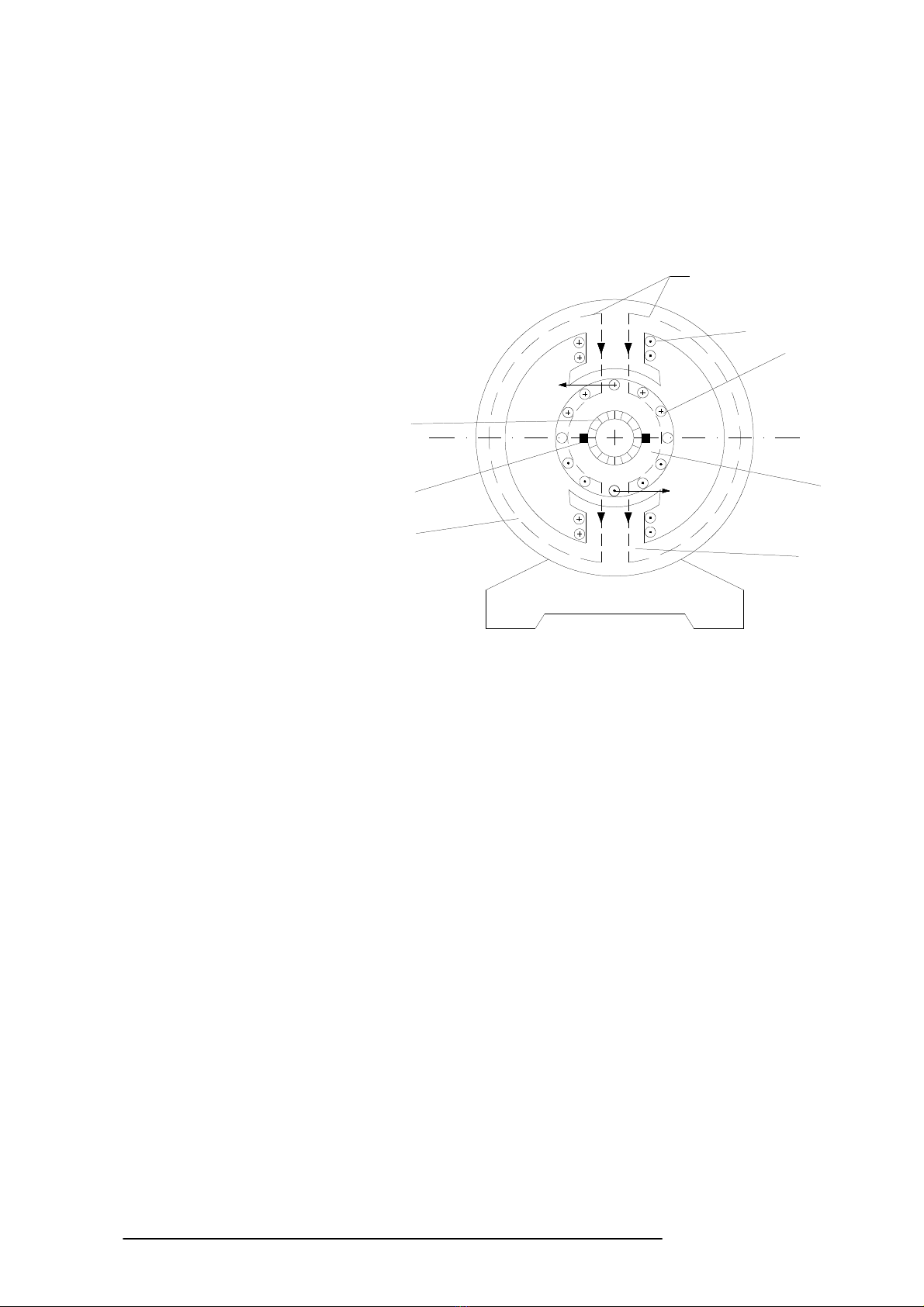
Ta xét c"u to ca ñng cơ ñin mt chiu như hình v.
φ

C"u to ca ñng cơ ñin mt chiu gm 2 phn chính: Phn mch kích t (to ra t trưng) và
phn quay (rôto).
T trưng ñưc to ra nh các cun dây 5 có dòng ñin mt chiu chy qua. Các cun này g#i
là cun dây kích t và ñưc qu"n quanh các cc t 4. Trưng hp như hình v, stato 6 ca ñng
cơ có ñt các cun dây kích t nên stato còn g#i là phn kích t (hay phn cm). T trưng do phn
kích t to ra s tác dng mt t lc vào các dây dn 7 ñt trong các rãnh ca Rôto 3 khi có dòng
ñin chy qua. Cun dây ñt trong các rãnh ca Rôto g#i là cun dây phn $ng. Dòng ñin ñưa vào
cun dây phn $ng qua các chi than 2 và c góp 1. Rôto mang cun dây phn $ng nên còn g#i là
phn $ng.
Căn c$ theo cách kích t cho ñng cơ ñin mt chiu, ngưi ta phân loi ñng cơ ñin mt
chiu ra làm các loi:
+ ðng cơ ñin mt chiu kích t ñc l!p.
+ ðng cơ ñin mt chiu kích t song song.
+ ðng cơ ñin mt chiu kích t ni tip.
+ ðng cơ ñin mt chiu kích t h'n hp.
1- C góp ñin.
2- Chi than.
3- Rotor.
4- Cc t.
5- Cun dây kích t.
6- Stato.
7- Cun dây phn $ng.
Hình 2.2 - C"u to ca ñng
cơ ñin mt chiu.
GV: Lê Tin Dũng. B môn TðH_Khoa ðin.
9
2.2§éngc¬®iÖnmétchiÒukÝchtõ®éclËpvkÝchtõsongsong
2.2.1Ph−¬ngtr×nh®ÆctÝnhc¬ ch ñ xác lp
§éngc¬®iÖnmétchiÒukÝchtõ®éclËp:CuénkÝchtõ®−îccÊp®iÖntõnguånmétchiÒu®éc
lËpvíinguån®iÖncÊpchor«to.
NÕucuénkÝchtõvcuénd©yphÇnøng®−îccÊp®iÖnbëicïngmétnguån®iÖnth×®éngc¬l
lo¹ikÝchtõsongsong.Tr−ênghîpnynÕunguån®iÖncãc«ngsuÊtrÊtlínsovíic«ngsuÊt®éng
c¬th×tÝnhchÊt®éngc¬sÏt−¬ngtùnh−®éngc¬kÝchtõ®éclËp.
Khi®éngc¬lmviÖc,r«tomangcuénd©yphÇnøngquaytrongtõtr−êngcñacuénc¶mnªn
trongcuénøngxuÊthiÖnmétsøc®iÖn®éngc¶møngcãchiÒung−îcvíi®iÖn¸p®ÆtvophÇnøng
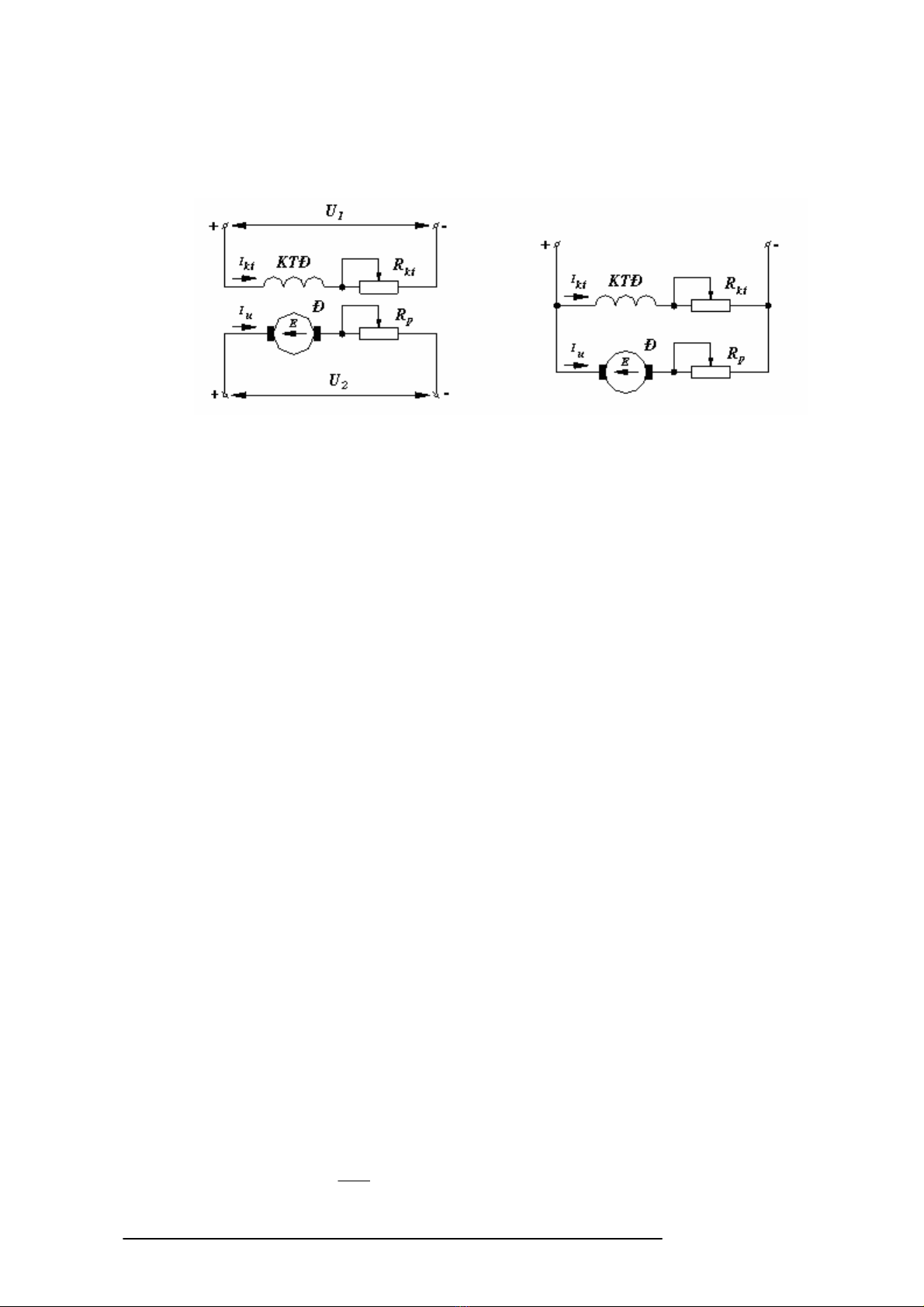
®éngc¬.Theos¬®ånguyªnlýtrªnh×nh2.3vh×nh2.4,cãthÓviÕtph−¬ngtr×nhc©nb»ng®iÖn¸p
cñam¹chphÇnøng(r«to)nh−sau:
U−=E−+(R−+Rp).I− (2.1)
Trong®ã:
VU−(V)l®iÖn¸pphÇnøng®éngc¬.
VE−(V)lsøc®iÖn®éngphÇnøng®éngc¬.
VR−(Ω)l®iÖntrëphÇnøngca ñng cơ.
VRp(Ω)l®iÖntrëphôni thêm vào m¹chphÇnøngñng cơ.
VI−ldßng®iÖnphÇnøng®éngc¬.
R−=r−+rct+rcb+rcp(2.2)
 r−V§iÖntrëcuénd©yphÇnøng.
rctV§iÖntrëtiÕpxócgi÷achæithanvphiÕngãp.
 rcbV§iÖntrëcuénbï.
 rcpV§iÖntrëcuéncùctõphô.
Søc®iÖn®éngphÇnøngtûlÖvíitèc®équaycñar«to:
E−=p. N
2πφ ω φ ω
aK⋅ ⋅ = ⋅ (2.3)
Hình 2.3 - Sơ ñ nguyên lý ñng
cơ ñin mt chiu kích t ñc l!p.
Hình 2.4 - Sơ ñ nguyên lý ñng
cơ ñin mt chiu kích t song song.
GV: Lê Tin Dũng. B môn TðH_Khoa ðin.
10
Kp N
a
=.
2πlhÖsèkÕtcÊucña®éngc¬.
φVTõth«ngquamçicùctõ.
pVSè®«icùctõchÝnh.
NVSèthanhdÉnt¸cdôngcñacuénøng.
aVSè®«im¹chnh¸nhsongsongcñacuénd©yphÇnøng.
HoÆctacãthÓviÕt: 
E−=Keφ.n(2.4)
V: ωπ
= =
2
60 9 55
n n
,
VËy: Ke=K/9,55=0,105K
Nhêlùctõtr−êngt¸cdôngvod©ydÉnphÇnøngkhicãdßng®iÖn,r«toquayd−íit¸cdông
cñam«men®iÖntõ:
M®t=K.φ.I−(2.5)
TõhÖ2ph−¬ngtr×nh(2.1)v(2.3)tacãthÓrótra®−îcph−¬ngtr×nh®ÆctÝnhc¬®iÖnbiÓuthÞ
mèiquanhÖω=f(I)cña®éngc¬®iÖnmétchiÒukÝchtõ®éclËpnh−sau:
 
−
−
−
I
K
RR
K
U
p
φφ
ω
+
−=  (2.6)
Tõph−¬ngtr×nh(2.5)rótraI−thayvoph−¬ngtr×nh(2.6)ta®−îc:
dt
pu
uM
K
RR
K
U
2
)(
φ
φ
ω
+
−= (2.7)
NÕubáquac¸ctænthÊtc¬vtænthÊtthÐpth×m«menc¬trªntrôc®éngc¬b»ngm«men®iÖn
tõ,takýhiÖulM.NghÜal:Mc¬=M®t=M.
Tacãph−¬ngtr×nh®ÆctÝnhc¬biÓuthÞmèiquanhÖω=f(M)cña®éngc¬®iÖnmétchiÒu
kÝchtõ®éclËpnh−sau:
 M
K
RR
K
U
p
2
)(
−
−
φ
φ
ω
+
−= (2.8)
CãthÓbiÓudiÔn®ÆctÝnhc¬d−íid¹ngkh¸c:
ω=ω0V∆ω (2.9)
Trong®ã:
ωφ
0
=U
K
−
gäiltèc®ékh«ngt¶ilýt−ëng.

M
K
RR
p
2
)(
−
φ
ω
+
=∆
gäil®ésôttèc®é
GV: Lê Tin Dũng. B môn TðH_Khoa ðin.
11
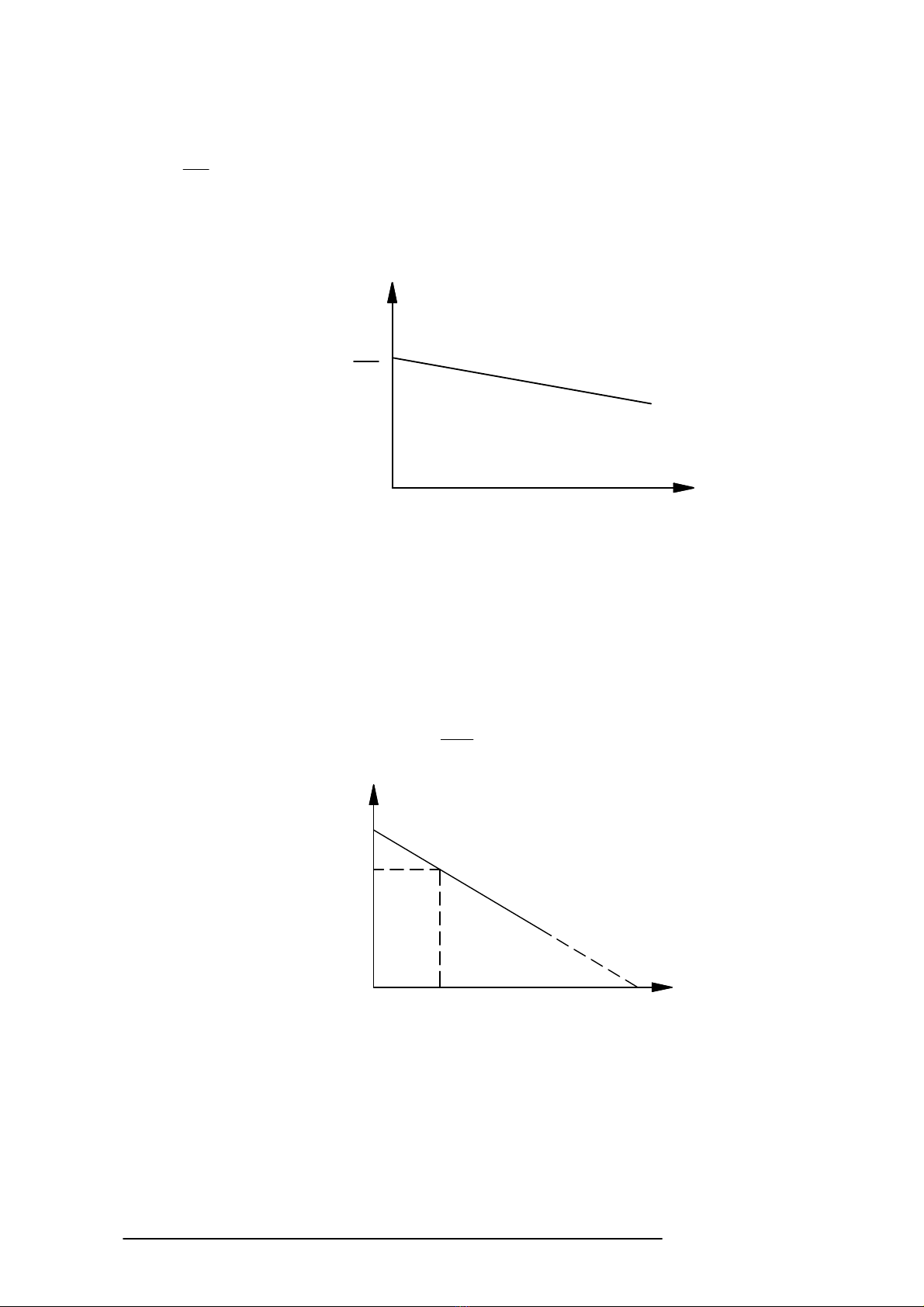
Ph−¬ngtr×nh®ÆctÝnhc¬(2.8)cãd¹nghmbËcnhÊty=B+Ax,nªn®−êngbiÓudiÔntrªnhÖ
täa®éM0ωlmét®−êngth¼ngvíi®édèc©m.§−êng®ÆctÝnhc¬c¾ttrôctung0ωt¹i®iÓmcãtung
®é: ωφ
0
=U
K
−
.Tèc®éω
0
®−îcgäiltèc®ékh«ngt¶ilýt−ëngkhikh«ngcãlùcc¶nnoc¶.§ãl
tèc®élínnhÊtcña®éngc¬m
thc t kh«ngthÓ®¹t®−îcëchÕ®é®éngc¬v×kh«ngbaogiêx¶y
ratr−ênghîpMC=0.
ω
0M
ω =
U
K.φ
ο
Khiphôt¶it¨ngdÇntõMC=0®ÕnMC=M®mth×tèc®é®éngc¬gi¶mdÇntõω0®Õnω®m.
§iÓmA(M®m,ω®m)gäil®iÓm®Þnhmøc.
Rârng®−êng®ÆctÝnhc¬cãthÓvÏ®−îctõ2®iÓmω0vA.§iÓmc¾tcña®ÆctÝnhc¬víitrôc
honh0Mcãtung®éω=0vcãhonh®ésuytõph−¬ngtr×nh(2.7):
M=Mnm=Kφ®m
−
R
U
dm
=Kφ®m.Inm (2.9)
o
M
0
ω
ω
A
ω
®m
M
®m
M
nm
M«menMnmvInmgäilm«menng¾nm¹chvdßng®iÖnng¾nm¹ch.§ãlgi¸trÞm«men
línnhÊtvdßng®iÖnlínnhÊtcña®éngc¬khi®−îccÊp®iÖn®Çy®ñmtèc®éb»ng0.Tr−ênghîp
nyx¶yrakhib¾t®Çumëm¸yvkhi®éngc¬®angch¹ymbÞdõngl¹iv×bÞkÑthoÆct¶ilínqu¸
kÐokh«ng®−îc.Dßng®iÖnInmnylínvth−êngb»ng:

V§ÆctÝnhc¬cña®éngc¬®iÖnmétchiÒukÝch
tõ®éclËp

V§ÆctÝnhc¬tùnhiªncña®éngc¬
®iÖnmétchiÒukÝchtõ®éclËp