
trungtrancbspkt@gmail.com biquyetthanhcong.net
Chuyên đề I: Ứng Dụng Đạo Hàm Trong Các Bài Toán Đại Số
I.Các vài toán liên quan đến nghiệm của pt-bpt:
Định lí 1: Số nghiệm của pt f(x)=g(x) chính là số giao điểm của hai đồ thị y=f(x) và
y=g(x)
Định lí 2: Nếu hàm số y=f(x) lt trên D và
min ( )
xD
m f x
,
ax ( )
xD
M M f x
thì pt: f(x)=k có
nghiệm khi và chỉ khi
m k M
Định lí 3: Bất phương trình
( ) ( )f x g x
nghiệm đúng mọi x thuộc D khi và chỉ khi
( ) ( )
x D x D
Min f x Max g x
Các ví dụ:
Bài 1:Tìm m để pt sau có nghiệm:
22
11x x x x m
(HSG Nghệ an 2005)
Lời giải: Xét hàm số
22
( ) 1 1f x x x x x
có tập xác định là D=R
22
22
22
22
2 1 2 1
'( ) ' 0
2 1 2 1
(2 1) 1 2 1 1 (1)
1 1 3 1 1 3
[( - ) ] [( ) ] 0 thay vaøo (1)ta thaáy khoâng
2 2 4 2 2 4
thoûa maõn. Vaäy f'(x)=0 voâ nghieäm, maø f'(0)=1>0, do
xx
f x f x
x x x x
x x x x x x
x x x x x
22
x+
x+
ñoù f'(x)>0 x
2
Maët khaùc: Lim ( ) = Lim 1; Lim ( ) 1
11
Vaäy pt ñaõ cho coù nghieäm -1 1
x
R
x
f x f x
x x x x
m
Bài 2:Tìm tất cả các giá trị của a để pt:
21 cosax x
có đúng một nghiệm
0; 2
x
(Đề thi HSG tỉnh Hải Dương Lớp 12 năm 2005)
Giải: Ta thấy để pt có nghiệm thì
0a
2
22
22
sin
cos 1 sin
2
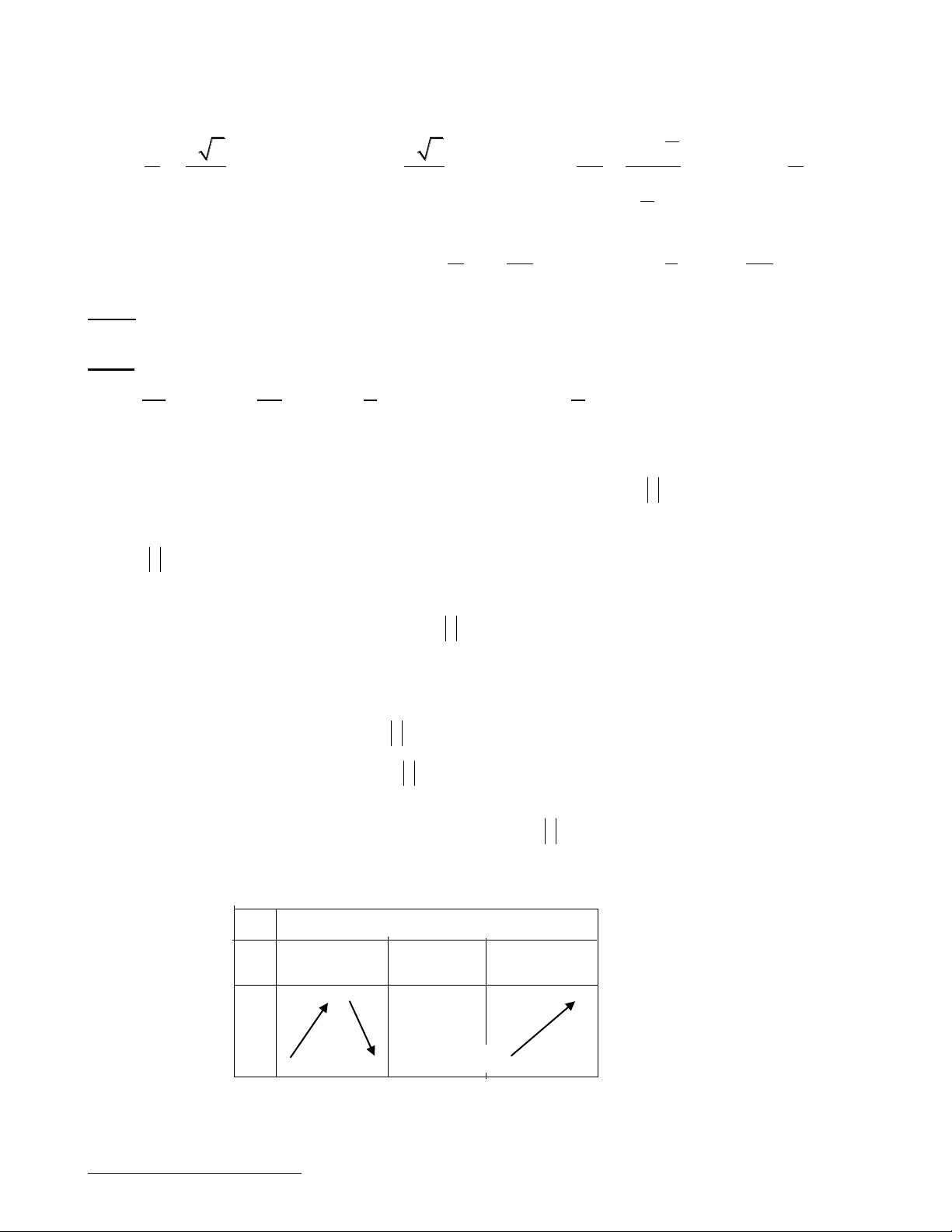
Khi ñoù pt =a -2 . Xeùt haøm soá ( ) vôùi t 0; 4
2
cos -
.cos sin
ta coù '( ) = 0 vôùi t 0; ( ) ngb treân 0;
44
t
x
xt
a f t t
xx
t t tgt
t t t
f t f t
t
trungtrancbspkt@gmail.com biquyetthanhcong.net
2
22
0
22
sin
2 2 2 2 8 2
Maø f( )= vaø ( ) 1 ( ) 1 1 (0; )
42
2
8 1 4
Vaäy pt ñaõ cho coù ñuùng 1 nghieäm (0; ) 21
22
t
x
Lim f t f t x
x
x a a
Bài 3: Cho phương trình
6 5 4 3 2
3 6 ax 6 3 1 0x x x x x
. Tìm tất cả các giá trị
của tham số a, để phương trình có đúng 2 nghiệm phân biệt. (HSG Nam Định 2004)
Giải: Vì
0x
không phải là nghiệm pt. Chia hai vế pt cho x3 ta được
32
32
2 2 3 2
22
1 1 1 1
( ) 3( ) 6( ) a=0 (1). Ñaët t= ta thu ñöôïc pt
( 3) 3( 2) 6 3 9 6 (1')
Töø caùch ñaët t ta coù: 1 0 (2)pt naøy coù = - 4 0 2. Töø ñaây ta coù
*Neáu 2 thì pt
x x x x
xx
xx
t t t t a t t t a
x tx t t
t
ñaõ cho coù moät nghieäm
*Neáu 2 thì vôùi moãi giaù trò cuûa cho töông öùng hai giaù trò cuûa x
Neân pt (1) coù ñuùng hai nghieäm phaân bieät pt(1') coù ñuùng hai nghieäm t= 2
hoaëc (1') coù ñuùng
tt
3 2 2
1nghieäm thoûa maõn 2
26
1: Neáu (1') coù ñuùng hai nghieäm t= 2 voâ nghieäm
22 6
2:(1') coù ñuùng moät nghieäm 2
Xeùt haøm soá ( ) 3 9 vôùi 2, ta coù '( ) 3 6 9 3( 1
tt
a
TH a
TH t
f t t t t t f t t t t )( 3)t
Ta có bảng biến thiên:
Dựa vào bảng bt ta thấy pt(1’) có đúng một nghiệm
2t
khi và chỉ khi
2 6 22 4 16aa
f(t)
f’(t)
x
-2
2
1
-3
0
0
+
-
2
22
27

trungtrancbspkt@gmail.com biquyetthanhcong.net
Bài 4:Cho hàm số
( )( )y x x a x b
với a,b là hai số thực dương khác nhau cho
trước.Cmr với mỗi số thực
0;1s
đếu tồn tại duy nhất số thực
1
0: ( ) 2
ss
s
ab
f
( HSG QG bảng A năm 2006)
Giải: Trước hết ta cos BĐT :
()
22
ss s
a b a b
(1) ta có thể cm (1) bằng hàm số hoặc
bằng BĐT Bécnuli
Áp dụng BĐT Côsi và (1) ta có :
1
()
22
ss
s
a b a b
ab
(*) (do
ab
)
Mặt khác ta có:
2 2 ( )( )
'( ) 2 ( )( )
x a b x a x b
fx x a x b
ta dễ dàng cm được f’(x) >0 mọi
x>0 suy ra f(x) đồng biến với x>0 nên
0
( ) ( ) ( ) 2
x
x
ab
Lim f x ab f x Lim f x
(**)
Vì f(x) liên tục khi x>0 nên từ (*) và (**) ta có điều phải cm
Bài tập:
1. Tìm m để pt sau có nghiệm duy nhất thuộc
[0; ]
4
32
(4 6 )sin 3(2 1)sin 2( 2)sin cos (4 3)cos 0m x m x m x x m x
2.Tìm m để số nghiệm của pt:
2 2 4 2
15 2(6 1) 3 2 0x m x m m
không nhiều hơn số
nghiệm của pt:
2 3 6 8
(3 1) 12 2 6 (3 9) 2 0,25
x m m
m x x
(HSG Nghệ an 1998)
3. Tìm tất cả các giá trị a để bpt:
2
ln(1 ) x x ax
nghiệm đúng
0x
4. a)Cmr nếu a >0 là số sao cho bpt:
1
x
ax
đúng với mọi
0x
thì
ae
b) Tìm tất cả các giá trị của a để :
1
x
a x x
(HSG 12 Nam Định 2006)

trungtrancbspkt@gmail.com biquyetthanhcong.net
II.Giải pt bằng phương pháp hàm số:
Định lí 1:Nếu hàm số y=f(x) luôn đb (hoặc luôn ngb) thì số nghiệm của pt : f(x)=k
Không nhiều hơn một và f(x)=f(y) khi và chỉ khi x=y
Định lí 2: Nếu hàm số y=f(x) luôn đb (hoặc luôn ngb) và hàm số y=g(x) luôn ngb (hoặc
luôn đb) trên D thì số nghiệm trên D của pt: f(x)=g(x) không nhiều hơn một
Định lí 3:Cho hàm số y=f(x) có đạo hàm đến cấp n và pt
()
( ) 0
k
fx
có m nghiệm, khi
đó pt
( 1) ( ) 0
k
fx
có nhiều nhất là m+1 nghiệm
Các ví dụ:
Bài 1:Giải pt:
22
3 (2 9 3) (4 2)( 1 1) 0x x x x x
(Olympic 30-4 ĐBSCL 2000)
Giải: Ta thấy pt chỉ có nghiệm trong
1
( ;0)
2
22
22
3 (2 ( 3 ) 3) (2 1)(2 (2 1) 3)
(2 3) (2 3) (1)
pt x x x x
u u v v
Với u=-3x, v=2x+1; u,v>0. Xét hàm số
42
( ) 2 3f t t t t
với t>0
Ta có
3
42
23
'( ) 2 0 0 ( ) ( )
3
tt
f t t f u f v u v
tt
(1)
u=v
-3x=2x+1
1
5
x
là nghiệm duy nhất của pt
Bài 2: Giải pt:
2osx=2 vôùi - ;
22
tg x
e c x
(HSG Lớp 12 Nam Định 2006)
Giải: Xét hàm số :
2
( ) osx vôùi - ;
22
tg x
f x e c x
, ta có
2
2tg 3
23
1 2e os
'( ) 2 . sin sin
cos os
x
tg x cx
f x tgx e x x
x c x
Vì
23
2 2 os 0
tg x
e c x
Nên dấu của f’(x) chính là dấu của sinx. Từ đây ta có
( ) (0) 2f x f
Vậy pt đã cho có nghiệm duy nhất x=0
Bài 3: Giải pt:
2003 2005 4006 2
xx x
(HSG Nghệ an 2005)
Giải: Xét hàm số :
( ) 2003 2005 4006 2
xx
f x x
Ta có:
'( ) 2003 ln2003 2005 ln2005 4006
xx
fx
22
''( ) 2003 ln 2003 2005 ln 2005 0 "( ) 0 voâ nghieäm
f'(x)=0 coù nhieàu nhaát laø moät nghieäm f(x)=0 coù nhieàu nhaát laø hai nghieäm
xx
f x x f x
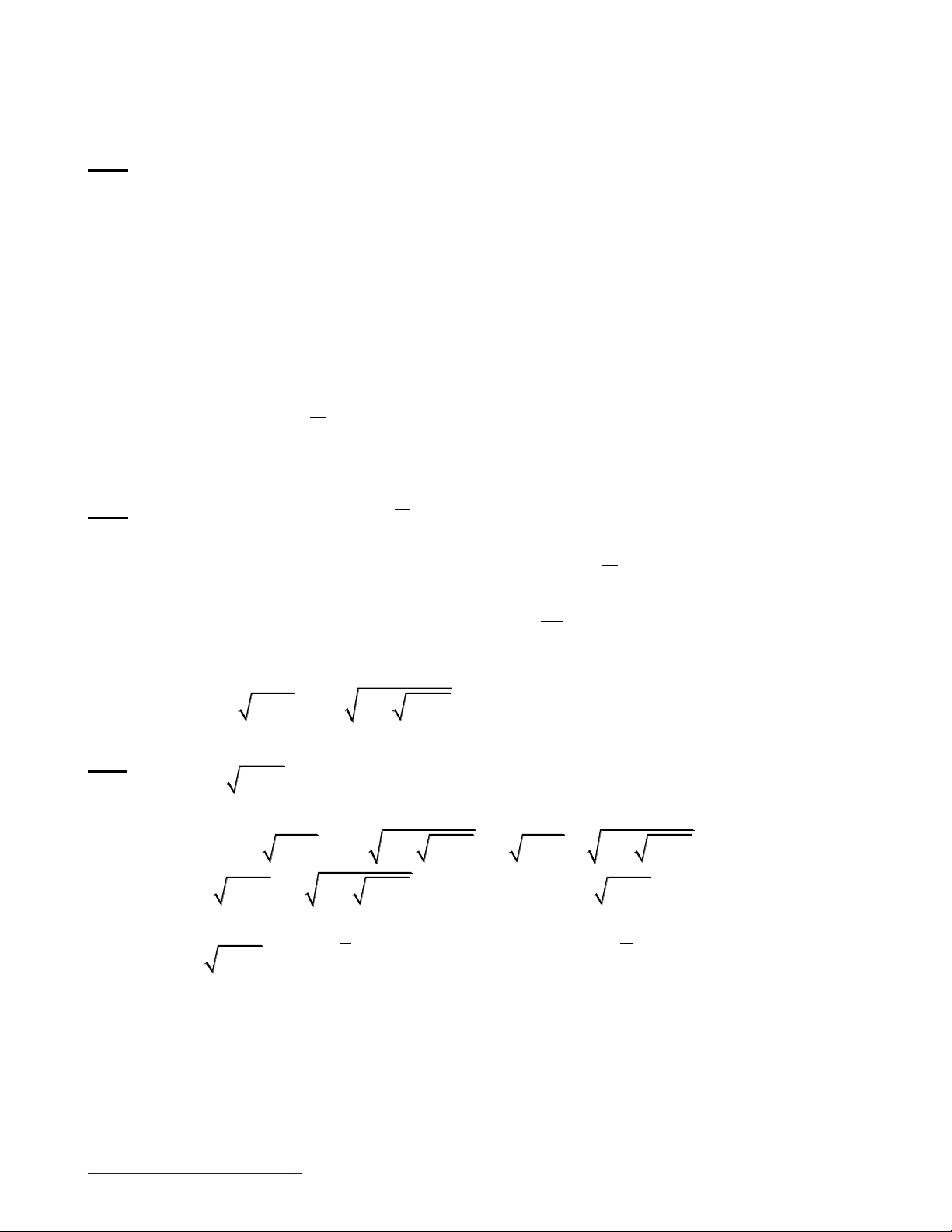
trungtrancbspkt@gmail.com biquyetthanhcong.net
Mà ta thấy f(1)=f(0)=0 nên pt đã cho có hai nghiệm x=0 và x=1
Bài 4: Giải pt:
3
3 1 log (1 2 )
xxx
(TH&TT)
Giải: Đk: x>-1/2
3 3 3
3 1 2 log (1 2 ) 3 log 3 1 2 log (1 2 )
x x x
pt x x x x x
(1)
Xét hàm số:
3
( ) logf t t t
ta có f(t) là hàm đồng biến nên
(1) (3 ) (1 2 ) 3 2 1 3 2 1 0 (2)
x x x
f f x x x
Xét hàm số:
2
( ) 3 2 1 '( ) 3 ln3 2 "( ) 3 ln 3 0
x x x
f x x f x f x
( ) 0fx
có nhiều nhất là hai nghiệm, mà f(0)=f(1)=0 nên pt đã cho có hai nghiệm
x=0 và x=1
Bài 5: Giải hệ pt:
sinx-siny=3x-3y (1)
x+y= (2)
5
, 0 (3)xy
Giải: Từ (2) và (3) ta có :
, (0; )
5
xy
(1) sinx-3x=siny-3y
. Xét hàm số f(t)=sint-3t với
(0; )
5
t
ta có f(t) là hàm nghịch
biến nên f(x)=f(y)
x=y thay vào (2) ta có
10
xy
là nghiệm của hệ
Bài 6: Giải hệ:
(1)
1 1 8 (2)
tgx tgy y x
y x y
(30-4 MOĐBSCL 2005)
Giải: Đk:
1
8
y
xy
(*)
(1)
tgx x tgy y
xy
(do hàm số
( ) f t tgt t
là hàm đồng biến)
Thay vào (2) ta có:
1 1 8 1 8 1y y y y y y
22
1 8 2 8 1 8 4 4 8
88
33
3 8 4 8 8
9 48 64 16 128 9 64 64 0
y y y y y y y y
yy
y y y
y y y y y
Vậy
8 xy
là nghiệm duy nhất của hệ đã cho


























