
Tailieumontoan.com
Điện thoại (Zalo) 039.373.2038
CHUYÊN ĐỀ
CỰC TRỊ HÀM SỐ
Tài liệu sưu tầm, ngày 8 tháng 12 năm 2020
Website: tailieumontoan.com
CHỦ ĐỀ 2. CỰC TRỊ HÀM SỐ
A. KIẾN THỨC CƠ BẢN
1. Định nghĩa: Cho hàm số
()y fx
xác định và liên tục trên khoảng
(;)ab
và điểm
0(;)x ab
.
+ Nếu tồn tại số
0h
sao cho
0
() ( )fx fx
với mọi
00
(; )x x hx h
và
0
xx
thì ta nói hàm số
()fx
đạt cực đại tại
0
x
.
+ Nếu tồn tại số
0h
sao cho
0
() ( )fx fx
với mọi
00
(; )x x hx h
và
0
xx
thì ta nói hàm số
()fx
đạt cực tiểu tại
0
x
.
2. Điều kiện đủ để hàm số có cực trị: Giả sử hàm số
()
y fx
liên tục trên
00
(; )K x hx h
và có đạo
hàm trên
K
hoặc trên
0
\{ }Kx
, với
0h
.
+ Nếu
'( ) 0fx
trên khoảng
00
( ;)x hx
và
'( ) 0fx
trên
00
(; )xx h
thì
0
x
là một điểm cực đại của hàm
số
()fx
.
+ Nếu
'( ) 0fx
trên khoảng
00
( ;)
x hx
và
() 0fx
trên
00
(; )xx h
thì
0
x
là một điểm cực tiểu của
hàm số
()fx
.
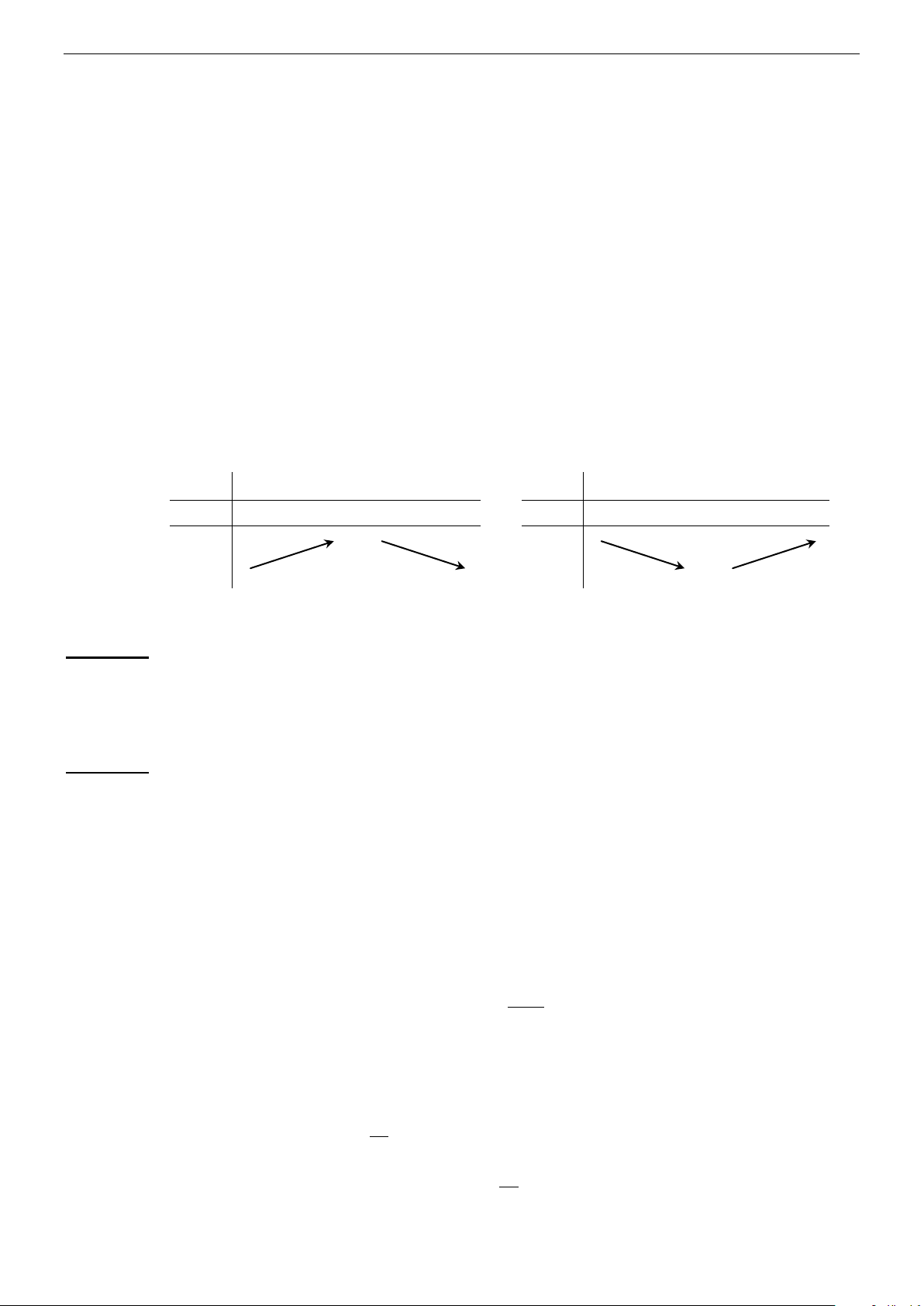
Minh họa bằng bảng biến thiến
B. KỸ NĂNG CƠ BẢN
1. Quy tắc tìm cực trị của hàm số
Quy tắc 1:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính
()fx
. Tìm các điểm tại đó
()fx
bằng 0 hoặc
()fx
không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc 2:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính
()fx
. Giải phương trình
()fx
và ký hiệu
i
x
( 1,2, 3,...)i
là các nghiệm.
Bước 3. Tính
()fx
và
()
i
fx
.
Bước 4. Dựa vào dấu của
()
i
fx
suy ra tính chất cực trị của điểm
i
x
.
2. Kỹ năng giải nhanh các bài toán cực trị hàm số bậc ba
32
y ax bx cx d
(
0a
).
Ta có
2
32y ax bx c
Đồ thị hàm số có 2 điểm cực trị khi phương trình
0y
có hai nghiệm phân biệt
2
30b ac
.
Khi đó đường thẳng qua hai điểm cực trị liên quan tới:
.
18
yy
ya
(CASIO hỗ trợ).
3. Kỹ năng giải nhanh các bài toán cực trị hàm trùng phương.
Cho hàm số:
42
y ax bx c
(
0a
) có đồ thị là
()
C
.
Ta có
3
2
0
4 2; 0
2
x
y ax bx y b
xa
()C
có ba điểm cực trị
0y
có 3 nghiệm phân biệt
0
2
b
a
x
0
xh−
0
x
0
xh+
x
0
xh−
0
x
0
xh+
()fx
′
+
−
()fx
′
−
+
()
fx
CÑ
f
()
fx
CT
f
Liên hệ tài liệu word toán SĐT và zalo: 039.373.2038
Trang 1/38

Website: tailieumontoan.com
Hàm số có 3 cực trị là:
(0; ), ; , ;
24 24
bb
A cB C
aa aa
.
Độ dài các đoạn thẳng:
4
2
,2
22
16
bb b
AB AC BC
aa
a
.
CÔNG THỨC TÍNH NHANH
Ba điểm cực trị tạo thành tam giác
ABC
thỏa mãn dữ kiện
STT
Dữ kiện
Công thức thỏa
0
ab
1
Tam giác
ABC
vuông cân tại
A
3
80ab
2
Tam giác
ABC
đều
3
24 0ab
3 Tam giác
ABC
có góc
BAC
3
8
tan 2
a
b
4 Tam giác
ABC
có diện tích
0ABC
SS
325
0
32 ( ) 0aS b
5 Tam giác
ABC
có diện tích
0
()max S
5
03
32
b
Sa
6 Tam giác
ABC
có bán kính đường tròn nội tiếp
0
ABC
rr
2
03
11
b
r
b
aa
7 Tam giác
ABC
có độ dài cạnh
0
BC m
2
0
. 20am b
8 Tam giác
ABC
có độ dài
0
AB AC n
22 4
0
16 8 0a n b ab
9
Tam giác
ABC
có cực trị
,B C Ox
2
40b ac
10
Tam giác
ABC
có
3
góc nhọn
3
(8 ) 0ba b
11
Tam giác
ABC
có trọng tâm
O
260b ac
12
Tam giác
ABC
có trực tâm
O
3
84 0b a ac
13 Tam giác
ABC
có bán kính đường tròn ngoại tiếp
0ABC
RR
3
8
8
ba
Rab
14
Tam giác
ABC
cùng điểm
O
tạo hình thoi
220b ac
15
Tam giác
ABC
có
O
là tâm đường tròn nội tiếp
3
84 0b a abc
16
Tam giác
ABC
có
O
là tâm đường tròn ngoại tiếp
3
88 0b a abc
17
Tam giác
ABC
có cạnh
..BC k AB k AC
32 2
. 8 ( 4) 0
b k ak
18 Trục hoành chia
ABC
thành hai phần có diện tích bằng nhau
2
42b ac
19
Tam giác
ABC
có điểm cực trị cách đều trục hoành
2
80b ac
20 Phương trình đường tròn ngoại tiếp
ABC
là:
22
22
0
44
x y cy c
ba ba
Liên hệ tài liệu word toán SĐT và zalo: 039.373.2038
Trang 2/38
Website: tailieumontoan.com
BÀI TẬP TRẮC NGHIỆM
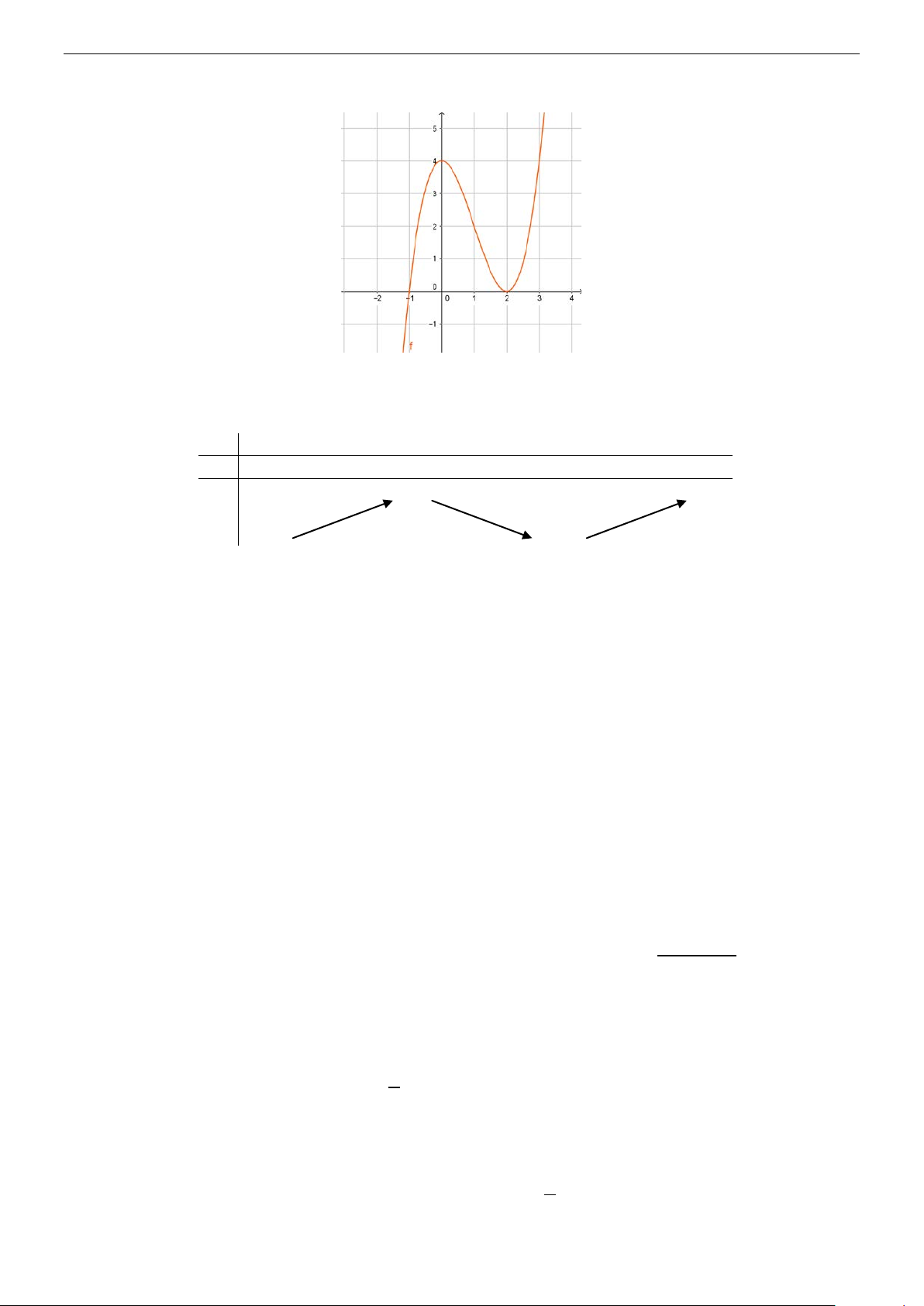
Câu 1. Cho hàm số
()y fx=
có đồ thị như hình vẽ:
Đồ thị hàm số
()y fx
=
có mấy điểm cực trị?
A. 2. B. 1. C. 0. D. 3.
Câu 2. Cho hàm số
()
y fx=
có bảng biến thiên:
Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại
2
x=
. B. Hàm số đạt cực đại tại
3
x=
.
C. Hàm số đạt cực đại tại
4
x=
. D. Hàm số đạt cực đại tại
2x= −
.
Câu 3. Cho hàm số
32
32yx x=−+
. Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực đại tại
2x=
và đạt cực tiểu tại
0
x=
.
B. Hàm số đạt cực tiểu tại
2x=
và đạt cực đại
0
x=
.
C. Hàm số đạt cực đại tại
2x= −
và cực tiểu tại
0
x=
.
D. Hàm số đạt cực đại tại
0
x=
và cực tiểu tại
2
x= −
.
Câu 4. Cho hàm số
42
23yx x=−+
. Khẳng định nào sau đây là đúng?
A. Hàm số có ba điểm cực trị. B. Hàm số chỉ có đúng 2 điểm cực trị.
C. Hàm số không có cực trị. D. Hàm số chỉ có đúng một điểm cực trị.
Câu 5. Biết đồ thị hàm số
331yx x=−+
có hai điểm cực trị
,AB
. Khi đó phương trình đường
thẳng
AB
là:
A.
2.yx= −
B.
2 1.yx= −
C.
2 1.yx=−+
D.
2.yx=−+
Câu 6. Gọi
,Mn
lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số
233
2
xx
yx
++
=+
. Khi đó giá trị
của biểu thức
2
2Mn
−
bằng:
A. 8. B. 7. C. 9. D. 6.
Câu 7. Cho hàm số
32
17 24 8
yx x x=+ −+
. Kết luận nào sau đây là đúng?
A.
1.
CD
x=
B.
2.
3
CD
x=
C.
3.
CD
x= −
D.
12.
CD
x= −
Câu 8. Cho hàm số
42
361yx x=−+
. Kết luận nào sau đây là đúng?
A.
2.
CD
y= −
B.
1.
CD
y=
C.
1.
CD
y= −
D.
2.
CD
y=
Câu 9. Trong các hàm số sau, hàm số nào đạt cực đại tại
3
2
x=
?
x
−∞
2
4
+∞
y
′
+
0
−
0
+
y
−∞
3
2−
+∞
Liên hệ tài liệu word toán SĐT và zalo: 039.373.2038
Trang 3/38

Website: tailieumontoan.com
A.
432
13.
2
y xxx x= −+−
B.
23 2.y xx
=−+ −
C.
2
4 12 8.yxx
= −−
D.
1.
2
x
yx
−
=+
Câu 10. Trong các hàm số sau, hàm số nào chỉ có cực đại mà không có cực tiểu?
A.
42
10 5 7.
y xx
=− −+
B.
32
17 2 5.
y x xx
=− + ++
C.
2.
1
x
yx
−
=+
D.
2
1.
1
xx
yx
++
=−
Câu 11. Cho hàm số
2
3 13 19
3
xx
yx
++
=+
. Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số có
phương trình là:
A.
5 2 13 0.xy− +=
B.
3 13.yx= +
C.
6 13.yx= +
D.
2 4 1 0.
xy+ −=
Câu 12. Cho hàm số
22yxx= −
. Khẳng định nào sau đây là đúng
A. Hàm số có hai điểm cực trị. B. Hàm số đạt cực tiểu tại
0
x=
.
C. Hàm số đạt cực đại
2x=
. D. Hàm số không có cực trị.
Câu 13. Cho hàm số
75
yx x= −
. Khẳng định nào sau đây là đúng
A. Hàm số có đúng 1 điểm cực trị. B. Hàm số có đúng 3 điểm cực trị .
C. Hàm số có đúng hai điểm cực trị. D. Hàm số có đúng 4 điểm cực trị.
Câu 14. Cho hàm số
()y fx
=
có đạo hàm
234
( ) ( 1)( 2) ( 3) ( 5)fx x x x x
′=+− − +
. Hỏi hàm số
()y fx=
có mấy điểm cực trị?
A. 2. B. 3. C.4. D. 5.
Câu 15. Cho hàm số
1
23
( 2)yx x
= −
. Khẳng định nào sau đây là đúng?
A. Hàm số đạt cực tiểu tại
1.x=
B. Hàm số đạt cực đại tại
1x=
.
C. Hàm số không có điểm cực trị. D. Hàm số có đúng 2 điểm cực trị.
Câu 16. Cho hàm số
32
36yxx x=−+ +
. Hàm số đạt cực trị tại hai điểm
12
,xx
. Khi đó giá trị của
biểu thức
22
12
Sx x
= +
bằng:
A.
10
−
. B.
8−
. C.10. D. 8.
Câu 17. Cho hàm số
()y fx=
có đạo hàm trên
. Khẳng định nào sau đây là đúng?
A. Nếu đạo hàm đổi dấu khi
x
chạy qua
0
x
thì hàm số đạt cực tiểu tại
0
x
.
B. Nếu
0
()0fx
′=
thì hàm số đạt cực trị tại
0
x
.
C. Nếu hàm số đạt cực trị tại
0
x
thì đạo hàm đổi dấu khi
x
chạy qua
0
x
.
D. Nếu
00
() ()0fx fx
′ ′′
= =
thì hàm số không đạt cực trị tại
0
x
.
Câu 18. Cho hàm số
()y fx=
. Khẳng định nào sau đây là đúng?
A. Hàm số
()y fx=
đạt cực trị tại
0
x
thì
0
()0fx
′=
.
B. Nếu hàm số đạt cực trị tại
0
x
thì hàm số không có đạo hàm tại
0
x
hoặc
0
()0fx
′=
.
C. Hàm số
()y fx=
đạt cực trị tại
0
x
thì nó không có đạo hàm tại
0
x
.
D. Hàm số
()y fx=
đạt cực trị tại
0
x
thì
0
()0fx
′′ >
hoặc
0
()0fx
′′ <
.
Câu 19. Cho hàm số
()y fx=
xác định trên
,ab[]
và
0
x
thuộc đoạn
,ab[]
. Khẳng định nào sau đây là
khẳng định đúng?
A. Hàm số
()y fx=
đạt cực trị tại
0
x
thì
0
()0fx
′′ <
hoặc
0
()0fx
′′ >
.
B. Hàm số
()y fx=
đạt cực trị tại
0
x
thì
0
()0fx
′=
.
C. Hàm số
()y fx=
đạt cực trị tại
0
x
thì nó không có đạo hàm tại
0
x
.
D. Nếu hàm số đạt cực trị tại
0
x
thì hàm số không có đạo hàm tại
0
x
hoặc
0
()0fx
′=
.
Liên hệ tài liệu word toán SĐT và zalo: 039.373.2038
Trang 4/38


























