
Tailieumontoan.com
Điện thoại (Zalo) 039.373.2038
CHUYÊN ĐỀ
GTLN-GTNN CỦA HÀM SỐ CHỨA
THAM SỐ
Tài liệu sưu tầm, ngày 8 tháng 12 năm 2020

Website: tailieumontoan.com
PHẦN I:
KHÔNG CÓ KIẾN THỨC CẦN NHỚ - KHÔNG BÀI TẬP MẪU.
BÀI TẬP MẪU
(ĐỀ MINH HỌA LẦN 2-BDG 2019-2020) Cho hàm số
( )
1
xm
fx x
+
=+
(
m
là tham số thực). Gọi
S
là
tập hợp tất cả các giá trị của
m
sao cho
[ ]
( )
[ ]
( )
0;1
0;1
max min 2fx fx+=
. Số phần tử của
S
là
A.
6
. B.
2
. C.
1
. D.
4
.
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán GTLN – GTNN của hàm số liên tục trên một đoạn (cố gắng đưa ra
phương pháp chung cho dạng toán này nếu được)
…………………………………………………………………………………………………….
2. KIẾN THỨC CẦN NHỚ: (thầy cô liệt kê hết các công thức cần dùng cho biến đổi của bài toán)
+ Quy tắc xác định GTLN – GTNN của hàm số liên tục trên một đoạn:
Xét hàm số
( )
y fx=
liên tục trên đoạn
[ ]
;ab
.
B1: Tính đạo hàm
( )
fx
′
. Tìm các điểm
12
, ,...,
n
xx x
trên khoảng
( )
;ab
tại đó
( )
fx
′
bằng 0 hoặc
( )
fx
′
không xác định.
B2: Tính
( ) ( ) ( ) ( ) ( )
12
, , ,..., ,
n
fa fx fx fx fb
.
B2: Tìm số lớn nhất
M
và số nhỏ nhất
m
trong các số trên.
Ta có:
[ ]
( )
[ ]
( )
;
;
max ; min
ab
ab
M fx m fx= =
.
…………………………………………………………………………………………………….
3. HƯỚNG GIẢI: (nếu là câu hỏi lý thuyết hay câu hỏi dễ quá chỉ có 1; 2 dòng thì bỏ qua bước này)
B1: Xét trường hợp
1m=
⇒
thấy thỏa mãn bài toán.
B2: Tính đạo hàm
( )
fx
′
. Xét các trường hợp
( ) ( )
0, 0fx fx
′′
><
để suy ra
[ ]
( )
0;1
max fx
và
[ ]
( )
0;1
min fx
.
B3: Biện luận để suy ra
[ ]
( )
0;1
max fx
và
[ ]
( )
0;1
min fx
từ đó tìm ra đáp số của bài toán.
Từ đó, ta có thể giải bài toán cụ thể như sau:
Lời giải
Chọn B
+ Với
1m=
: ta có
( )
[ ]
1, 0; 1fx x= ∀∈
.
DẠNG TOÁN 48: GTNN – GTNN (TÌM GTLN – GTNN CỦA HÀM PHỤ THUỘC THAM
SỐ TRÊN ĐOẠN .
Liên hệ tài liệu word toán sđt và zalo: 039.373.2038 Trang1
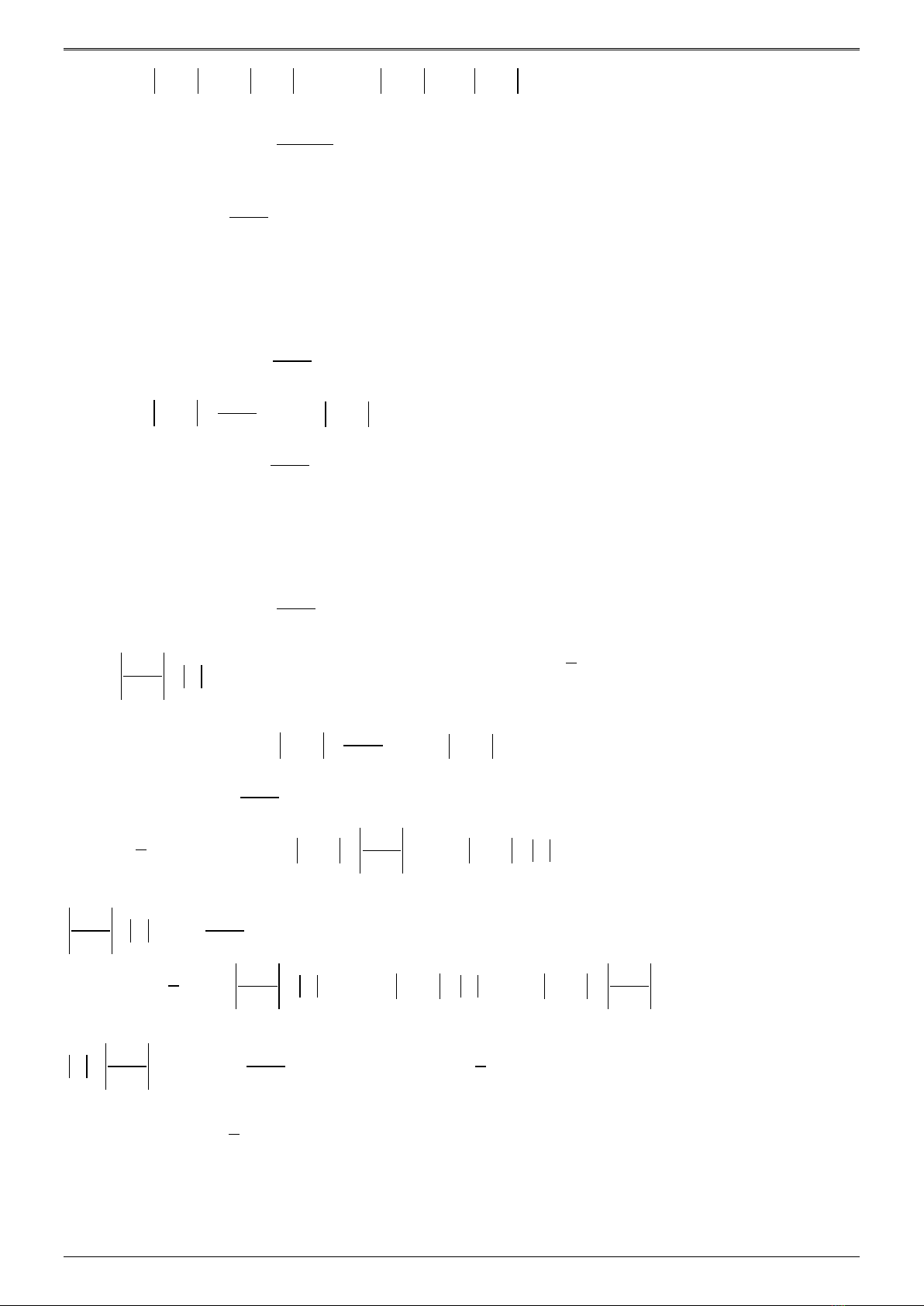
Website: tailieumontoan.com
Do đó
[ ]
( )
[ ]
( )
[ ]
( )
[ ]
( )
0;1 0;1
0;1 0;1
max min 1 max min 2fx fx fx fx==⇒+=
(thỏa mãn đề bài).
+ Với
1m≠
, ta có:
( ) ( )
[ ]
2
10, 0; 1
1
m
fx x
x
−
′= ≠ ∀∈
+
.
Có
( ) ( )
1
0 ;1 2
m
f mf +
= =
.
- Nếu
10 1mm− <⇔ >
thì
( )
0fx
′<⇒
Hàm số
( )
fx
nghịch biến trên các khoảng
( )
;1−∞ −
và
( )
1;− +∞
.
Khi đó:
[ ]
( ) ( )
0;1
1
min10
2
m
fx f +
= = >
và
[ ]
( ) ( )
0;1
max 0 0fx f m= = >
.
Suy ra
[ ]
( )
0;1
1
min 2
m
fx +
=
và
[ ]
( )
0;1
max fx m=
.
Theo bài ra ta phải có:
123 3 1
2
m
m mm
+
+ =⇔ =⇔=
(loại).
- Nếu
10 1mm− >⇔ <
thì
( )
0fx
′>⇒
Hàm số
( )
fx
đồng biến trên các khoảng
( )
;1−∞ −
và
( )
1;− +∞
.
Khi đó:
[ ]
( ) ( )
0;1
1
max 1 2
m
fx f +
= =
và
[ ]
( ) ( )
0;1
min 0fx f m= =
.
Ta xét
( )
222
1
11 4 3 2 10 3
21
m
mm m m mm
m
<−
+
<⇔+< ⇔ −−>⇔
>
.
+) Khi
01m≤<
, ta có
[ ]
( )
0;1
1
max 2
m
fx +
=
và
[ ]
( )
0;1
min fx m=
.
Theo bài ra ta phải có:
123 3 1
2
mm mm
++=⇔ =⇔=
(loại).
+) Khi
10
3m−≤ <
, ta có
[ ]
( )
0;1
1
max 2
m
fx +
=
và
[ ]
( )
0;1
min fx m=
.
Theo bài ra ta phải có:
11
2 2 33
22
mm
m mmm
++
+ = ⇔ − = ⇔− =− ⇔ =
(loại).
+) Khi
1
3
m<−
, ta có
1
2
mm
+<
nên
[ ]
( )
0;1
max fx m=
và
[ ]
( )
0;1
1
min 2
m
fx +
=
.
Theo bài ra ta phải có:
11 5
2 2 35
22 3
mm
m m mm
++
+ = ⇔− − = ⇔− = ⇔ =−
(thỏa mãn).
Vậy, ta có tập
5;1
3
S
= −
, do đó số phần tử của tập
S
bằng 2.
Liên hệ tài liệu word toán sđt và zalo: 039.373.2038 Trang2

Website: tailieumontoan.com
Bài tập tương tự và phát triển :
Câu 1. Cho hàm số
26y x xm=−+
(
m
là tham số thực) thỏa mãn
[ ]
0;4
min 1y= −
. Mệnh đề nào sau đây
đúng?
A.
10m<−
. B.
10 7m− < ≤−
. C.
70m−< <
. D.
0 10m<<
.
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
( )
y fx=
trên
đoạn
[ ]
;ab
.
Phương pháp
- B1: Tính đạo hàm
()fx
′
.
- B2: Tìm tất cả các nghiệm
[;]
i
x ab∈
của phương trình
() 0fx
′=
và tất cả các điểm
[;]
iab
α
∈
làm cho
()fx
′
không xác định.
- B3: Tính
()fa
,
()fb
,
()
i
fx
,
()
i
f
α
.
- B4: So sánh các giá trị tính được và kết luận
[ ]
;
max ( )
ab
M fx=
,
[ ]
;
min ( )
ab
m fx=
.
………………………………………………………………………………………………….
2. KIẾN THỨC CẦN NHỚ ( nhắc lại các công thức, định lý cần dùng cho phần lời giải chi tiết)
( )
1nn
x nx
−
′=
.
( ) ( )
1,
22
u
xu
xu
′
′′
= =
.
( )
2
ax b ad bc
cx d cx d
′
+−
=
+
+
.
( )
..uv u v v u
′′′
= +
.
2
..u uv vu
vv
′′′
−
=
.
( ) ( )
..ku ku k
′′
= ∈
.
…………………………………………………………………………………………………….
3. HƯỚNG GIẢI:
B1: Tính đạo hàm
()fx
′
.
B2: Tìm tất cả các nghiệm
[;]
i
x ab∈
của phương trình
() 0fx
′=
và tất cả các điểm
[;]
i
ab
α
∈
làm cho
()fx
′
không xác định.
B3: Tính
()fa
,
()fb
,
()
i
fx
,
()
i
f
α
.
B4: So sánh các giá trị tính được và kết luận
[ ]
;
max ( )
ab
M fx=
,
[ ]
;
min ( )
ab
m fx=
.
Liên hệ tài liệu word toán sđt và zalo: 039.373.2038 Trang3

Website: tailieumontoan.com
Từ đó ta có thể giải bài toán cụ thể như sau:
Lời giải
Chọn D
Ta có
2 40 3yx x
′= −=⇔=
.
Suy ra
[ ]
( ) ( ) ( )
{ }
{ }
0;4
min min 0 ; 3 ; 4 min ; 9; 8 9y y y y mm m m= = − −=−
.
Theo giả thiết ta có
91 8mm− =−⇔ =
.
Vậy
0 10m<<
.
Câu 2. Cho hàm số
2
6y x xm=−+
(
m
là tham số thực) thỏa mãn
[ ] [ ]
0;4 0;4
min 2 max 18yy−=−
. Mệnh đề
nào sau đây đúng?
A.
10m<−
. B.
10 7m− < ≤−
. C.
70m−< <
. D.
0 10m<<
.
Lời giải
Chọn D
Ta có
2 40 3yx x
′= −=⇔=
.
Suy ra
+)
[ ]
( ) ( ) ( )
{ }
{ }
0;4
min min 0 ; 3 ; 4 min ; 9; 8 9y y y y mm m m= = − −=−
+)
[ ]
( ) ( ) ( )
{ }
{ }
0;4
max max 0 ; 3 ; 4 max ; 9; 8y y y y mm m m= = − −=
.
Theo giả thiết ta có
[ ] [ ]
0;4 0;4
min 2 max 23 9 2 18 9y y mm m− =− ⇒ −− =− ⇔ =
.
Vậy
0 10m<<
.
Câu 3. Cho hàm số
2
6y x xm=−+
(
m
là tham số thực) thỏa mãn
[ ]
0;4
max 3y=
. Mệnh đề nào sau đây
đúng?
A.
10m<−
. B.
10 7m− < ≤−
. C.
70m−< <
. D.
0 10m<<
.
Lời giải
Chọn D
Ta có
2 40 3yx x
′= −=⇔=
.
Suy ra
[ ]
( ) ( ) ( )
{ }
{ }
0;4
max max 0 ; 3 ; 4 max ; 9; 8y y y y mm m m= = − −=
.
Theo giả thiết ta có
[ ]
0;4
max 3 3ym=⇒=
.
Vậy
0 10m<<
.
Câu 4. Cho hàm số
26y x xm=−+
(
m
là tham số thực) thỏa mãn
[ ] [ ]
0;4 0;4
min max 23yy+=−
. Mệnh đề nào
sau đây đúng?
A.
10m<−
. B.
10 7m− < ≤−
. C.
70m−< <
. D.
0 10m<<
.
Lời giải
Liên hệ tài liệu word toán sđt và zalo: 039.373.2038 Trang4


























