
CHUYEÂN ÑEÀ 3:
DOØNG ÑIEÄN XOAY CHIEÀU vaø DAO ÑOÄNG ÑIEÄN TÖØ
HÖÔÙNG DAÃN GIẢI
CAÂU 1: Khi Δt raát nhoû, caùc giaù trò töùc thôøi cuûa ñieän xoay chieàu coù theå xem nhö doøng ñieän
khoâng ñoåi.
Choïn C
CAÂU 2:
R
)ZZ(
R
U
)ZZ(R
U
R
Z
U
RRIP 2
CL
2
AB
2
CL
2
2
AB
AB
2
AB
2
AB −
+
=
−+
===
UAB khoâng ñoåi, PABmax khi maãu soá min. Heä quaû BÑT Cauchy cho ta
2
LC
(Z Z )
R* R
−=(ZL-ZC)2= haèng soá
Neân maãu soá min khi: R
)ZZ(
R
2
CL −
=.
Choïn D
CAÂU 3: Ta coù: 2
CL
2
2
AB
AB )ZZ(R
U
RP −+
=
Vôùi L, C; UAB vaø PAB xaùc ñònh ta bieán ñoåi ñöôïc
aR2 + bR + c=0 (hoaëc veõ ñoà thò) seõ tìm ñöôïc hai giaù trò cuûa R thoaû PAB<Pmax
Choïn B
CAÂU 4 : 2
CL
2
ABL
LL )ZZ(R
U.Z
I.ZU −+
==
Duøng moät trong 3 caùch
• Ñaïo haøm : ULmax ⇔ 0
dZ
dU
L
L=
• Ñöa ZL xuoáng maãu soá vaø bieán ñoåi maãu soá veà daïng parobol
• Veõ giaûn ñoà Fresnel vaø aùp duïng ñònh lyù haøm sin.
Ta ñöôïc: ULmax khi
C
2
C
2
LZ
ZR
Z+
=
Choïn C
CAÂU 5 : PAB=R.I2
Do R xaùc ñònh neân PABmax khi Imax
Maïch coäng höôûng.
Choïn A
CAÂU 6 : Nhö CAÂU 5 Pmax khi R
U
Imax =

Luùc ñoù: UL=ZL.Imax=R
U.ZL vaø UC=ZC.Imax=R
U.ZL
Choïn D
CAÂU 7 : Maïch coäng höôûng, lyù luaän nhö CAÂU 6: loaïi B vaø D
Maët khaùc: ZAB=R neân UAB=UR ⇒ loaïi C
Do ZL=ZC ⇒ Lω=ω.C
1 hay L= 2
.C
1
ω
Choïn A
CAÂU 8 :
f thay ñoåi, PAB=R.I2 cöïc ñaïi khi Imax
Luùc ñoù Pmax=UAB.I vì cosϕ = 1.
Choïn D
CAÂU 9
Haøm ñieàu hoaø coù daïng sin hoaëc cosin theo t.
Choïn C
CAÂU 10 :
Taùc duïng nhieät khoâng phuï thuoäc chieàu doøng ñieän.
Choïn A
CAÂU 11
ϕAB= (uAB; i) coù
tgϕAB=R
ZZ CL − phuï thuoäc ñaëc tính maïch ñieän
• ϕAB>0: maïch coù tính caûm khaùng, uAB nhanh hôn i
⇒ loaïi B
• ϕAB<0: maïch coù tính dung khaùng, i nhanh hôn uAB
⇒ loaïi C
Choïn D
CAÂU 12
t
0=0 luùc α=0)B,N( =
r
r
thì ϕ=0
neân Φ = BScosωt
Choïn C
CAÂU 13
Maùy phaùt ñieän khoâng theå thay ñoåi dieän tích khung daây.
Choïn D
CAÂU 14
p= n
f60 nhöng soá caëp cöïc laø haèng soá khoâng phuï thuoäc vaøo f vaø n
Choïn B
CAÂU 15
Xem Saùch Giaùo khoa 12, trang 48
Choïn C
CAÂU 16

cosϕAB=
AB
Z
R laø haøm soá chaün neân khoâng theå bieát ϕAB döông hay aâm
Choïn C
CAÂU 17
Cuoän caûm luoân luoân coù ñieän trôû thuaàn khaùc 0
Choïn C
CAÂU 18
cosϕAB=1
Maïch coäng höôûng Z=R hay U=UR
Choïn D
CAÂU 19: tgϕLC=±∞=
−
0
ZZ CL hay ϕLC=2
π
±
Choïn C
CAÂU 20: i nhanh pha hôn uC ⇒ loaïi A vaø C
Choïn B
CAÂU 21
sinϕAB=tgϕAB×cosϕAB=
AB
CL
AB
CL
Z
ZZ
Z
R
R
ZZ
−
=×
− Choïn D
CAÂU 22: i chaäm pha hôn uL moät goùc 2
π
⇒ loaïi A
vaø B
Maët khaùc cosωt=sin(ωt+ 2
π)
⇒ loaïi D
Choïn C
CAÂU 23: tgϕAB=R
ZZ CL − chæ duøng ñeå tính tröïc tieáp ñoä leäch pha uAB ñoái vôùi i maø khoâng
tính tröïc tieáp goùc leäch pha giöõa 2 hieäu ñieän theá.
Choïn A
CAÂU 24: 1
2
π
ϕ= −ϕ
1
neân tg = tg
1
ϕ2
2
1
2t
π
⎛⎞
−ϕ =
⎜⎟
g
ϕ
⎝⎠
Hay L2
1L
ZR
RZ
=
Do ñoù ZL2 = R1R2 Vaäy 12
R.R
L2f
=π
Choïn B
CAÂU 25: Khi R noái tieáp C thì maïch coù tính dung khaùng, i luoân luoân sôùm pha hôn u.
Choïn D
CAÂU 26: Coäng höôûng khi ω
=ω C
1
L hay 2
L
1
Cω
=
Choïn B
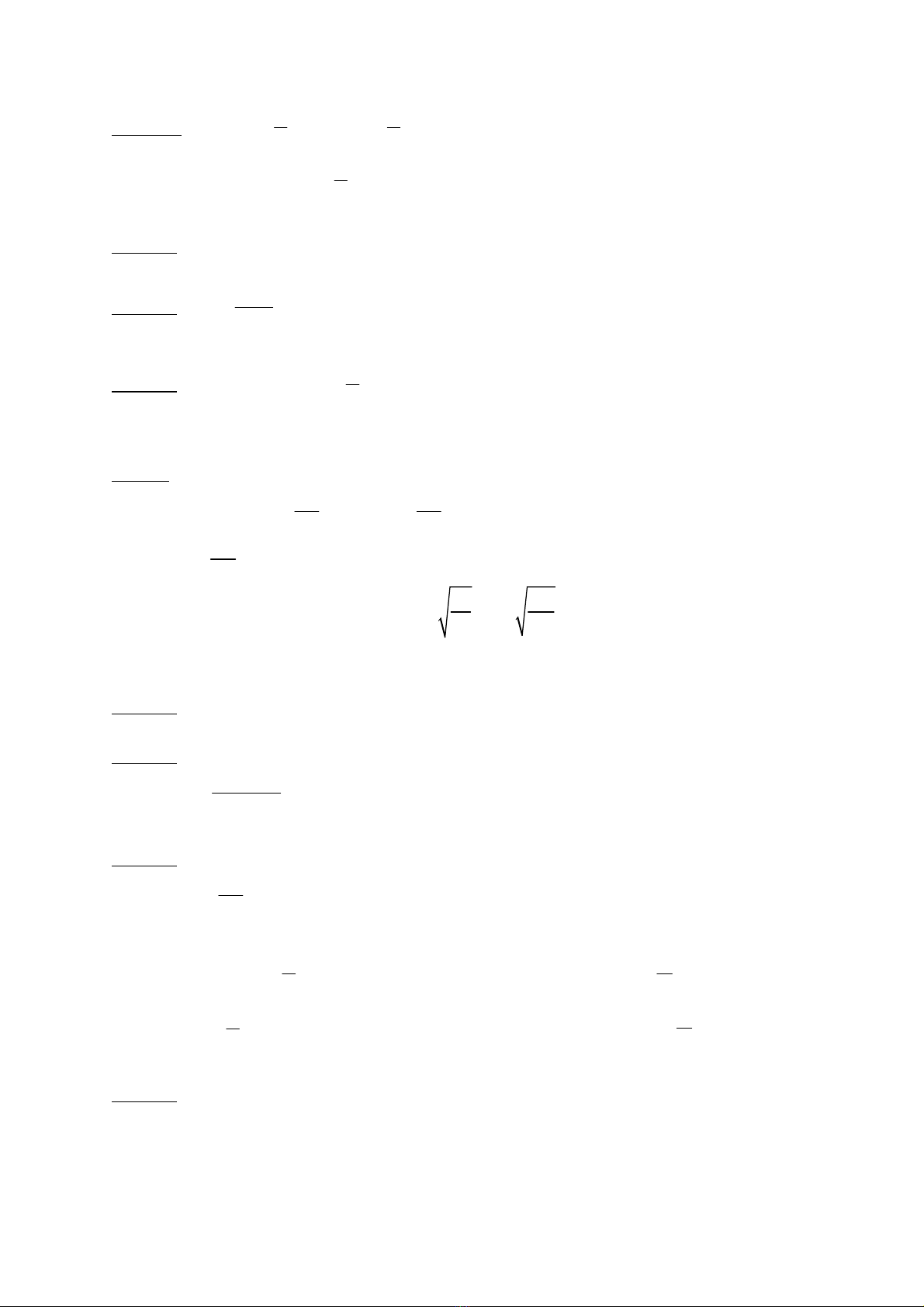
CAÂU 27: i=I0sin(ωt- 6
π
)= I0cos(ωt+ 3
π
)
ϕAB=pha uAB-pha iAB=- 3
π
Choïn C
CAÂU 28: Khi coäng höôûng UL=UC≠0
Choïn C
CAÂU 29: ω
=C
1
ZC ⇒ khi C taêng thì ZC giaûm.
Choïn D
CAÂU 30: cosϕAB=0 ⇒ ϕAB=2
π
±
Maïch chæ coù L vaø C nhöng I khaù lôùn (xem Saùch Giaùo khoa 12, trang 61)
Choïn B
Caâu 31 : Goïi P laø coâng suaát taûi ñieän taïi Baø Ròa,
Δ
P laø coâng suaát hao phí ta coù:
Tæ leä hao phí laø P
nP
Δ
= maø
2
2
P
PR
U
Δ= (xem SGK lôùp 12 trang 77)
Neân: 2
RP
nU
= Vôùi R laø ñieän trôû toång coäng caùc daây taûi (laø ñaïi löôïng khoâng ñoåi)
Do ñoù: RP = n1U12 = n2U22 1
21
2
n10
U U 200 400KV
n2,5
→= = =
U 200KVΔ=
Choïn B
CAÂU 32 : Phaàn öùng taïo ra doøng ñieän.
Choïn C
CAÂU 33 : uR ñoàng pha vôùi i neân ñoä leäch pha giöõa uR vaø uAB vaãn tính baèng coâng thöùc
tgϕAB=R
ZZ CL −
Choïn C
CAÂU 34 : q=Q0sin(ωt+ϕ)
neân )tcos(I)tcos(Q
dt
dq
i00 ϕ+ω=ϕ+ωω== , vôùi I0=ωQ0
luùc t0=0 thì i=0 hay q0=±Q0
sau 4
1 chu kyø thì q1=0 neân Δq=q0-q1=Q0=ω
0
I
trong
2
1 chu kyø thì ñieän löôïng qua tieát dieän laø 2Δq=2 ω
0
I
Choïn C
CAÂU 38 : Hieäu ñieän theá giöõa 2 daây pha hoaëc 1 daây pha vaø 1 daây trung hoøa coù giaù trò hieäu
duïng laø Ud hoaëc UP neân khoâng theå bieán thieân .
Loaïi A vaø C
Do caùch maéc tam giaùc khoâng coù daây trung hoøa neân caàn coù caùc taûi ñoái xöùng toát hôn hình
sao. Loaïi B.
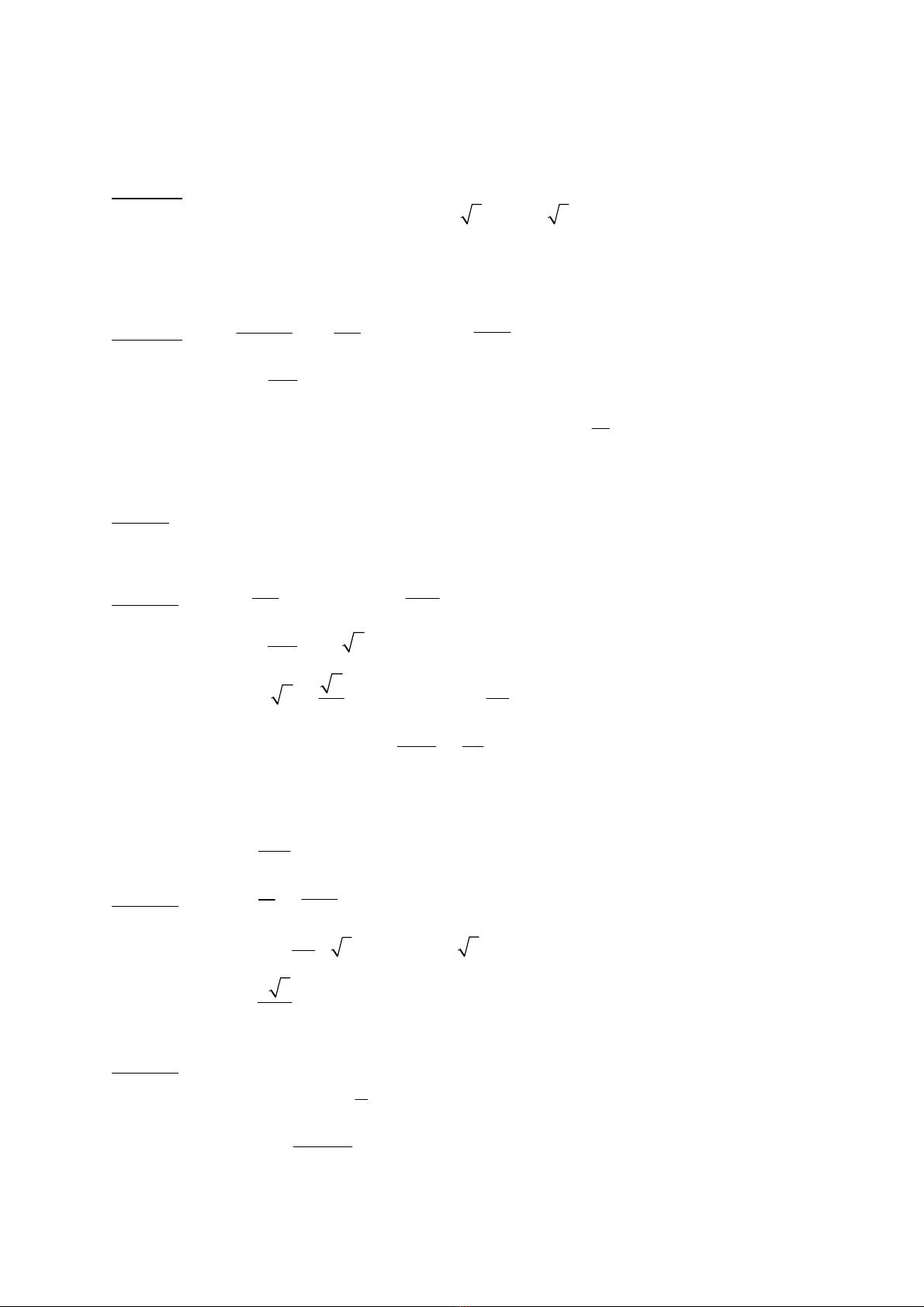
Khi coù cheânh leäch giöõa caùc taûi tieâu thuï thì doøng ñieän qua daây trung hoøa yeáu hôn haún doøng
ñieän trong caùc daây pha: chæ caàn daây coù tieát dieän nhoû.
Choïn D
CAÂU 61
Khi maùy phaùt ñieän maéc hình sao thì Ud = P
3U 220 3 380V==
Muoán ñoäng cô hoaït ñoäng bình thöôøng thì caàn cung caáp hieäu ñieän theá hai ñaàu moãi pha
cuûa noù laø 380(V) = Ud neân caàn maéc ñoäng cô hình tam giaùc.
Choïn A
CAÂU 64 : PP P
H1
PP
−Δ Δ
==−
Vôùi
2
2
RP
PU
Δ=
Suy ra: H = 2
RP
1U
− Hay RP = (1 – H).U2
Vôùi R vaø P coá ñònh, giaûm hieäu ñieän theá 2 laàn ta ñöôïc U’ = U
2
Neân RP = (1 – H)U2 = (1 – H’)U’2 Hay H’ = 1 – 4(1 – H)
Choïn C
Caâu 73 : Thoâng tin trong vuõ truï duøng soùng cöïc ngaén vì noù khoâng bò haáp thuï bôûi taàng ñieän
ly
Choïn B
Caâu 115: I = R
U
R = 0,5A ; ZAB = AB
U
I = 160
Ω
Z
rL = rL
U
I = 60 2Ω ; r = ZrLcos rL
ϕ
r = 60
2 x 2
2 = 60
Ω
; tg rL
ϕ
= L
Z
r = 1
Neân: ZL = r = 60 L = Ω→60
100
π
= 3
5
π
(H) loaïi B
Maët khaùc: = (R + r)2 + (ZL – ZC)2
2
AB
Z
1602 = (100 + 60)2 + (ZL – ZC)2 → ZC = ZL = 60
Ω
Vaäy: C =
3
10
6
−
π
(F) Choïn A
Caâu 118: R = 2
P
I = 18
0, 09 = 200
Ω
Loaïi C
tg =
RL
ϕL
Z3
R= → ZL = 200 3
Vaäy L = 23
π Choïn B
Caâu 120: R = 100 ; ZL = 200Ω
Ω
(uAB ; i) =
AB
ϕ4
π
− (Vì i nhanh hôn uAB)
tg =
AB
ϕLC
ZZ
R
− = 1 ZC = ZL + R = 300
→
Ω


























