
CÁC CHUYÊN ĐỀ LUYỆN THI ĐẠI HỌC 2009 - PHẦN SỐ PHỨC
http://violet.vn/kinhhoa Ngọc Vinh
1
sè phøc
PHẦN I. CÁC DẠNG TOÁN
VẤN ĐỀ 1
d¹ng ®¹i sè cña sè phøc
Céng, trõ, nh©n, chia sè phøc
A. TÓM TẮT KIẾN THỨC
1. Sè phøc
Mét biÓu thøc d¹ng z = a + bi, trong ®ã a vµ b lµ nh÷ng sè thùc vµ i tháa m·n i
2
= -1 ®îc gäi
lµ mét sè phøc.
a ®îc gäi lµ phÇn thùc, b ®îc gäi lµ phÇn ¶o, i ®îc gäi lµ ®¬n vÞ ¶o.
TËp c¸c sè phøc ®îc kÝ hiÖu lµ .
Sè phøc cã phÇn ¶o b»ng 0 gäi lµ sè thùc nªn R
.
Sè phøc cã phÇn thùc b»ng 0 gäi lµ sè ¶o. 0 = 0 + 0i lµ sè võa thùc võa ¶o.
2. Hai sè phøc b»ng nhau
'
z a+bi (a,b ), z' a'+b' i (a',b' ); z z' '
a a
b b
3. Céng, trõ hai sè phøc
z a+bi (a,b ), z' a'+b' i (a',b' )
z + z' (a + a' ) + (b + b') i, z z' (a - a') + (b - b' )i
Sè ®èi cña sè phøc z = a + bi lµ sè phøc ; - z = - a – bi.
4. Nh©n hai sè phøc
z a+bi (a,b ), z' a'+b' i (a',b' ); zz' ' ' ( ' ' )aa bb ab a b i
5. M«®un cña sè phøc, sè phøc liªn hîp
z = a +bi (a, b
) th× m«®un cña z lµ
2 2
z = a +b
z = a +bi (a, b
) th× sè phøc liªn hîp cña z lµ
z
= a - bi.
Ta cã:
2
2 2
zz' = z z' , zz a b z , z + z' = z + z', zz'=z z', z = z
* z lµ sè thùc khi vµ chØ khi z =
z
6. Chia cho sè phøc kh¸c 0
NÕu z = a + bi (a, b
) kh¸c kh«ng th× sè phøc nghÞch ®¶o cña z lµ
1
-1
z = z
2
z
.
Th¬ng cña z' cho z kh¸c kh«ng lµ:
z' z'z
-1
z'z
zzz
. Ta cã:
'
' ' '
,
z
z z z
z z z z
.
7. BiÓu diÔn h×nh häc cña sè phøc
Sè phøc z = a + bi (a, b
) ®îc biÓu diÔn bëi M(a; b) trong mÆt ph¼ng to¹ ®é Oxy hay
cßn gäi lµ mÆt ph¼ng phøc.
Trôc Ox biÓu diÔn c¸c sè thùc gäi lµ trôc thùc, trôc Oy biÓu diÔn c¸c sè ¶o gäi lµ trôc ¶o
Sè phøc z = a + bi (a, b
) còng ®îc biÓu diÔn bëi vect¬
( ; )u a b
, do ®ã M(a; b) lµ ®iÓm
biÓu diÔn cña sè phøc z = a + bi (a, b
) còng cã nghÜa lµ
OM
biÓu diÔn sè phøc ®ã.
Ta cã:NÕu
,u v
theo thø tù biÓu diÔn c¸c sè phøc z, z' th×
CÁC CHUYÊN ĐỀ LUYỆN THI ĐẠI HỌC 2009 - PHẦN SỐ PHỨC
http://violet.vn/kinhhoa Ngọc Vinh
2
u v
biÓu diÔn sè phøc z + z',
u v
biÓu diÔn sè phøc z – z-1, k
( )u k
biÓu diÔn sè phøc
kz,
OM u z
, víi M lµ ®iÓm biÓu diÔn cña z.
B. C¸c d¹ng bµi tËp
I. X¸c ®Þnh tæng, hiÖu, tÝch, th¬ng cña c¸c sè phøc
1) Ph¬ng ph¸p gi¶i
Áp dông c¸c quy t¾c céng, trõ, nh©n, chia hai sè phøc, chó ý c¸c tÝnh chÊt giao ho¸n, kÕt hîp
®èi víi c¸c phÐp to¸n céng vµ nh©n.
2) C¸c vÝ dô
VÝ dô 1: T×m ph©n thùc, phÇn ¶o cña c¸c sè phøc sau
a) i + (2 - 4i) - (3 - 2i); b)
3 3
( 1 ) (2 )i i
Bµi gi¶i
a) Ta cã: i + (2 - 4i) - (3 - 2i) = ((0 + 2) + (1 - 4)i) + (- 3 + 2i) = (2 - 3) + (-3 + 2)i = -1 - i.
VËy sè phøc ®· cho cã phÇn thùc lµ - 1, phÇn ¶o lµ - 1.
b) Sö dông c¸c quy t¾c céng, trõ, nh©n hai sè phøc ta cã
3 3 2 2 3 3 3 3
( 1 ) ( 1) 3( 1) 3( 1) 2 2 , ( 2 ) ( 2) ( ) 8i i i i i i i i
Do ®ã nhËn ®îc kÕt qu¶ cña bµi to¸n lµ 2 + 10i
VÝ dô 2: TÝnh
1
1 3
2 2 i
Bµi gi¶i
Ta cã :
1 3 1 3
1 3
2 2 2 2
1 2 2
1 3 1 3
2 2 2 2
i i
i
i i
VÝ dô 3: TÝnh
2 3 2009
1 ...i i i i
Bµi gi¶i
Ta cã:
2010 2 3 2009
1 (1 )(1 ... )i i i i i i
. Mµ
2010
1 2i
. Nªn
2
2 3 2009
1 ... 1
i i i i i
,
2 3 2009
1 ... 1i i i i i
.
VÝ dô 4: TÝnh
100
(1 )i
Bµi gi¶i
NhËn thÊy
2
(1 ) (1 )(1 ) 2i i i i
.
Suy ra
100 2 50 50 50 50 50
(1 ) ((1 ) ) ( 2 ) ( 2) ( ) 2i i i i
.
VÝ dô 5: Cho sè phøc
1 3
2 2
z i
.
H·y chøng minh r»ng:
;
1
2 2 3
1 0; 1.z z z z z
z
.
Bµi gi¶i
Do
1 3
22 2
z i
. Nªn
1 3 1 3
21 ( ) ( ) 1 0
2 2 2 2
z z i i
;

CÁC CHUYÊN ĐỀ LUYỆN THI ĐẠI HỌC 2009 - PHẦN SỐ PHỨC
http://violet.vn/kinhhoa Ngọc Vinh
3
L¹i cã
1 3
1 1 1 3
2 2
1 2 2
1 3
2 2
i
i
zi
. Suy ra
1
2
z z z
.
H¬n n÷a ta cã
31
z
.
VÝ dô 6: T×m sè phøc z, nÕu
20zz
.
Bµi gi¶i
§Æt z = x + yi, khi ®ã
2 2 2 2 2 2 2 2
2
2 2 2 2
2
0 ( ) 0 2 0
00
0 (1 ) 0
0
0
0
2 0
(1 ) 0
0
00,
0
1
0 (do 1 0)
0
z x yi x y x y x y xyi
xx
y y y y
x y x y
y
y
xy
x x
x x
x
x y
y
y
x x
y
z
0
0, 1
0, 1
0, 0
x y
x y
y x
VËy cã ba sè phøc tho¶ m·n ®iÒu kiÖn lµ z = 0; z = i; z = - i.
II. BiÓu diÔn sè phøc trong mÆt ph¼ng to¹ ®é
1) Ph¬ng ph¸p gi¶i
§Ó biÓu diÔn mét sè phøc cÇn dùa vµo ®Þnh nghÜa vµ c¸c tÝnh chÊt sau:
NÕu sè phøc z ®îc biÓu diÔn bëi vect¬
u
, sè phøc z' ®îc biÓu diÔn bëi vect¬
'u
, th×
z + z' ®îc biÓu diÔn bëi
'u u
; z - z' ®îc biÓu diÔn bëi
'u u
; - z ®îc biÓu diÔn bëi
u
.
2) C¸c vÝ dô.
VÝ dô 1: Gi¶ sö M(z) lµ ®iÓm trªn mÆt ph¼ng to¹ ®« biÓu diÔn sè phøc z. T×m tËp hîp nh÷ng
®iÓm M(z) tháa m·n ®iÒu kiÖn sau
a)
1 2z i
; b)
2z i z
.
Bµi gi¶i
a) §Æt z = x + yi suy ra z - 1 + i = (x - 1) + (y + 1)i. Nªn hÖ thøc
1 2z i
trë thµnh
2 2 2 2
( 1) ( 1) 2 ( 1) ( 1) 4.x y x y
VËy tËp hîp c¸c ®iÓm M(z) trªn mÆt ph¼ng to¹ ®é biÓu diÔn c¸c sè phøc z tháa m·n gi¶ thiÕt
lµ ®êng trßn t©m I(1; - 1) b¸n kÝnh R = 2.
b) Gäi A (- 2 ; 0), B(0 ; 1). Khi ®ã
2z i z
( 2)z z i
hay lµ
M(z)A = M(z)B. VËy tËp hîp c¸c ®iÓm M(z) lµ ®êng trung trùc cña ®o¹n th¼ng AB.
NhËn xÐt: Víi phÇn b ta cã thÓ thøc hiÖn c¸ch gi¶i nh ®· lµm ë phÇn a. Tuy nhiªn ®Ó
thÓ thùc hiÖn c¸ch gi¶i nh vËy lµ ta ®· dùa v¸o nhËn xÐt sau:
NÕu vÐct¬
u
cña mÆt ph¼ng phøc biÓu diÔn sè phøc z th× ®é dµi cña vect¬
u
lµ
u z
, vµ tõ
®ã nÕu c¸c ®iÓm A, B theo thø tù biÓu diÔn c¸c sè phøc z, z' th×
'AB z z
.

CÁC CHUYÊN ĐỀ LUYỆN THI ĐẠI HỌC 2009 - PHẦN SỐ PHỨC
http://violet.vn/kinhhoa Ngọc Vinh
4
VÝ dô 2: Trong c¸c sè phøc z tho¶ m·n ®iÒu kiÖn
3
2 3 2
z i
. T×m sè phøc z cã modul nhá
nhÊt.
Bµi gi¶i
XÐt biÓu thøc
3
2 3 2
z i
(1). §Æt z = x + yi. Khi ®ã (1) trë thµnh
3 9
2 2
( 2) ( 3) ( 2) ( 3) .
2 4
x y i x y
Do ®ã c¸c ®iÓm M biÓu diÔn sè phøc z tho¶ m·n (1) n»m trªn ®êng trßn ( ) t©m
I(2; -3) vµ b¸n kÝnh R =
3
2
.
Ta cã
z
®¹t gi¸ trÞ nhá nhÊt khi vµ chØ khi
®iÓm M n»m trªn ®êng trßn ( ) vµ gÇn O nhÊt. Do ®ã M lµ giao ®iÓm cña ( ) vµ ®êng th¼ng
OI, víi M lµ giao ®iÓm gÇn O h¬n.
Ta cã OI =
4 9 13
. KÎ MH
Ox. Theo ®Þnh lÝ talet cã
3
13 9 6 13 9
213 3 13
3 2 2
13
MH OM MH
OI
6 13 9 78 9 13
26
2 13
MH
.
L¹i cã
3
13 2 13 3 26 3 13
2
2 13
13 13
OH OH
.
VËy sè phøc cÇn t×m lµ :
26 3 13 78 9 13
13 26
z i
.
VÝ dô 3: Chøng minh r»ng víi mäi sè phøc z, w, ta cã
z w z w
. §¼ng thøc x¶y ra khi
nµo?
Bµi gi¶i
Gäi A, B, C lÇn lît lµ c¸c ®iÓm biÓu diÔn cña c¸c sè phøc z, w, z + w.
Ta cã
, ,z OA w OB z w OC
. Tõ OC
OA + AC suy ra
z w z w
.
H¬n n÷a OC = OA + AC khi vµ chØ khi O, A, C th¼ng hµng vµ A thuéc ®o¹n th¼ng OC.
Khi O
A (hay z
0) ®iÒu ®ã cã nghÜa lµ cã sè k
0 ®Ó
AC kOA
tøc lµ w = kz. (Cßn khi z
= 0, râ rµng
z w z w
).
VËy
z w z w
khi vµ chØ khi z = 0 hoÆc nÕu z
0 th× tån t¹i
k R
®Ó w = kz.
c. bµi tËp
1. Chøng minh r»ng víi mäi sè phøc z, w ta ®Òu cã
z w z w
. DÊu b»ng x¶y ra khi nµo?
2. Trong mÆt ph¼ng phøc, bèn ®iÓm ph©n biÖt A, B, C, D theo thø tù biÓu diÔn c¸c sè phøc z, w,
u, v tho¶ m·n c¸c tÝnh chÊt:
O
H
2
M
I
- 3
x
y
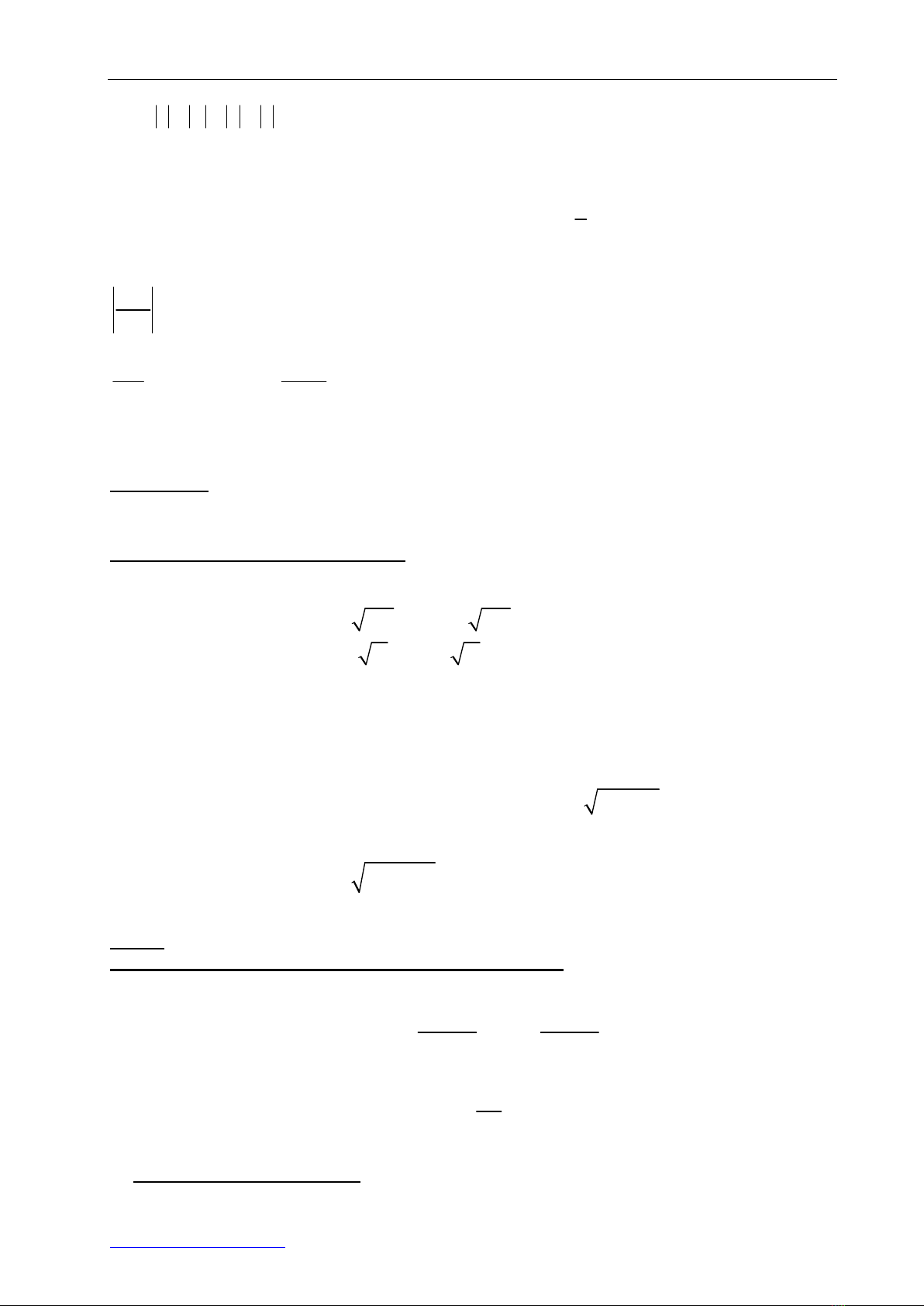
CÁC CHUYÊN ĐỀ LUYỆN THI ĐẠI HỌC 2009 - PHẦN SỐ PHỨC
http://violet.vn/kinhhoa Ngọc Vinh
5
a)
1z w u v
;
b) z + w + u + v = 0.
3. Cho sè phøc z = m + (m - 3)i, m
R
a) T×m m ®Ó biÓu diÔn cña sè phøc n»m trªn ®êng ph©n gi¸c thø hai y = - x;
b) T×m m ®Ó biÓu diÔn cña sè phøc n»m trªn hypebol
2
yx
;
c) T×m m ®Ó kho¶ng c¸ch cña ®iÓm biÓu diÔn sè phøc ®Õn gèc to¹ ®é lµ nhá nhÊt.
4. X¸c ®Þnh tËp hîp c¸c ®iÓm trong mÆt ph¼ng phøc biÓu diÔn c¸c sè phøc tho¶ m·n hÖ thøc
3
z
z i
.
5. XÐt c¸c ®iÓm A, B, C trong mÆt ph¼ng phøc theo thø tù biÓu diÔn c¸c sè phøc
4 2 6
; (1 )(1 2 );
1 3
i i
i i
i i
.
a) Chøng minh ABC lµ tam gi¸c vu«ng c©n;
b) T×m sè phøc biÓu diÔn bëi ®iÓm D sao cho tø gi¸c ABCD lµ h×nh vu«ng.
VẤN ĐỀ 2
C¨n bËc hai cña sè phøc vµ ph¬ng tr×nh bËc hai
A. KiÕn thøc cÇn nhí
I. §Þnh nghÜa c¨n bËc hai cña sè phøc
Cho sè phøc w mçi sè phøc z tho¶ m·n z2 = w ®îc gäi lµ mét c¨n bËc hai cña sè phøc w.
a) NÕu w lµ sè thùc
+ w < 0 th× cã hai c¨n bËc hai:
&wi wi
+ w
0 th× cã hai c¨n bËc hai:
&w w
.
b) NÕu w lµ sè phøc khi ®ã ta thùc hiÖn c¸c bíc:
+ Gi¶ sö w= a + ib, ®Æt z = x + iy lµ mét c¨n bËc hai cña w tøc lµ:
2
z w
khi ®ã ta cã
hÖ:
2 2 (1)
2 (2)
x y a
xy b
B×nh ph¬ng 2 vÕ cña (1) vµ (2) råi céng l¹i ta ®îc
2 2 2 2
x y a b
Do vËy ta ®îc hÖ:
2 2
2 2 2 2
(1)
(2')
x y a
x y a b
Gi¶i hÖ t×m ®îc
2
x
vµ
2
y
suy ra x vµ y ®Ó t×m z.
Chó ý: Theo (2) ta cã nÕu b > 0 th× x, y cïng dÊu. NÕu b < 0 th× x, y tr¸i dÊu.
II. C«ng thøc nghiÖm cña ph¬ng tr×nh bËc hai hÖ sè phøc
Cho PT:
20; (1) ( , , , 0)ax bx c a b c a
vµ cã
24b ac
+ NÕu
0
pt cã hai nghiÖm lµ
1 2
;
2 2
b b
x x
a a
Trong ®ã
lµ mét c¨n bËc hai cña
.
+ NÕu
= 0 th× pt cã nghiÖm kÐp:
1 2 2
b
x x a
.
B. C¸c d¹ng bµi tËp
I. Gi¶i ph¬ng tr×nh bËc nhÊt
1) Ph¬ng ph¸p gi¶i


























