https://www.nbv.edu.vn/ 1
VẤN ĐỀ 1. HÀM SỐ LƯỢNG GIÁC & PHƯƠNG TRÌNH LƯỢNG GIÁC
1. Hàm số lượng giác
a) Hàm số
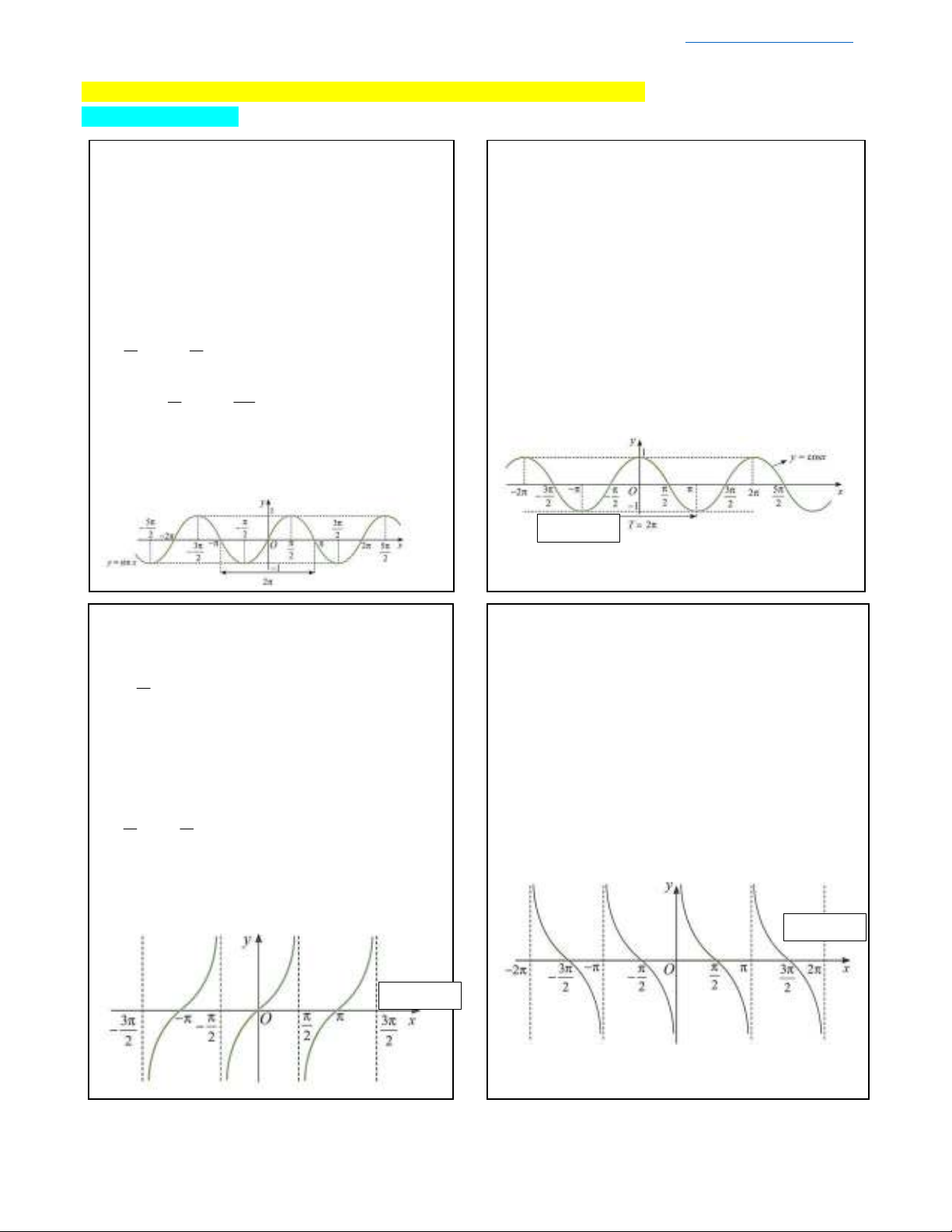
siny x
- Hàm số
siny x
có tập xác định
và có tập
giá trị là
[ 1;1]
.
- Hàm số
sin
là hàm số lẻ và tuần hoàn với chu
kì
2
.
- Hàm số
sin
đồng biến trên mỗi khoảng
2 ; 2
2 2
k k
và nghịch biến trên mỗi
khoảng
3
2 ; 2
2 2
k k
với
k
.
- Đồ thị hàm số
sin
nhận gốc toạ độ làm tâm
đối xứng.
b) Hàm số
cosy x
- Hàm số
cosy x
có tập xác định
và có tập
giá trị là
[ 1;1]
.
- Hàm số côsin là hàm số chẵn và tuần hoàn với
chu kì
2
.
- Hàm số côsin đồng biến trên mỗi khoảng
( 2 ; 2 )k k
và nghịch biến trên mỗi khoảng
( 2 ; 2 )k k
với
k
.
- Đồ thị hàm số côsin nhận trục
Oy
làm trục đối
xứng.
c) Hàm số
tany x
- Hàm số
tany x
có tập xác định
\ |
2k k
và có tập giá trị là
.
- Hàm số tang là hàm số lẻ và tuần hoàn với chu
kì
.
- Hàm số tang đồng biến trên mỗi khoảng
;
2 2
k k
với
k
.
- Đồ thị hàm số tang nhận gốc toạ độ làm tâm
đối xứng.
d) Hàm số
coty x
- Hàm số
coty x
có tập xác định
\{ | }k k
và có tập giá trị
.
- Hàm số côtang là hàm số lẻ và tuần hoàn với chu
kì
.
- Hàm số côtang nghịch biến trên các khoảng
( ; )k k
với
k
.
- Đồ thị hàm số côtang nhận gốc toạ độ làm tâm
đối xứng.
nbv.edu.vn
nbv.edu.vn
nbv.edu.vn

https://www.nbv.edu.vn/ 2
2. Phương trình lượng giác
a) Phương trình
sin
x m
- Nếu
| | 1
m
thì phương trình vô nghiệm.
- Nếu
| | 1
m
thì tồn tại duy nhất số thực
;
2 2
thoả mãn
sin
m
.
Khi đó sin
x m
2
sin sin ( )
2
x k
x k
x k .
Chú ý
- Khi
{ 1;0;1}
m
công thức nghiệm trên được
viết gọn lại là:
-
sin 0
x x k
.
-
sin 1 2
2
x x k
.
-
sin 1 2
2
x x k
.
- Nếu góc
được cho bằng đơn vị độ thì công
thức nghiệm trên trở thành:
360
sin sin ( )
180 360
x k
x k
x k
- Nếu
( )u x
và
( )v x
là hai biểu thức của biến
x
thì
sin ( ) sin ( )u x v x
( ) ( ) 2
( )
( ) ( ) 2
u x v x k k
u x v x k
b) Phương trình
cos x m
- Nếu
| | 1
m
thì phương trình
cos x m
vô
nghiệm.
- Nếu
| | 1
m
thì tồn tại duy nhất
[0; ]
thoả
mãn
cos m
.
Khi đó
cos x m
2
cos cos ( )
2
x k
x k
x k .
Chú ý
- Khi
{ 1;0;1}
m
công thức nghiệm trên được
viết gọn lại là:
-
cos 0
2
x x k
.
-
cos 1 2x x k
.
-
cos 1 2x x k
.
- Nếu góc
được cho bằng đơn vị độ thì công
thức nghiệm trên trở thành:
360
cos cos ( )
360
x k
x k
x k
- Nếu
( )u x
và
( )v x
là hai biểu thức của biến
x
thì
cos ( ) cos ( )u x v x
( ) ( ) 2 ( )
u x v x k k
c) Phương trình
tan x m
- Phương trình
tan x m
có nghiệm với mọi
m
.
- Tồn tại duy nhất
;
2 2
thoả mãn
tan m
.
Khi đó
tan x m
tan tan ( )
x x k k
.
Chú ý. Nếu góc
được cho bằng đơn vị độ thì
công thức nghiệm trên trở thành:
tan tan 180 ( )
x x k k
d) Phương trình
cot x m
- Phương trình
cot x m
có nghiệm với mọi
m
.
- Tồn tại duy nhất
;
2 2
thoả mãn
cot m
.
Khi đó
cot x m
cot cot ( )
x x k k
.
Chú ý. Nếu góc
được cho bằng đơn vị độ thì
công thức nghiệm trên trở thành:
cot cot 180 ( )
x x k k
https://www.nbv.edu.vn/ 3
VẤN ĐỀ 2. DÃY SỐ - CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN
1. Dãy số
a) Định nghĩa.
Một hàm số
u
xác định trên tập hợp các số nguyên dương
*
được gọi là một dãy số vô hạn (hay gọi tắt là dãy
số). Kí hiệu dãy số là
( )u n
.
Dạng khai triển của dãy số
( )u n
là
1 2
, , , ,
n
u u u
, trong đó
( )
n
u u n
được gọi là số hạng thứ
n
(hay còn gọi
là số hạng tổng quát) của dãy số.
b) Dãy số tăng, dãy số giảm
- Dãy số
n
u
được gọi là dãy số tăng nếu
*
1
,
n n
n u u
.
- Dãy số
n
u
được gọi là dãy số giảm nếu
*
1
,
n n
n u u
.
2. Cấp số cộng
a) Định nghĩa.
Cấp số cộng là một dãy số (vô hạn hay hữu hạn) mà
trong đó, kể từ số hạng thứ hai, mỗi số hạng đều bằng
tổng của số hạng đứng ngay trước nó với một số
d
không đổi, nghĩa là:
n
u
là cấp số cộng
1
, 2
n n
u u d n
.
Số
d
được gọi là công sai của cấp số cộng.
b) Tính chất
- Nếu
n
u
là một cấp số cộng thì kể từ số hạng thứ
hai, mỗi số hạng (trừ số hạng cuối đối với cấp số cộng
hữu hạn) đều là trung bình cộng của hai số hạng đứng
kề nó trong dãy, tức là:
1 1
, 2
2
k k
k
u u
u k
.
- Ba số
, ,a b c
(theo thứ tự đó) lập thành một cấp số
cộng nếu
2a c b
.
- Nếu một cấp số cộng có số hạng đầu tiên
1
u
và công
sai
d
thì số hạng tổng quát
n
u
của nó được xác định
bởi công thức:
1
( 1)
n
u u n d
.
- Giả sử
n
u
là một cấp số cộng có công sai
d
. Gọi
1 2
n k n
S u u u u
Khi đó:
1 1
2 ( 1)
2 2
n
n
n u u n u n d
S
.
nbv.edu.vn
3. Cấp số nhân
a) Định nghĩa.
Cấp số nhân là một dãy số (hữu hạn hay vô hạn) mà
trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng
tích của số hạng đứng ngay trước nó và một số
q
không đổi, nghĩa là:
n
u
là cấp số nhân
1
, 2
n n
u u q n
.
Số
q
được gọi là công bội của cấp số nhân.
b) Tính chất
- Nếu
n
u
là một cấp số nhân thì kể từ số hạng thứ
hai, bình phương của mỗi số hạng (trừ số hạng cuối
đối với cấp số nhân hữu hạn) bằng tích của hai số
hạng đứng kề nó trong dãy, tức là:
2
1 1
, 2
k k k
u u u k
.
- Nếu
, ,a b c
là ba số khác 0, thì ba số
, ,a b c
theo thứ
tự đó lập thành một cấp số nhân khi và chỉ khi
2
b ac
.
- Nếu một cấp số nhân có số hạng đầu trên
1
u
và công
bội
0
q
thì số hạng tổng quát
n
u
của nó được xác
định bởi công thức:
1
1
, 2
n
n
u u q n
.
- Giả sử
n
u
là một cấp số nhân có công bội
q
. Gọi
1 2
1
n
n k n
k
S u u u u
. Khi đó:
Nếu
1
q
thì
1
n
S nu
. Nếu
1
q
thì
1
1
.
1
n
n
q
S u
q

https://www.nbv.edu.vn/ 4
VẤN ĐỀ 3. GIỚI HẠN DÃY SỐ, GIỚI HẠN HÀM SỐ
1. Giới hạn dãy số
2. Giới hạn của hàm số
Một số quy tắc tính giới hạn hàm số
a) Một số giới hạn thường dùng
-
*
1
lim 0, ;
k
n
k
n
-
lim 0, | | 1;
n
n
q q
- Nếu
, 1
n n
u v n
và
lim 0
n
n
v
thì
lim 0
n
n
u
.
Ta nói dãy số
n
u
có giới hạn là số thực
a
khi
n
dần tới dương vô cực nếu
lim 0
n
n
u a
, kí hiệu
lim
n
n
u a
hay
n
u a
khi
n
.
b) Giới hạn vô cực của dãy số
-
lim
k
n
n
, với
k
là số nguyên dương;
-
lim
n
n
q
, với
1
q
.
c) Một số quy tắc tính giới hạn dãy số
- Nếu
lim
n
n
u a
và
lim
n
n
v b
thì:
-
lim ;
n n
n
u v a b
-
lim
n n
n
u v a b
;
-
lim . ;
n n
n
u v a b
-
lim ( 0)
n
nn
uab
v b
.
- Nếu
0
n
u
với mọi
n
và
lim
n
n
u a
thì
0
a
và
lim
n
n
u a
.
nbv.edu.vn
d) Cấp số nhân lùi vô hạn
Cấp số nhân vô hạn
n
u
có công bội
q
với
| | 1
q
được gọi là cấp số nhân lùi vô hạn. Tổng vô hạn của
các số hạng trong cấp số nhân lùi vô hạn được tính
bởi công thức:
1
1 2
(| | 1)
1
n
u
S u u u q
q
- Nếu
lim
n
n
u a
và
lim
n
n
v
(hoặc
lim
n
n
v
) thì
lim 0
n
nn
u
v
.
- Nếu
lim 0, lim 0
n n
n n
u a v
và
0
n
v
với mọi
n
thì
lim
n
nn
u
v
.
- Nếu
lim
n
n
u
và
lim 0
n
n
v a
thì
lim
n n
n
u v
.
a) Giả sử
0
lim ( )
x x
f x L
và
0
lim ( ) ,( , )
x x
g x M L M
. Khi đó:
-
0
lim[ ( ) ( )]
x x
f x g x L M
;
-
0
lim[ ( ) ( )]
x x
f x g x L M
;
-
0
lim[ ( ) ( )]
x x
f x g x L M
.
Đặc biệt, nếu
c
là một hằng số thì
0
lim[ ( )]
x x
c f x cL
;
- Nếu
0
M
thì
0
( )
lim ( )
x x
f x L
g x M
.
Chú ý. Những quy tắc trên vẫn đúng khi thay
0
x x
bởi
x
hoặc
x
.
nbv.edu.vn
b) Với mọi số nguyên duơng
,k n
, ta có:
-
lim
k
x
x
;
-
1
lim 0;
k
x
x
- , 2
lim
, 2 1;
k
x
k n
xk n
-
1
lim 0
k
x
x
.

https://www.nbv.edu.vn/ 5
3. Hàm số liên tục
a) Định nghĩa.
Cho hàm số
( )y f x
xác định trên
( ; )a b
chứa điểm
0
x
. Hàm số
( )f x
được gọi là liên tục tại điểm
0
x
nếu
0
0
lim ( )
x x
f x f x
.
- Hàm số
( )y f x
được gọi là liên tục trên
( ; )a b
nếu nó liên tục tại mọi điểm thuộc khoảng này.
- Hàm số
( )y f x
được gọi là liên tục trên
[ ; ]a b
nếu nó liên tục trên
( ; )a b
và
lim ( ) ( ), lim ( ) ( )
x a x b
f x f a f x f b
.
Về tính liên tục của các hàm số sợ cấp cơ bản đã biết, ta có:
- Hàm số đa thức và các hàm số
sin , cosy x y x
liên tục trên
.
- Các hàm số
tan , cot ,
y x y x y x
và hàm phân thức hữu tỉ (thương của hai đa thức) liên tục trên tập xác
định của chúng.
b) Một số tính chất cơ bản
Giả sử hai hàm số
( )y f x
và
( )y g x
liên tục tại điểm
0
x
. Khi đó:
- Các hàm số
( ) ( ), ( ) ( )y f x g x y f x g x
và
( ) ( )y f x g x
liên tục tại
0
x
;
- Hàm số
( )
( )
f x
y
g x
liên tục tại
0
x
nếu
0
0
g x
.
VẤN ĐỀ 4. HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
1. Luỹ thừa với số mũ thực
Luỹ thừa với số mũ thực (của một số thực dương) có các tính chất như luỹ thừa với số mũ nguyên. Cụ thể với
, , 0, 0
a b a b
và
,x y
ta có
; ; ; ( ) ;
x
x x
y
x y x y x y x xy x x x
y x
a a a
a a a a a a a b ab
a b b
2. Lôgarit
a) Khái niệm lôgarit
Cho
a
là một số thực dương khác 1 và
M
là một số thực dương. Số thực
thoả mãn
a M
gọi là lôgarit cơ
số
a
của
M
, kí hiệu là
log
a
M
. Như vậy
log
a
M a M
.
Chú ý. Không có lôgarit của số âm và lôgarit của số 0. Cơ số của lôgarit phải là số dương và khác 1.
b) Tính chất của lôgarit
- Với
0 1, 0
a M
và
là số thực tuỳ ý, ta có
log
log 1 0; log 1; ; log
a
M
a a a
a a M a
- Quy tắc tính lôgarit: Cho
0 1
a
và
, 0
M N
đồng thời
là số thực tuỳ ý, ta có
c) Giả sử
0
lim ( )
x x
f x L
. Khi đó:
-
0
lim | ( ) | | |;
x x
f x L
-
0
lim ( )
a
a
x x
f x L
với
a
là số lẻ.
- Nếu
( ) 0
f x
với mọi
0
\
x J x
, trong đó
J
là một khoảng nào đó chứa
0
x
, thì
0
L
và
0
lim ( )
a
a
x x
f x L
với
a
là số chẵn.
nbv.edu.vn

















