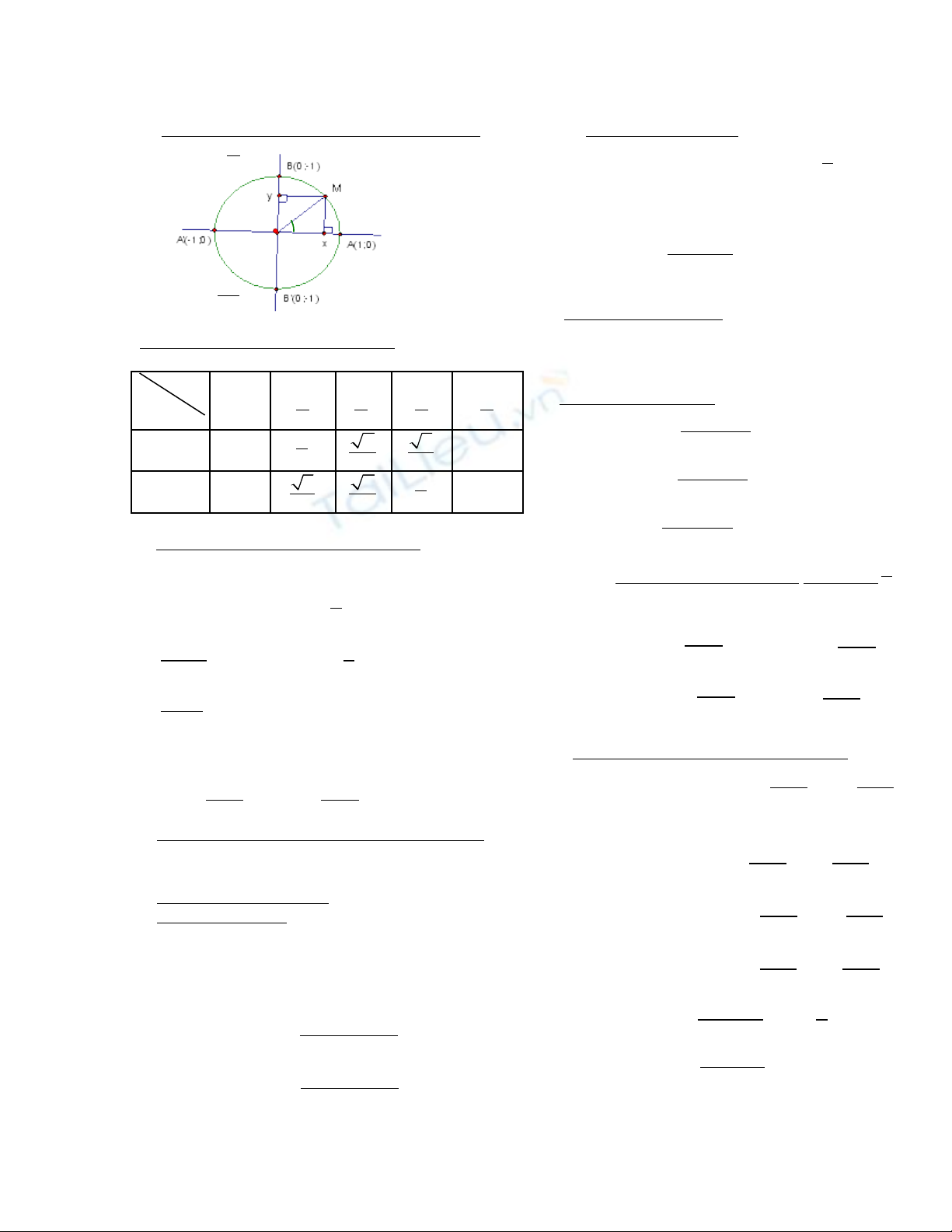
CÔNG TH C L NG GIÁCỨ ƯỢ
A/ Đ ng tròn l ng giác, giá tr l ng giác:ườ ượ ị ượ
B ng giá tr c a các góc đ c bi t:ả ị ủ ặ ệ
Góc
GTLG
00
(0)
300
(
6
π
)
450 (
4
π
)
600
(
3
π
)
900
(
2
π
)
Sin 0
1
2
2
2
3
2
1
Cos 1
3
2
2
2
1
2
0
B/ Các h th c L ng Giác C B n:ệ ứ ượ ơ ả
( )
( )
+ α + α = ∀α∈
π
+ α α = ∀α ≠ ∈
π
+ = + α ∀α ≠ + π ∈
α
+ = + α ∀α ≠ π ∈
α
2 2
2
2
2
2
sin cos 1 R
tan .cot 1 k ,k Z
2
11 tan k ,k Z
cos 2
11 cotg k ,k Z
sin
H qu : ệ ả
• sin2x = 1-cos2x ; cos2x = 1- sin2x
• tanx=
1
cot x
;
1
cot tan
xx
=
C/ Giá Tr Các Cung Góc Liên Quan Đ c Bi tị ặ ệ :
“ Cos đ i, Sin bù, Ph chéo, tan cot l ch ố ụ ệ π”
D/. Công th c l ng giácứ ượ
1. Công th c c ng:ứ ộ
cos (a – b) = cosa.cosb + sina.sinb
cos (a + b) = cosa.cosb – sina.sinb
sin (a – b) = sina.cosb – cosa.sinb
sin (a + b) = sina.cosb + cosa.sinb
tan(a – b) =
tan tan
1 tan .tan
−
+
a b
a b
tan(a + b) =
tan tan
1 tan .tan
+
−
a b
a b
2. Công th c nhân đôi:ứ
sin2a = 2sina.cosa ⇒
1
sina.cosa= sin2
2a
cos2a = cos2a – sin2a = 2cos2a – 1 = 1 – 2 sin2a
tan2a =
3. Công th c nhân baứ:
sin3a = 3sina – 4sin3a
cos3a = 4cos3a – 3cosa
4.Công th c h b c:ứ ạ ậ
cos2a =
1 cos 2
2
a+
sin2a =
1 cos 2
2
a−
tg2a =
1 cos 2
1 cos 2
a
a
−
+
5. Công th c tính sinx, cosx,tanxứ theo t=tan
2
x
:
sinx =
2
2
1
t
t+
cosx =
2
2
1
1
t
t
−
+
tanx =
2
2
1
t
t−
cotx =
2
1
2
t
t
−
6. Công th c bi n đ i t ng thành tích ứ ế ổ ổ
a b a b
cosa cosb 2cos cos
2 2
+ −
+ =
a b a b
cosa cosb 2sin sin
2 2
+ −
− = −
a b a b
sina sinb 2sin cos
2 2
+ −
+ =
a b a b
sina sinb 2cos sin
2 2
+ −
− =
sin( )
tan tan ( , , )
cos .cos 2
±
± = ≠ + ∈
a b
a b a b k k Z
a b
ππ
sin( )
cot cot ( , , )
sin .sin
+
+ = ≠ ∈
a b
a b a b k k Z
a b
π
1
sinα
2
π
0
π
3
2
π
cosα
0
α
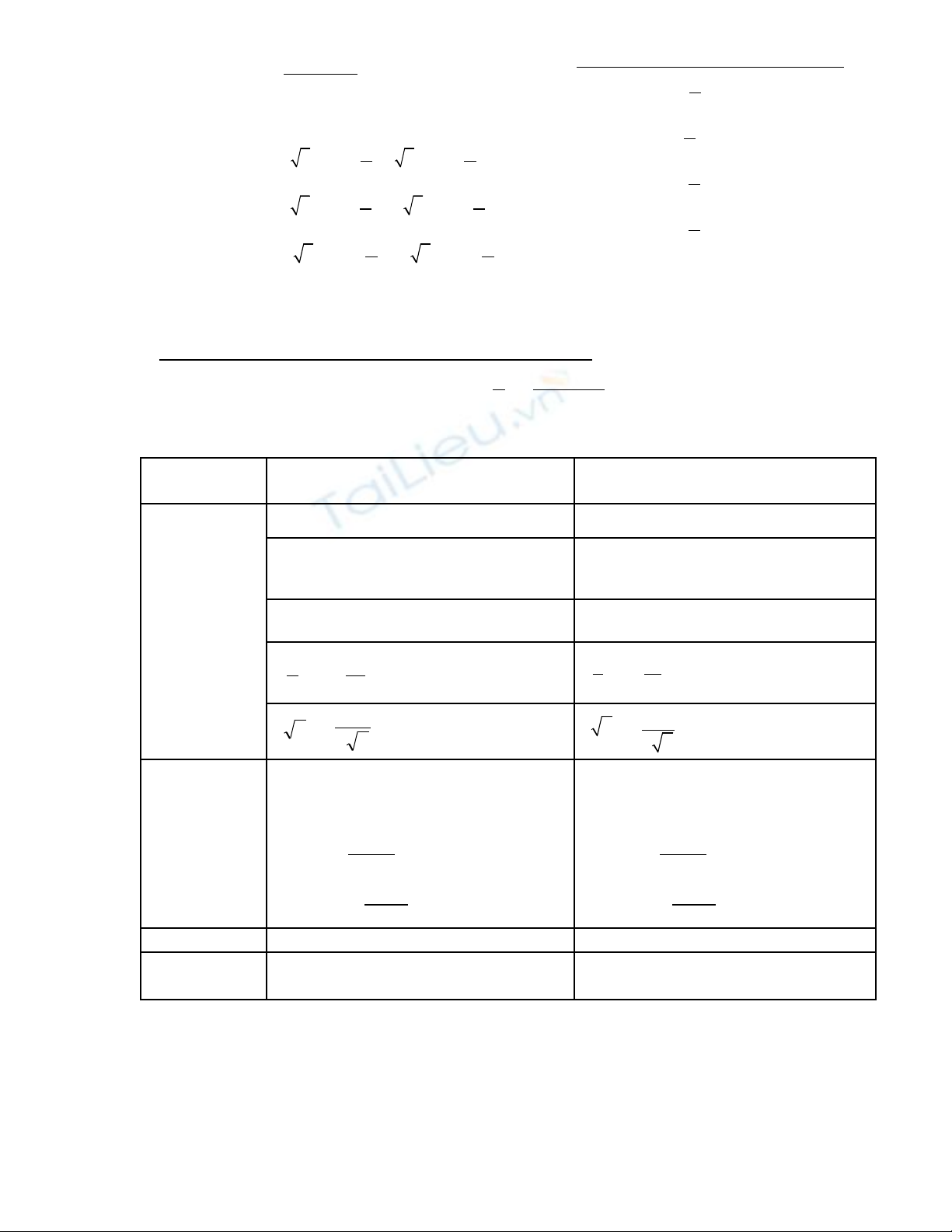
sin( )
cot cot ( , , )
sin .sin
− +
− = ≠ ∈
a b
a b a b k k Z
a b
π
sin cos 2 sin( ) 2 ( )
4 4
+ = + = −
a a a cos a
π π
sin cos 2 sin( ) 2 ( )
4 4
− = − = − +
a a a cos a
π π
cos sin 2 ( ) 2 sin( )
4 4
− = + = − −
a a cos a a
π π
7. Công th c bi n đ i tích thành t ngứ ế ổ ổ
[ ]
[ ]
[ ]
[ ]
1
cos .cos cos( ) cos( )
2
1
sin .sin cos( ) cos( )
2
1
sin .cos sin( ) sin( )
2
1
sin .cos sin( ) sin( )
2
a b a b a b
a b a b a b
a b a b a b
b a a b a b
• = − + +
• = − − +
• = + + −
• = + − −
Đ O HÀMẠ
1/ Các quy t c tính đ o hàmắ ạ (Ký hi u U=U(x), V=V(x)).ệ
•
( )
U V U V
′′ ′
± = ±
•
( )
UV U V UV
′′ ′
= +
•
2
U U .V U.V
V V
′′ ′
−
=
•{f[U(x)]}/ =
u
f'
.
x
U′
2/ Các công th c tính đ o hàmứ ạ :
Teân hàm
s ốCông th c đ o hàm ứ ạ Đ o hàm c a hàm s h pạ ủ ố ợ
Các hàm số
th ng g pườ ặ
( )
′
C
=0 (C lµ h»ng sè)
( )
′
x
=1 (kx)’=k (k lµ h»ng
sè )
( )
′
n
x
=n.xn-1 (n
∈
N, n
≥
2)
( )
n
u′
=n.un-1.u/
2
1 1
x x
′
= −
(x
≠
0)
′
= −
/
2
1 u
uu
≠(u 0)
′
)( x
=
x2
1
(x>0)
( )
′=
/
u
u2 u
>(u 0)
Hàm số
l ng giácượ
( )
( )
( )
( )
( )
/
/
/2
2
/2
2
sin cos
cos sin
11 tan
cos
1
cot 1 cot
sin
x x
x x
tanx x
x
x x
x
=
= −
= = +
= − = − +
( )
( )
( )
( )
//
//
//
2
//
2
sin cos .
cos sin .
1
tan .
cos
1
cot .
sin
u u u
u u u
u u
u
u u
u
=
= −
=
= −
Hàm lũy th aừ(xα)/= α x α -1 (uα)/= α u α -1u/
Hàm s mũố(ex )’ = ex
(ax)’ = axlna
( eu)’ = u’ .eu
( au)’ = u’ .au.lna
2
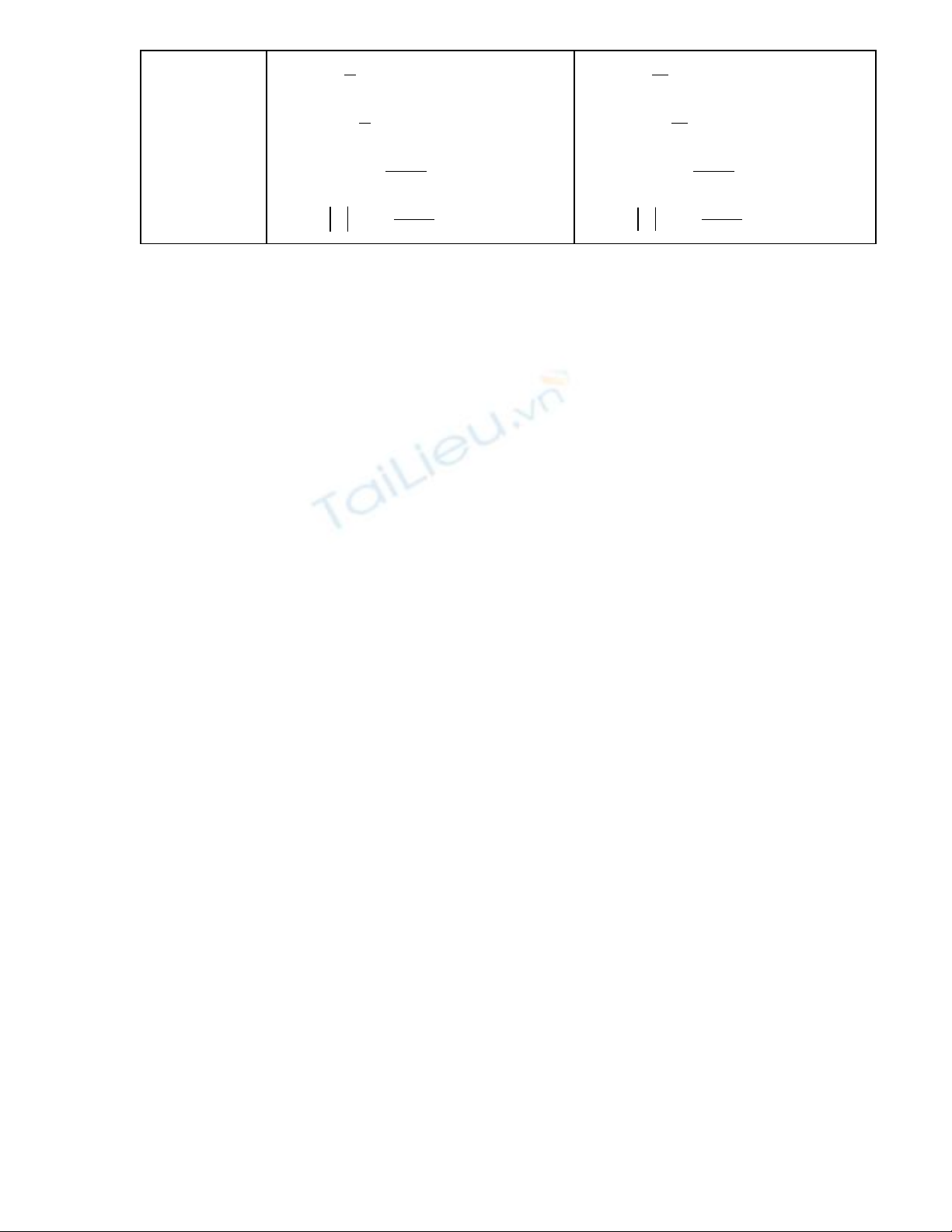
Hàm logarít (lnx )’ =
1
x
(x>0)
(ln /x/ )’ =
1
x
(x≠0)
(
log
a
x
)’ =
1
lnx a
(x>0, 0<a≠1)
(
log
a
x
)’ =
1
lnx a
(x>0, 0<a≠1)
( lnu)’ =
'u
u
(u>0)
( ln /u/ )’ =
'u
u
(u≠0)
(
log
a
u
)’ =
'
ln
u
u a
(u>0, 0<a≠0)
(
log
a
u
)’ =
'
ln
u
u a
(u>0, 0<a≠0)
3