1
ĐẠI HỌC QUỐC GIA HÀ NỘI
TRƯỜNG ĐẠI HỌC KHOA HỌC TỰ NHIÊN
ĐÁP ÁN VÀ THANG ĐIỂM
ĐỀ THI KẾT THÚC HỌC PHẦN, HỌC KỲ I, NĂM HỌC 2016-2017
Tên học phần:
PHƯƠNG PHÁP TOÁN CHO VẬT LÝ 1
Mã học phần: PHY2201
Số tín chỉ: 3
Đề số: 1
Dành cho sinh viên lớp học phần: PHY2201
NỘI DUNG ĐÁP ÁN
THANG
ĐIỂM
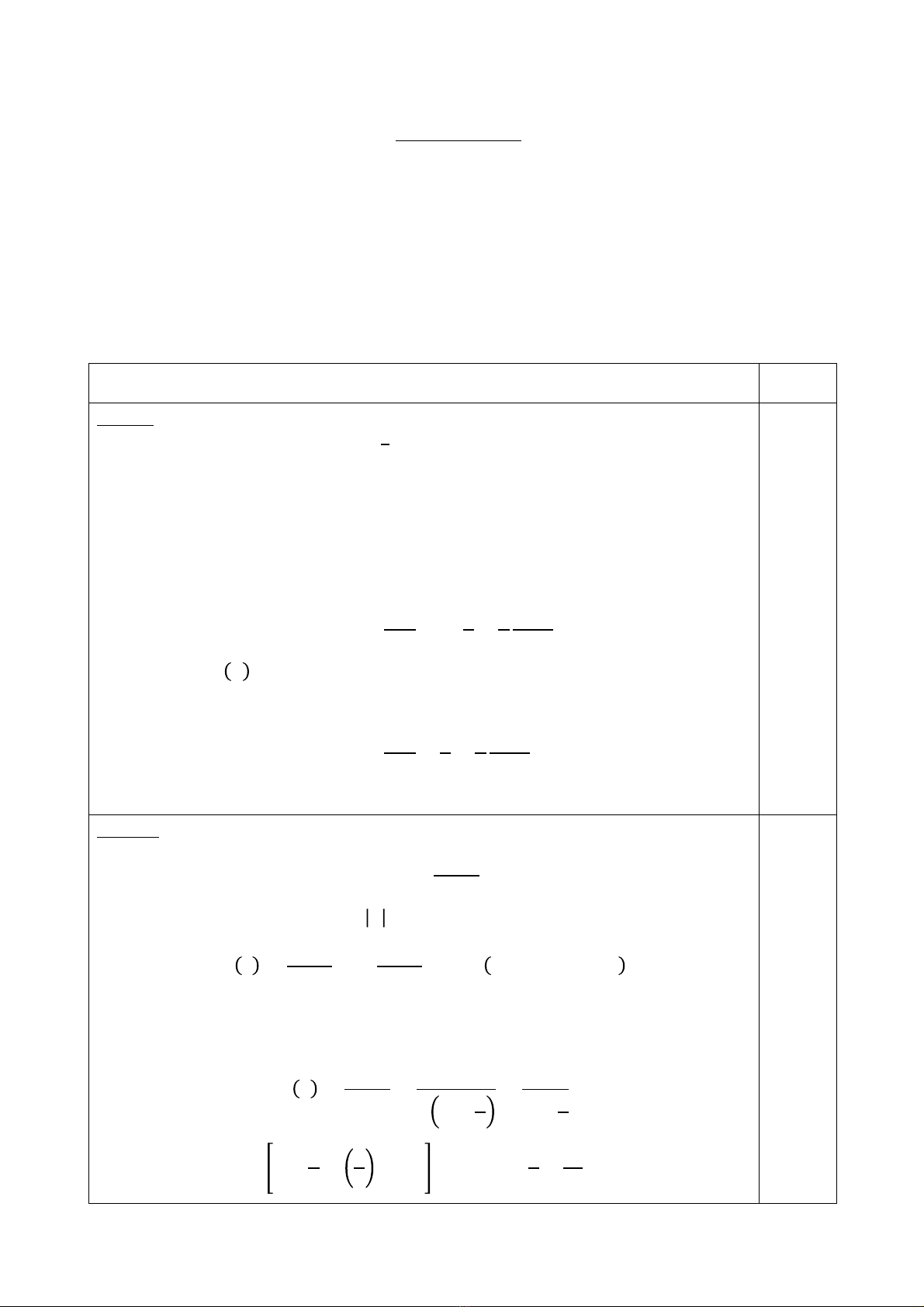
Câu 1: (3 điểm)
Phương trình: 𝑥!𝑦′′ +3𝑥𝑦′+𝑦=!
!,(𝑥>0) (1)
Đặt 𝑥=𝑒!,(𝑥>0),⇒𝑡=ln 𝑥
Phương trình (1) trở thành: 𝑦!! +2𝑦!+𝑦=𝑒!! (2)
Nghiệm tổng quát phương trình (2) là: 𝑦(𝑡)=𝐶!𝑡𝑒!!+𝐶!𝑒!!+(1/2)𝑡!𝑒!!
Nghiệm tổng quát phương trình (1) là:
𝑦(𝑥)=𝐶!
ln 𝑥
𝑥+𝐶!
1
𝑥+
1
2
ln!𝑥
𝑥
Từ điều kiện : 𝑦1=1⇒𝐶!=1; 𝑦′(1)=0⇒𝐶!=1
Nghiệm của bài toán là:
𝑦(𝑥)=
ln 𝑥
𝑥+
1
𝑥+
1
2
ln!𝑥
𝑥
1đ
1đ
1đ
Câu II: (2 điểm)
𝑓(𝑧)=
𝑧!
𝑧−1
a)Trong lân cận điểm z = 0, ta có 𝑧<1.
𝑓𝑧=
𝑧!
𝑧−1=−
𝑧!
1−𝑧
=−𝑧!1+𝑧+𝑧!+...
=−𝑧!−𝑧!−𝑧!−...
b) Trong lân cận điểm 𝑧=∞, ta có,
𝑓𝑧=
𝑧!
𝑧−1=
𝑧!
𝑧1−1
𝑧
=
𝑧
1−1
𝑧
=𝑧1+
1
𝑧+
1
𝑧
!
+...=𝑧+1+
1
𝑧+
1
𝑧!+...
1đ
1đ
TailieuVNU.com
2
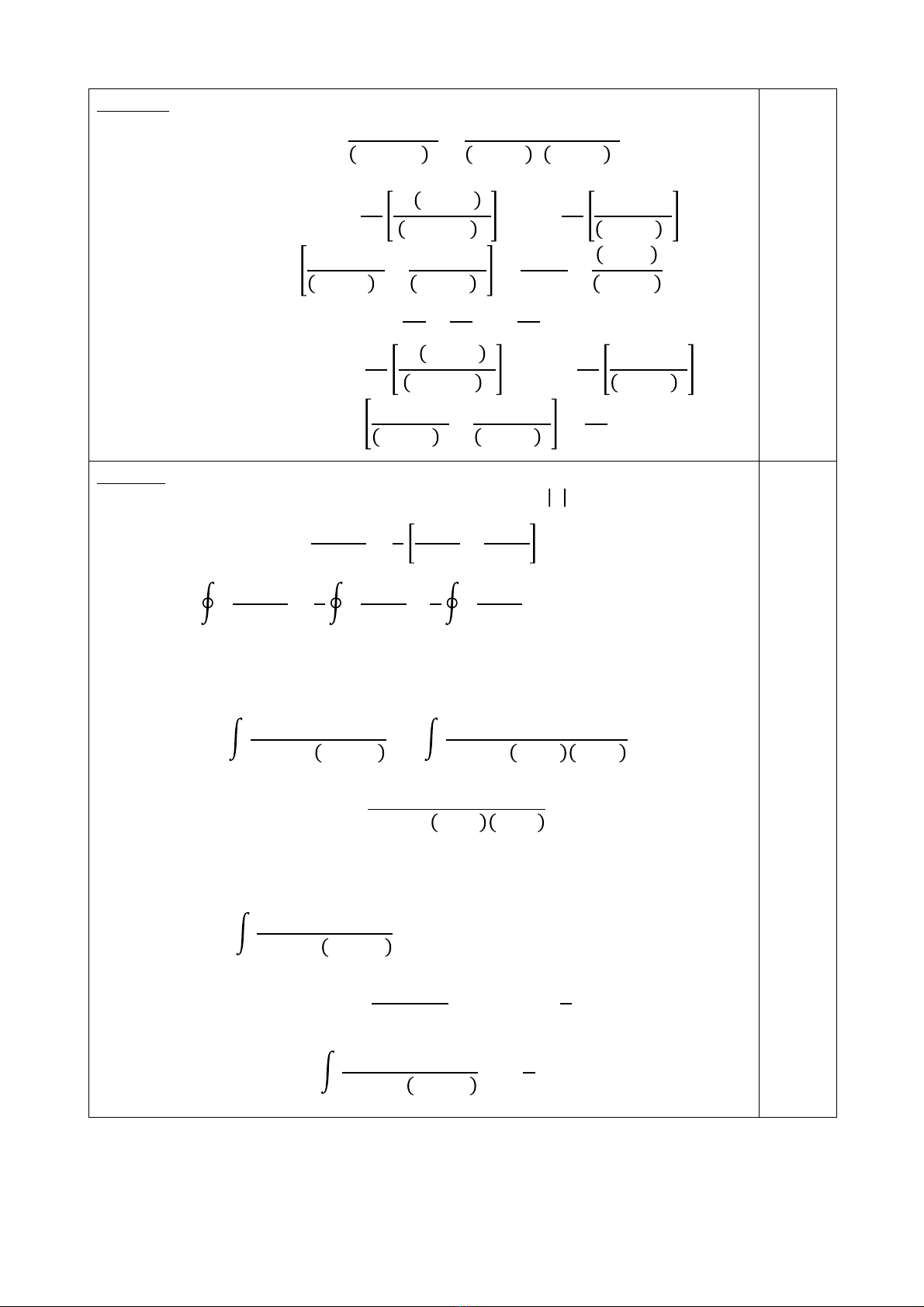
Câu II1: (2 điểm)
𝑓(𝑧)=
𝑧!
𝑧!+𝑎!!=
𝑧!
𝑧+𝑖𝑎 !𝑧−𝑖𝑎 !
Hàm f(z) có hai điểm cực cấp hai tại 𝑧=±𝑖𝑎.
res
!!!" 𝑓(𝑧)=lim
!→!"
𝑑
𝑑𝑧
𝑧!𝑧−𝑖𝑎 !
𝑧!+𝑎!!=lim
!→!"
𝑑
𝑑𝑧
𝑧!
𝑧+𝑖𝑎 !
=lim
!→!"
2𝑧
𝑧+𝑖𝑎 !−
2𝑧!
𝑧+𝑖𝑎 !=
2𝑖𝑎
−4𝑎!−
−2𝑎!
−8𝑖𝑎!
=−
𝑖
2𝑎+
𝑖
4𝑎
=−
𝑖
4𝑎
res
!!!!" 𝑓(𝑧)=lim
!→!!"
𝑑
𝑑𝑧
𝑧!𝑧+𝑖𝑎 !
𝑧!+𝑎!!=lim
!→!!"
𝑑
𝑑𝑧
𝑧!
𝑧−𝑖𝑎 !
=lim
!→!!"
2𝑧
𝑧−𝑖𝑎 !−
2𝑧!
𝑧−𝑖𝑎 !=
𝑖
4𝑎
1đ
1đ
Câu IV: (3 điểm)
a) Có hai điểm kỳ dị 𝑧=±1 nằm trong đường tròn C: z=2.
1
𝑧!−1=
1
2
1
𝑧−1−
1
𝑧+1
𝑑𝑧
𝑧!−1
!
=
1
2
𝑑𝑧
𝑧−1
!
−
1
2
𝑑𝑧
𝑧+1
!
=𝜋𝑖 −𝜋𝑖 =0
Công thức tích phân Cauchy.
b)
𝑑𝑥
(𝑥−1)𝑥!+1
!
!!
=
𝑑𝑥
(𝑥−1)𝑥+𝑖𝑥−𝑖
!
!!
𝑓(𝑧)=
1
(𝑧−1)𝑧+𝑖𝑧−𝑖
Trong nửa mặt phẳng phía trên trục thực có điểm cực đơn z = i và điểm cực đơn
z = 1 nằm trên trục thực.
𝑃
𝑑𝑥
(𝑥−1)𝑥!+1
!
!!
=2𝜋𝑖 res
!!!𝑓(𝑧)+𝜋𝑖 res
!!!𝑓(𝑧)
res
!!!𝑓(𝑧)=
1
2𝑖(𝑖−1); res
!!!𝑓(𝑧)=
1
2
𝑑𝑥
(𝑥−1)𝑥!+1
!
!!
=−
𝜋
2
0,5đ
1đ
0,5đ
0,5đ
0,5đ
Hà Nội, ngày 19 tháng 12 năm 2016
NGƯỜI LÀM ĐÁP ÁN
TailieuVNU.com