OLYMPIC C H C TOÀN QU C L N TH XXIII NĂM 2011Ơ Ọ Ố Ầ Ứ

ĐÁP ÁN MÔN NGUYÊN LÝ MÁY
Bài I (30 đi m /40)ể
1a. (3 đi m)ể
Chuy n đ ng c a khâu ch th p 2 làể ộ ủ ữ ậ
chuy n đ ng (song) ph ng, ể ộ ẳ xác đ nhị b iở
•Chuy n đ ng t nh ti n ể ộ ị ế theo đi m C trênể
vòng tròn ngo i ti p tam giác vuông gócạ ế
ACB, có tâm I trên đ ng kính ườ AB, v i v nớ ậ
t c ố
C
v
⊥
IC,
vC = lIC ωIC = lIC(
ϕ
2
) = dω1. (1)
•Chuy n đ ng quay ể ộ t ng đ iươ ố quanh tr c ụCz
v i v n t c gócớ ậ ố ω1 = const.
1b. (7 đi m)ể d)
Ph ng pháp h a đươ ọ ồ :
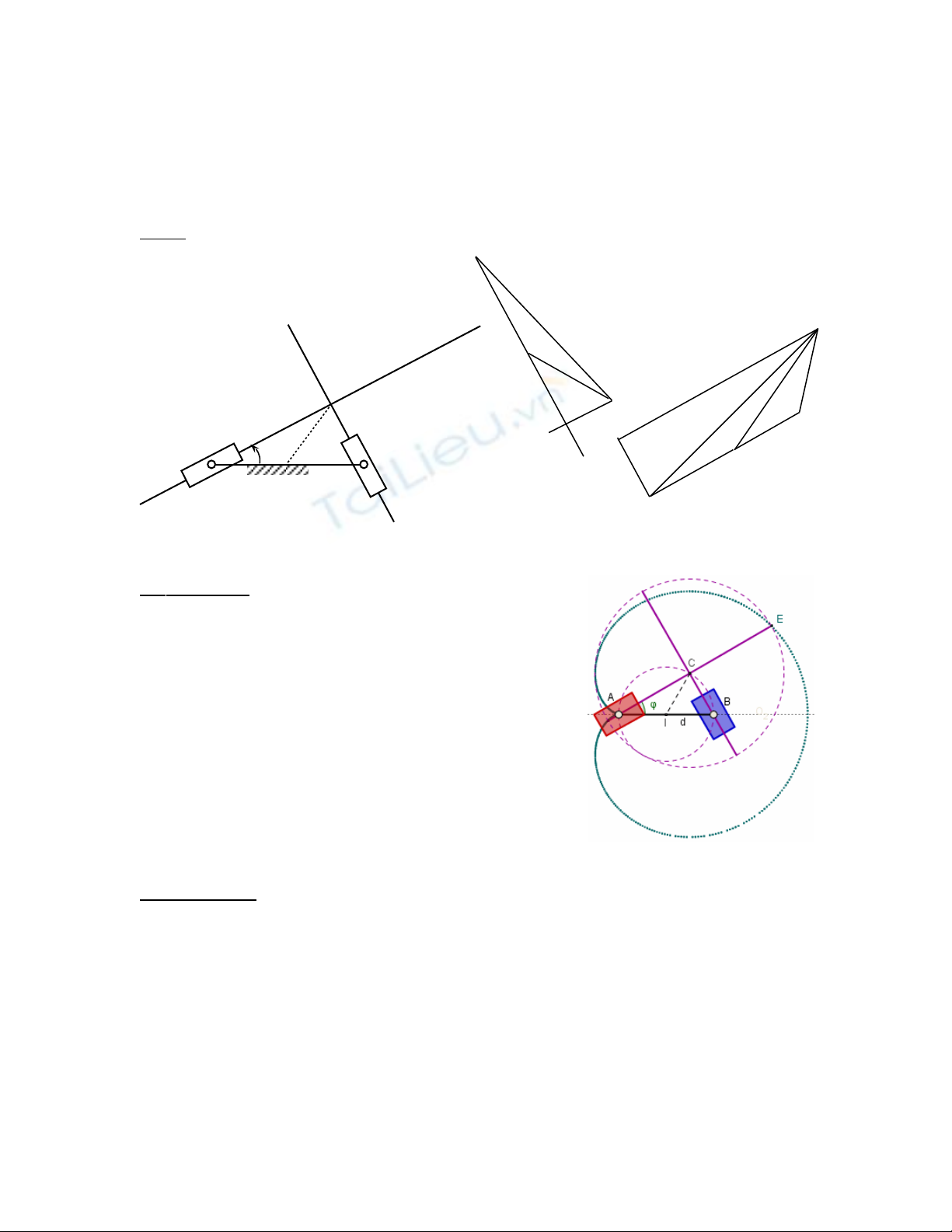
•Quĩ đ oạ c a đi m ủ ể E là đ ng hình tim ườ cardioid (hình 1d), d ng hìnhự
theo t a đ đ c c cọ ộ ộ ự (ρ, φ) : v đo n ẽ ạ
AE = AC+CE = ρ = d(cos φ + 1) (2)
ng v i m i giá tr ứ ớ ỗ ị φ ch n tr c.ọ ướ
(V vòng tròn ẽ(C,d) có tâm C và bán kính CE = d, d th y vòng trònễ ấ
này ngo i ti p v i quĩ đ o c a đi m ạ ế ớ ạ ủ ể C – là vòng tròn (I,d/2) – t i tâmạ
v n t c t c th i ậ ố ứ ờ P24 c a khâu 2, quĩ đ o c a ủ ạ ủ E vì th là m t tr ngế ộ ườ
a)b)c)
C
I
φ
d4
e’
n’
1
E
e
c
a
AB
2
3
1
Hình 1
pv
pa
c’
a’
h p đ c bi t c a đ ng epicycloid khi vòng tròn (ợ ặ ệ ủ ườ C,d) lăn không tr tượ
ngoài vòng tròn (I, d/2).
•V ẽh a đ v n t cọ ồ ậ ố (hình 1a) theo ph ng trình vect :ươ ơ
ECCE
vvv
+=
(3)
trong đó :
C
v
đã bi t (1), ế
CEv
EC
×=
1
ω
(vEC = dω1)
•V ẽh a đ gia t cọ ồ ố (hình 1c) theo ph ng trình vect :ươ ơ
t
EC
n
ECcE
aaaa
++=
(4)
trong đó
n
CIC
aa
=
theo h ng ướ CI,
2
d
a
n
CI
=
(2ω1)2 =
( ng v i đo nứ ớ ạ
pac’)
n
EC
a
theo h ng ướ EC,
2
1
ω
da
n
EC
=
( ng v i đo nứ ớ ạ
c’e’)
0
=
t
EC
a
vì ω1 = const.
Ph ng pháp gi i tíchươ ả :
V i bài toán này ph ng pháp ớ ươ t a đ đ c c cọ ộ ộ ự thích h p h n v nhi uợ ơ ề ề
m t so v i ph ng pháp ặ ớ ươ t a đ đêcac.ọ ộ
Ph ng trình chuy n đ ngươ ể ộ c a đi m ủ ể E trong h t a đ đ c c c (A,ệ ọ ộ ộ ự ρ,φ)
là
ρ(t) = d(1+cos ω1t)
φ(t) = ω1t
Quĩ đ oạ c a đi m E trong h t a đ này đ c mô t b i ph ng trình (2)ủ ể ệ ọ ộ ượ ả ở ươ
ρ = ρ(φ) = d(1+cosφ)
là đ ng cardioidườ .
V n t cậ ố
ϕρ
vvv
E
+=
(5)
trong đó
tdv
11
sin
ωωρ
ρ
−==
( ng v i đo n ứ ớ ạ pva trên hình 1b)
ρωϕρ
ϕ
==
v
( ng v i đo n ứ ớ ạ ae trên hình 1b)
Gia t cố
ϕρ
aaa
E
+=
(6)
trong đó
( )
ϕωϕρρ
ρ
2cos1
2
1
2
+−=−=
da
( ng v i đo n ứ ớ ạ pan’ trên hình 1c)
ϕωωϕρϕρ
ρϕ
sin222
2
11
dva
−==+=
( ng v i đo n ứ ớ ạ n’e’ trên hình
1c).
2a. (3 đi m)ể
Chuy n vể ị c a c n đ y ủ ầ ẩ
2
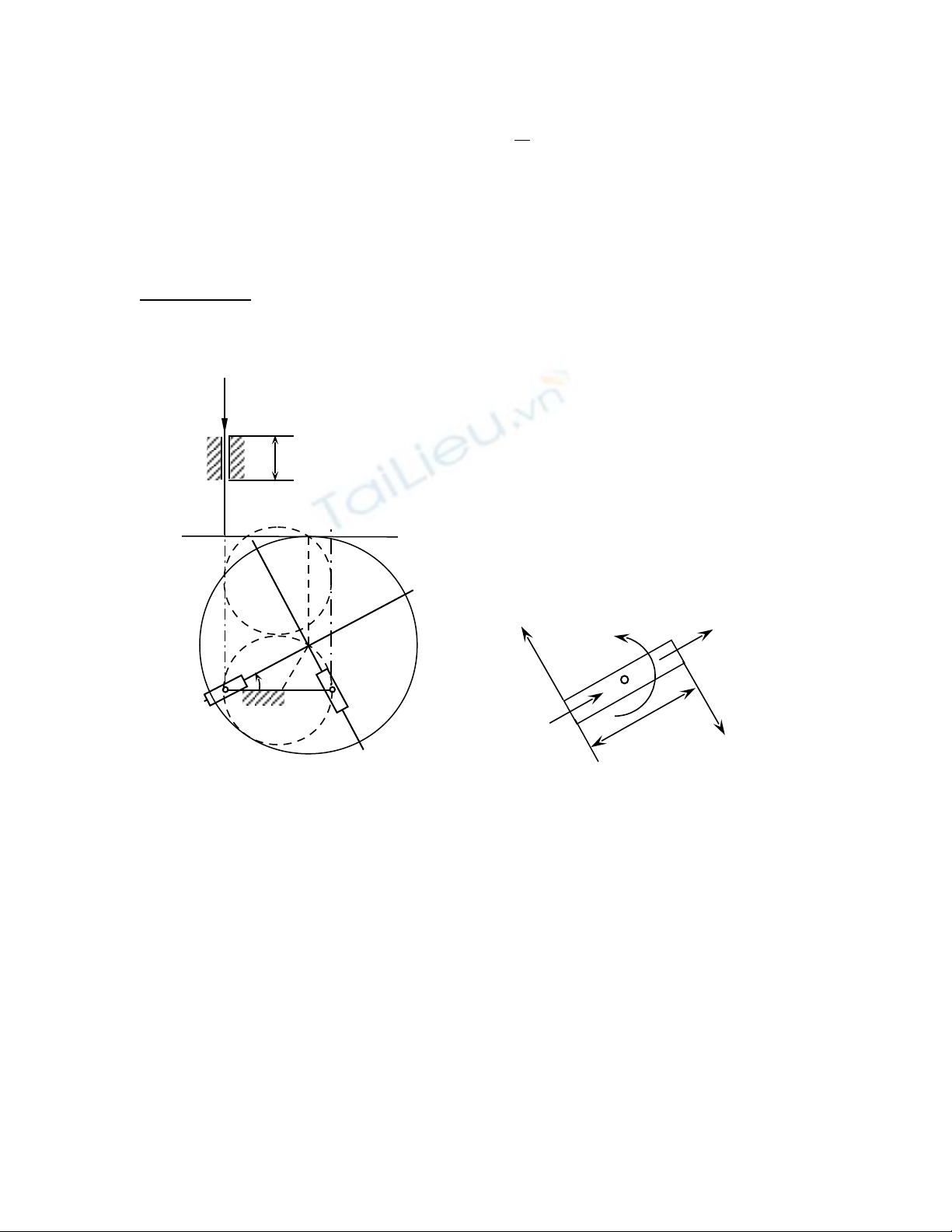
h5 = h5(φ,d) = lIC sin2φ + r2 =
2
2sin
2r
d+
ϕ
(7)
Hành trình c a c n đ y sau n a vòng quay c a khâu d n 1:ủ ầ ẩ ử ủ ẫ
H5 = d
V n t cậ ố c a c n đ y ủ ầ ẩ v5 = v5(φ,d) = ω1dcos2φ (8)
Gia t cố c a c n đ y ủ ầ ẩ a5 = a5(φ,d) = – 2
2
1
ω
dsin2φ (9)
2b. (4 đi m)ể
•Đ ng ăn kh pườ ớ : vì CT = r2 = const (đã cho), nên quĩ tích c a ti p đi mủ ế ể
T trong m t ph ng giá (đ ng ăn kh p) là v trí c a vòng tròn (ặ ẳ ườ ớ ị ủ I,d/2)
sau khi t nh ti n m t đo n ị ế ộ ạ CT = r2 .
•Biên d ng đ i ti p th cạ ố ế ự : c a cam là toàn biên d ng tròn (ủ ạ C,r2), c aủ
đáy c n là đo n th ng ầ ạ ẳ T’T” – hình chi u c a đ ng kính ế ủ ườ AB = d – trên
biên d ng lí thuy t.ạ ế
•V n t c tr t t ng đ i ậ ố ượ ươ ố :
V n t c tuy t đ i c a đi m ậ ố ệ ố ủ ể T trên biên d ng cam làạ
TCCT
vvv
+=
Hình chi u ế
t
T
v
c a ủ
T
v
trên T ’T ” cho phép xác đ nh v n t c tr t theoị ậ ố ượ
φ, ω1 và d :
t
T
v
= vCsin2φ + vTC = ω1(r2+2dsin2φ)
(10)
Hình 2
AB
C
E
φ
2
3
1d
T
4
5
Ka
Q
T”
T’
I
a)
Fms21’’
A
Fms21’
N21’ M1
b)
N21’’
a
3
2c. (3 đi m)ể
L c ma sát tr t ng c chi u v i v n t c tr t, có giá tr đ c xácự ượ ượ ề ớ ậ ố ượ ị ượ
đ nh b i áp l c liên k t ị ở ự ế N theo công th cứ
Fms = f N
T h a đ v n t c (hình 1b) và các công th c (8), (10) có th xác đ nhừ ọ ồ ậ ố ứ ể ị
các v n t c tr tậ ố ượ
v12 = vCsinφ = dω1sinφ, v32 = vCcosφ = dω1cosφ, (11)
v25 = ω1(r2+2dsin2φ) , v54 = ω1dcos2φ
T đi u ki n cân b ng momen c a các con tr t 1,3 và c n đ y 5 suyừ ề ệ ằ ủ ượ ầ ẩ
ra
Fms21 = 2f M1/a , Fms23 = 2f M3/a (12)
Fms45 = 2 fQd cos2φ/a, Fms25 = fQ
Đi u ki n cân b ng công su tề ệ ằ ấ c a c c u khi có ma sát tr t là ủ ơ ấ ượ
M1ω1 = M2ω2 + M3ω3+ Qv5 + Fms21v12 + Fms23v32 + Fms25v52 + Fms45v5 (13)
Thay các bi u th c (11),(12) vào (13) và chú ý r ng ể ứ ằ ω1= ω2= ω3 s suyẽ
ra bi u th c xác đ nh momen đ ng :ể ứ ị ộ
M1 = M1(Q, M2, M3, f, a, d, φ) (14)
3a. (5đi m)ể
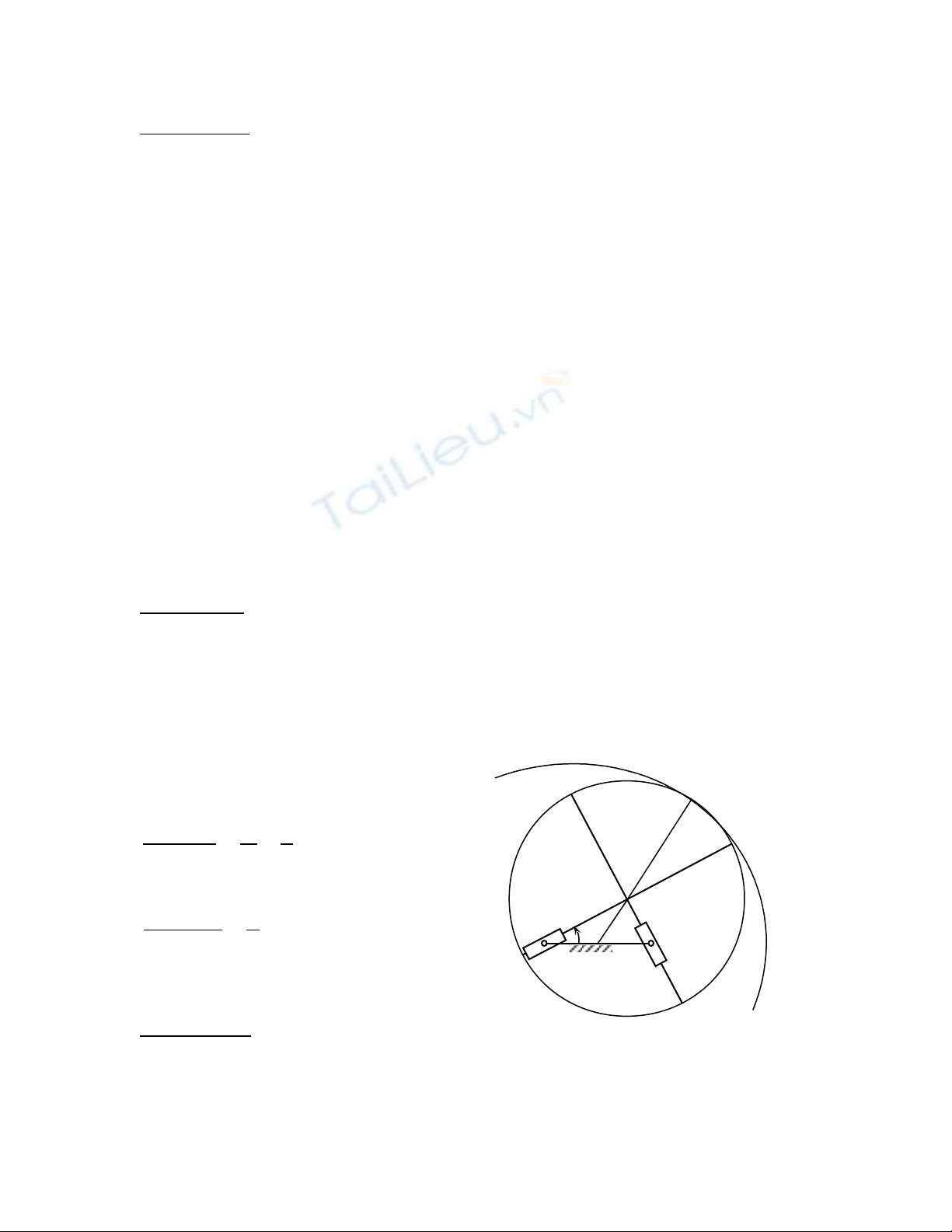
N u bánh răng ếr2 g n c ngắ ứ v i khâu ch th p 2 thì bánh răng nàyớ ữ ậ
chuy n đ ng song ph ng nh m t bánh răng v tinh có v n t c góc tuy tể ộ ẳ ư ộ ệ ậ ố ệ
đ i ốω2= ω1 , l pắ trên c n ầIC, v i ớωIC = 2ω1. V y bánh răng 6 ph i đ ngậ ả ồ
tr c v i c n ụ ớ ầ IC (t c là có tâm quay trùng v i ứ ớ I), và bán kính
r6 = IC + r2 = d/2
+ r2 = 6 cm (15)
V i h bánh răngớ ệ vi
sai n i ti p này:ộ ế
2
3
2
6
6
2
==
−
−
r
r
IC
IC
ωω
ωω
(16)
hay
2
3
2
16
1
=
−
−
ωω
ω
v y ậω6 =
4ω1/3 (17)
3b. (5 đi m)ể
N u bánh răng ếr2
không g n c ngắ ứ v iớ
4
AB
C
E
φ
2
31 d
4
6P
Hình 3
I
r2
khâu 2 thì ω2 ch a xác đ nh, c c u có hai b c t do , khi đó có th ch nư ị ơ ấ ậ ự ể ọ
ω2 và ω6 sao cho :
•C c u Onđam d ngơ ấ ừ , t c ứωIC = 0, ng v i tr ng h p c c u bánhứ ớ ườ ợ ơ ấ
răng th ng, mu n th ph i ch n :ườ ố ế ả ọ
ω2/ω6 = 3/2 (18)
•C c u Onđam đ o chi uơ ấ ả ề : v i ớω6 không đ i, ổthì ωIC = – kω6 (k > 0)
Khi đó theo công th c (16) :ứ
2
3
66
62
=
+
+
ωω
ωω
k
k
nghĩa là ph i ch n ả ọ ω2/ω6 = (3+k)/2 (19)
Bài II (10 đi m /40)ể
IIa. (3 đi m) ể
Khi khâu 1 là giá, ta đ c c c u sin, khâu ch th p 2 s chuy n đ ngượ ơ ấ ữ ậ ẽ ể ộ
t nh ti n v i lu tị ế ớ ậ
s2 = dsinθ (20)
IIb. (7 đi m)ể
Tâm v n t c t c th i ậ ố ứ ờ P24 trong chuy n đ ng t ng đ i gi a hai khâuể ộ ươ ố ữ
2,4 luôn là đi m đ i x ng v i ể ố ứ ớ C qua trung đi m ểI c a đo n ủ ạ AB. Quĩ tích
c a ủP24 trên khâu 4 là vòng tròn tâm tích T4 ngo i ti p hình ch nh tạ ế ữ ậ
ACBP24, trên khâu 2 là vòng tròn tâm tích T2 có tâm C và bán kính CP24 =
AB = d. Trong quá trình chuy n đ ng c a c c u sin, ể ộ ủ ơ ấ T4 (quay quanh A)
lăn không tr tượ v i ớT2 (t nh ti n theo ph ng ị ế ươ AC). C c u ma sát ho c cơ ấ ặ ơ
c u bánh răng v i c p vòng lăn t ng ng đ u th c hi n cùng m t lu tấ ớ ặ ươ ứ ề ự ệ ộ ậ
truy n đ ng nh c c u sin. Ngoài ra c c u cam ph ng v i ề ộ ư ơ ấ ơ ấ ẳ ớ
•cam là đĩa tròn 4 có tâm (hình h c) ọB và bán kính r b t kỳ, quay quanhấ
(tâm quay) A (còn g i là cam đĩa tròn l ch tâm, có ọ ệ tâm sai AB = d),
•c n đ y đáy b ng (2) vuông góc v i ph ng t nh ti nầ ẩ ằ ớ ươ ị ế
cũng th c hi n lu t truy n đ ng nh trên.ự ệ ậ ề ộ ư
5