1
OLYMPIC CƠ HỌC TOÀN QUỐC NĂM 2019
ĐỀ THI NGUYÊN LÝ MÁY
Bài I: [9.0 điểm]
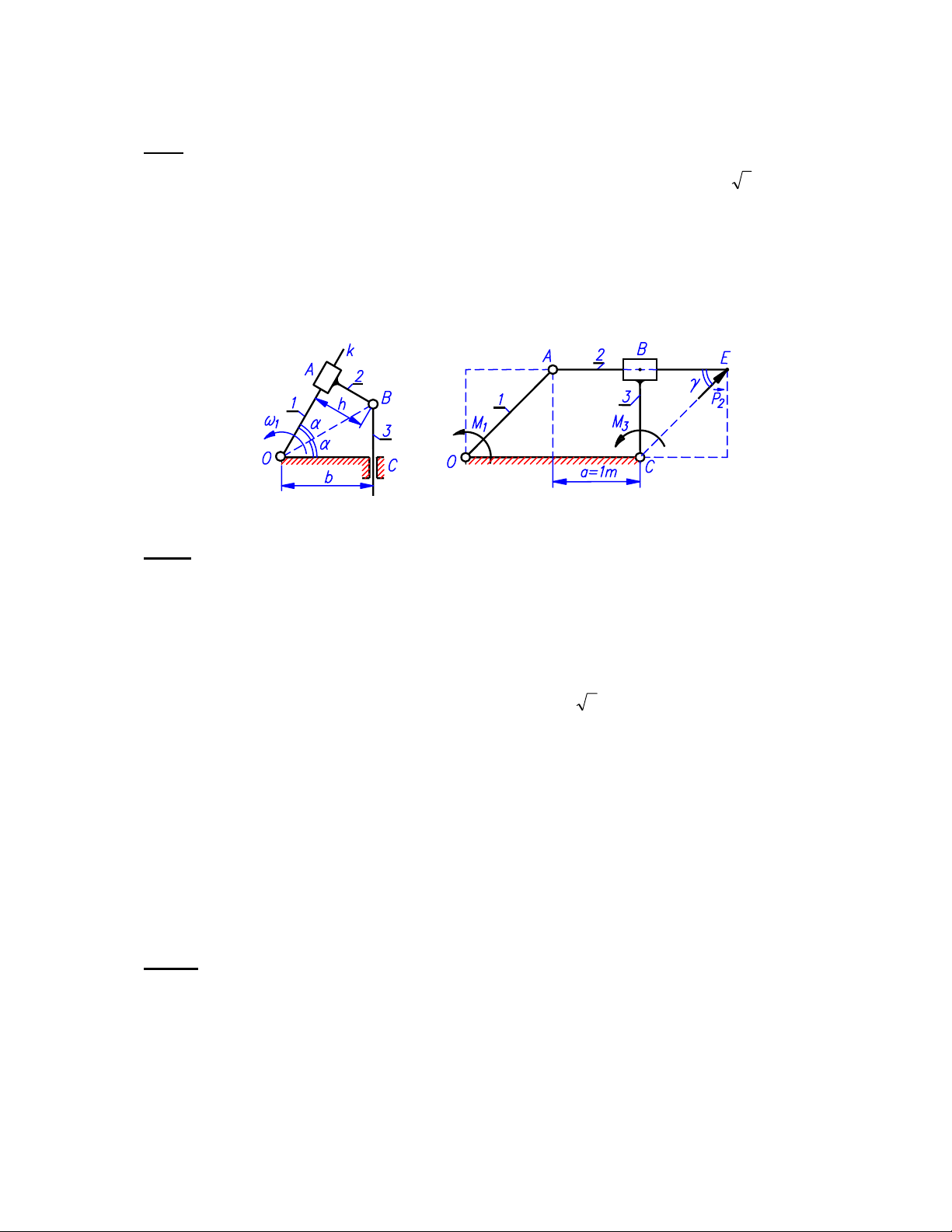
Cơ cấu 4 khâu OABC trên hình 1 có các kích thước động học đặc trưng b=3dm, h=1dm.
Tại vị trí khảo sát, tương ứng với các góc α=π/6, khâu 1 đang quay ngược chiều kim đồng
hồ với trị số vận tốc góc ω1=4rad/s.
1.1. Tìm vận tốc của khâu 3 tại vị trí đã cho.
1.2. Giả sử trị số và chiều của các vận tốc (dài hoặc góc) vẫn giữ nguyên như ở câu 1.1.
Hãy cho gia tốc góc của khâu 1 để khâu 3 chuyển động nhanh dần với gia tốc bằng 40dm/s2.
Hình 1. Hình 2.
Bài II: [11.0 điểm]
Cơ cấu phẳng OABC trên hình 2 (thuộc họ cơ cấu culit) có các kích thước động học và vị trí
khảo sát được cho theo lưới ô vuông, cạnh mỗi ô vuông nhỏ a=1m. Ngoại lực tác dụng gồm
mômen M1 trên khâu 1 trong vai trò mômen cân bằng, lực 2
P
G
đặt tại điểm E trên khâu 2 (E
trùng với đỉnh của một ô vuông nhỏ) và mômen M3 trên khâu 3. Lực 2
P
G
có đường tác dụng
tạo với đường thẳng AE góc γ=π/4 và có trị số P2=21000 N. Mômen M3 ngược chiều kim
đồng hồ và có trị số M3=2000Nm. Trọng lực và lực quán tính của các khâu được bỏ qua.
2.1. Tìm áp lực pháp tuyến tại 4 khớp động và giá trị 0
1
M của mômen M1 trong trường
hợp bỏ qua tất cả các lực ma sát.
2.2. Giả sử bỏ qua ma sát tại tất cả các khớp quay và ma sát với môi trường, chỉ tính
đến ma sát tại khớp tịnh tiến B. Đây là khớp tịnh tiến rãnh tròn, áp suất phân bố theo quy
luật côsin trên nửa mặt trụ tiếp xúc (hệ số phân bố áp suất λ=4/π), hệ số ma sát của cặp vật
liệu tạo khớp là f=π/25. Tính giá trị 1
1
M của mômen cân bằng M1 trong trường hợp này và
suy ra hiệu suất của cơ cấu ở vị trí đang xét.
Bài III: [6.0 điểm]
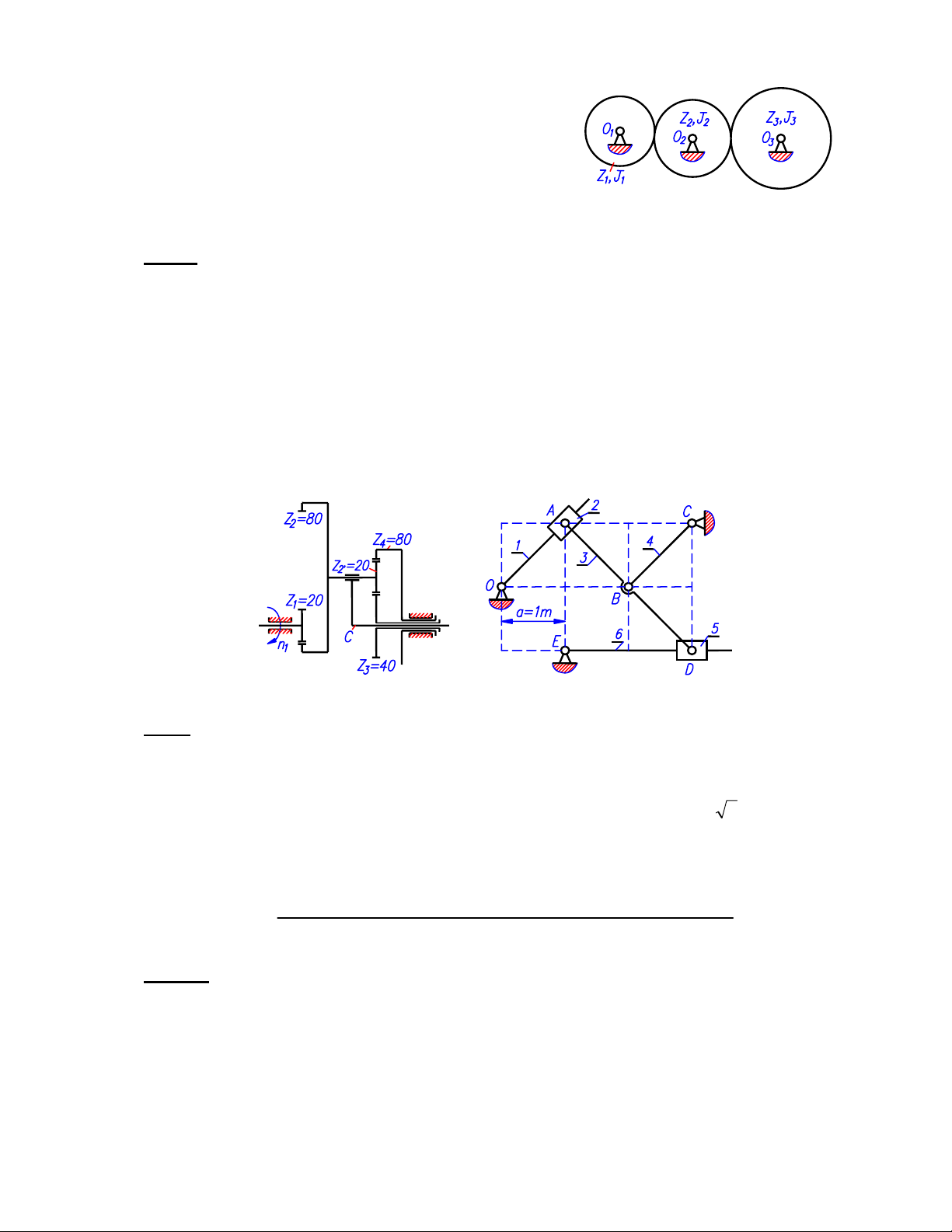
Trong hệ bánh răng trên hình 3, tất cả các cặp ăn khớp cùng thỏa mãn điều kiện ăn khớp
đúng, khối tâm của các bánh răng nằm trên trục quay tương ứng, bánh Z1 là khâu thu gọn.
Số răng của các bánh răng: Z1=20, Z2=25, Z3=32. Mômen quán tính khối lượng đối với trục
quay tương ứng của các khâu lần lượt là J1=1,20kg.m2, J2=1,25kg.m2, J3=1,28kg.m2.
Trên trục bánh Z1 tác dụng mômen phát động M1=1500Nm, trên trục bánh Z3 tác dụng
mômen cản M3=2000Nm (M1, M3 không vẽ trên hình), các lực ma sát được bỏ qua.
2
3.1. Tìm mômen quán tính khối lượng và mômen
lực thu gọn của cơ cấu.
3.2. Hãy tìm quy luật chuyển động của hệ thể
hiện qua gia tốc góc, vận tốc góc và chuyển vị góc
của bánh Z1, biết rằng vận tốc góc và chuyển vị góc
của bánh Z1 bằng 0 tại thời điểm ban đầu.
Bài IV: [8.0 điểm]
Xét hệ bánh răng với sơ đồ động và số răng của các bánh được thể hiện trên hình 4 (bánh Z4
không được vẽ đầy đủ). Biết bánh răng Z1 đang quay với tốc độ n1=1650 vòng/phút.
4.1. Tìm tốc độ quay theo vòng/phút của cần C khi cố định bánh răng Z4.
4.2. Tính tỷ số truyền từ bánh Z3 đến bánh Z4 khi cho cần C quay ngược chiều bánh Z1
với trị số tốc độ bằng một nửa (|n1|=2|nC|).
4.3. Tìm tốc độ quay tuyệt đối và tốc độ quay tương đối so với cần C của khối bánh
răng (Z2-Z2') trong trường hợp các bánh răng Z3 và Z4 quay ngược chiều nhau với cùng một
giá trị tốc độ.
Hình 4. Hình 5.
Bài V: [6.0 điểm]
Xét cơ cấu thanh phẳng OABCDE trên hình 5 với các kích thước động học và vị trí khảo sát
được cho trên lưới ô vuông, cạnh mỗi ô vuông nhỏ a=1m. Biết rằng khâu 2 đang chuyển
động so với khâu 1 theo chiều từ O đến A với trị số vận tốc tương đối V21=22 m/s và khâu 5
đang chuyển động so với khâu 6 theo chiều từ E đến D với trị số vận tốc tương đối
V56=1m/s. Hãy xác định vận tốc góc tuyệt đối (vận tốc góc so với giá) của các khâu động
thuộc cơ cấu.
HẾT
Ghi chú: Cán bộ coi thi không cần giải thích gì thêm.
Hình 3.
3
OLYMPIC CƠ HỌC TOÀN QUỐC NĂM 2019
ĐÁP ÁN MÔN NGUYÊN LÝ MÁY
Bài I: [9.0 điểm]
Có thể giải bài toán bằng phương pháp họa đồ vectơ, hoặc phương pháp giải tích.
a) Phương pháp họa đồ vectơ.
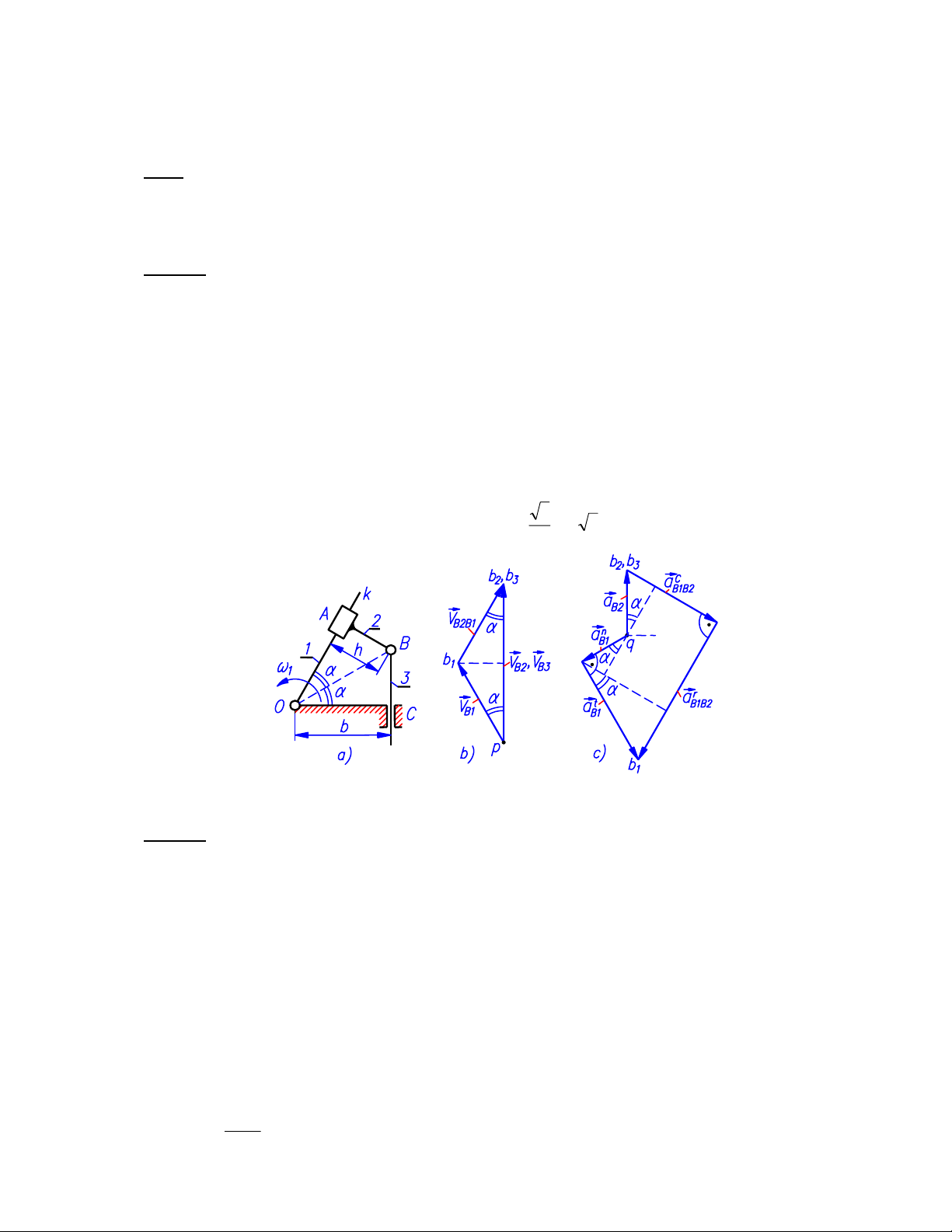
Câu 1.1: [4.00đ]
Trước hết, cần lưu ý rằng ω2 = ω1 = 4rad/s và lOB = b/cosα = 2(dm).
• Xét các trùng điểm B với quan hệ vận tốc:
1B2B1B2B3B VVVV
G
GGG +== (1.1)
//By ⊥OB //Ok
----- ω1lOB -----
(?) 8dm/s (?)
• Vẽ họa đồ vận tốc biểu diễn phương trình (1.1) như trên hình 1b.
• Theo họa đồ ta tính được:
VB2B1=VB1=8dm/s; VB3=VB2=38
2
3
.8.2cos.2 1B ==αV(dm/s)
Hình 1.1.
Câu 1.2: [5.00đ]
• Trong trường hợp này, ta đã biết 3B2B aa
G
G
=
. Vẫn xét các trùng điểm B, nhưng biểu diễn gia
tốc của điểm B1 theo gia tốc của điểm B2 (nhớ rằng 2B1B
V
G
ngược chiều 1B2B
V
G
):
r
2B1B
C
2B1B2B
t
1B
n
1B aaaaa
G
G
G
G
G
++=+ (1.2)
B→O ⊥OB //By 1B2B2
2V
G
G
×ω //Ok
OB
2
1lω ε1lOB ----- 1B2B2
2Vω -----
32 (?) 40dm/s2 64 (?)
• Họa đồ gia tốc biểu diễn phương trình (1.2) có dạng như trên hình 1c.
• Bằng cách dựng thêm một số đường kẻ phụ trên họa đồ, ta tính được:
α+α−=+α− cossinsin t
1B
n
1B
C
2B1B2B aaaa
)sinsin(
cos
1C
2B1B2B
n
1B
t
1B aaaa +α−α
α
=
4
⇒ 34064
2
1
.40
2
1
.32
3
2
t
1B =
⎟
⎠
⎞
⎜
⎝
⎛+−=a(dm/s2)
356
2
3
.40
2
3
.32
2
1
.340coscossin 2B
n
1B
t
1B
r
2B1B =++=α+α+α= aaaa (dm/s2)
• Suy ra gia tốc góc của khâu 1:
320
2
340
OB
t
1B
1===ε l
a(rad/s2) (ε1 thuận chiều kim đồng hồ)
Vậy, để thỏa mãn yêu cầu bài toán, cần cho gia tốc góc của khâu 1 với giá trị 320
rad/s2, thuận chiều kim đồng hồ.
b) Phương pháp giải tích.
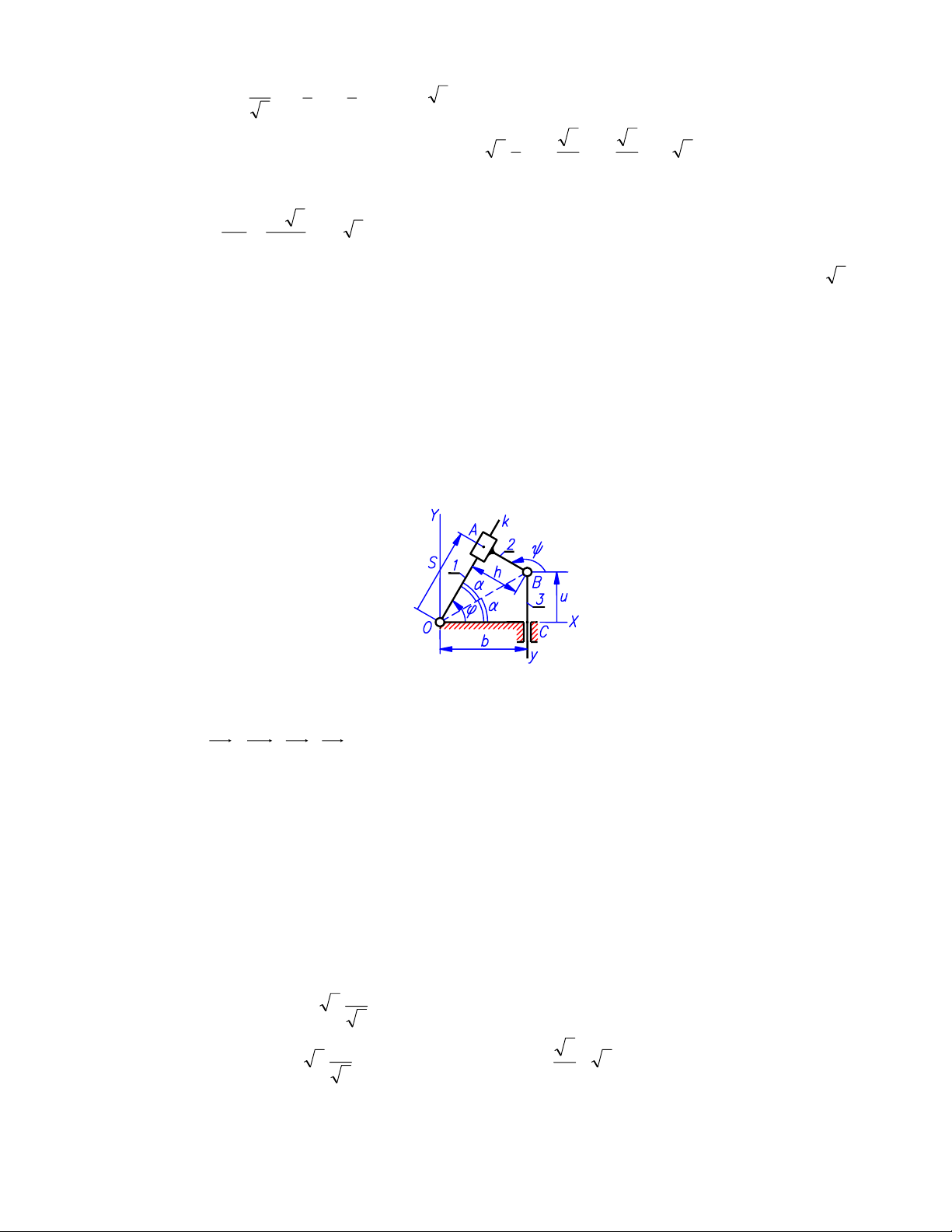
• Đầu tiên ta dựng hệ trục tọa độ OXY và ký hiệu chính xác A là chân đường vuông góc
hạ từ B xuống đường trượt Ok, C là giao của By với trục OX (hình 1.2).
Để mô tả chuyển động tuyệt đối và tương đối của các khâu, ta sử dụng các tọa độ suy
rộng ϕ, S, ψ và u. Quy ước chiều dương của ϕ, ψ là ngược kim đồng hồ, của S, u là chiều
mũi tên). Các thông số ϕ, u biểu diễn chuyển động tuyệt đối của khâu 1 và khâu 3, thông số
S biểu diễn chuyển động tương đối của khâu 2 so với khâu 1.
Hình 1.2.
• Tại vị trí bất kỳ, ta luôn có các quan hệ:
BACBOCOA ++= (1.3)
ψ = π/2 + ϕ (1.4)
Dạng hình chiếu của (1.3) trên hai trục tọa độ là:
⎩
⎨
⎧
ψ+=ϕ
ψ+=ϕ
sinsin
coscos
huS
hbS (1.5)
Thay (1.4) vào (1.5) ta được:
⎩
⎨
⎧
ϕ+=ϕ
ϕ−=ϕ
cossin
sincos
huS
hbS ⇔ ⎩
⎨
⎧
ϕ−ϕ=
ϕ
−
=
ϕ
cossin
sincos
hSu
hbS (1.6)
• Tại vị trí khảo sát (ứng với các góc α=π/6), ta có (hình 1.2):
lOB = b/cosα = 3
2
.3 = 2(dm); ϕ = 2α = π/3; ψ = π/2 + ϕ = 5π/6;
u = btanα = 3
1
.3 = 1(dm); S = lOBcosα = 3
2
3
.2 =(dm);
Theo giả thiết, tại vị trí khảo sát ta cũng có: 4
1
=
ω
=
ϕ
rad/s, 40
3
=
=
au
dm/s2.
• Để xác định các vận tốc ta đạo hàm hai vế các phương trình (1.5) theo thời gian.
5
Tại thời điểm bất kỳ, ta có:
⎩
⎨
⎧
ϕϕ+ϕϕ+ϕ=
ϕϕ−=ϕϕ−ϕ
sincossin
cossincos
hSSu
hSS (1.7)
Suy ra các vận tốc quan tâm tại thời điểm khảo sát:
84.13.4.3tan =−=ϕ−ϕϕ=
hSS (dm/s)
38
2
3
.4.1
2
1
.4.3
2
3
.8sincossin =++=ϕϕ+ϕϕ+ϕ=
hSSu (dm/s)
Theo đó, vận tốc tương đối của khâu 2 so với khâu 1 hướng từ O về A và có giá trị bằng
8dm/s, vận tốc của khâu 3 hướng từ dưới lên trên và có trị số bằng 38 dm/s.
• Để xác định các gia tốc ta đạo hàm hai vế các phương trình (1.7) theo thời gian.
Tại thời điểm bất kỳ ta có:
⎩
⎨
⎧
ϕϕ+ϕϕ+ϕϕ−ϕϕ+ϕϕ+ϕ=
ϕϕ+ϕϕ−=ϕϕ−ϕϕ−ϕϕ−ϕ
cossinsincoscos2sin
sincoscossinsin2cos
22
22
hhSSSSu
hhSSSS (1.8)
Thay các giá trị đã biết tương ứng với vị trí đang xét vào (1.8) ta nhận được hệ:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+ϕ+−ϕ++=
+ϕ−=−ϕ−−
2
1
.4.1
2
3
..1
2
3
.4.3
2
1
..3
2
1
.4.8.2
2
3
.40
2
3
.4.1
2
1
..1
2
1
.4.3
2
3
..3
2
3
.4.8.2
2
1
22
22
S
S
⇔ ⎪
⎩
⎪
⎨
⎧
=ϕ+
=ϕ−
3162
3962
S
S ⇒ ⎪
⎩
⎪
⎨
⎧
−=ϕ
=
)(rad/s320
)(dm/s356
2
2
S
Theo đó, cần phải cho gia tốc góc của khâu 1 quay cùng chiều kim đồng hồ với trị số
bằng 320 rad/s2.
Các kết quả nhận được theo hai phương pháp hoàn toàn trùng nhau.