1
OLYMPIC CƠ HỌC TOÀN QUỐC NĂM 2023
ĐỀ THI NGUYÊN LÝ MÁY
Bài I: [15.0 điểm](9.0+6.0)
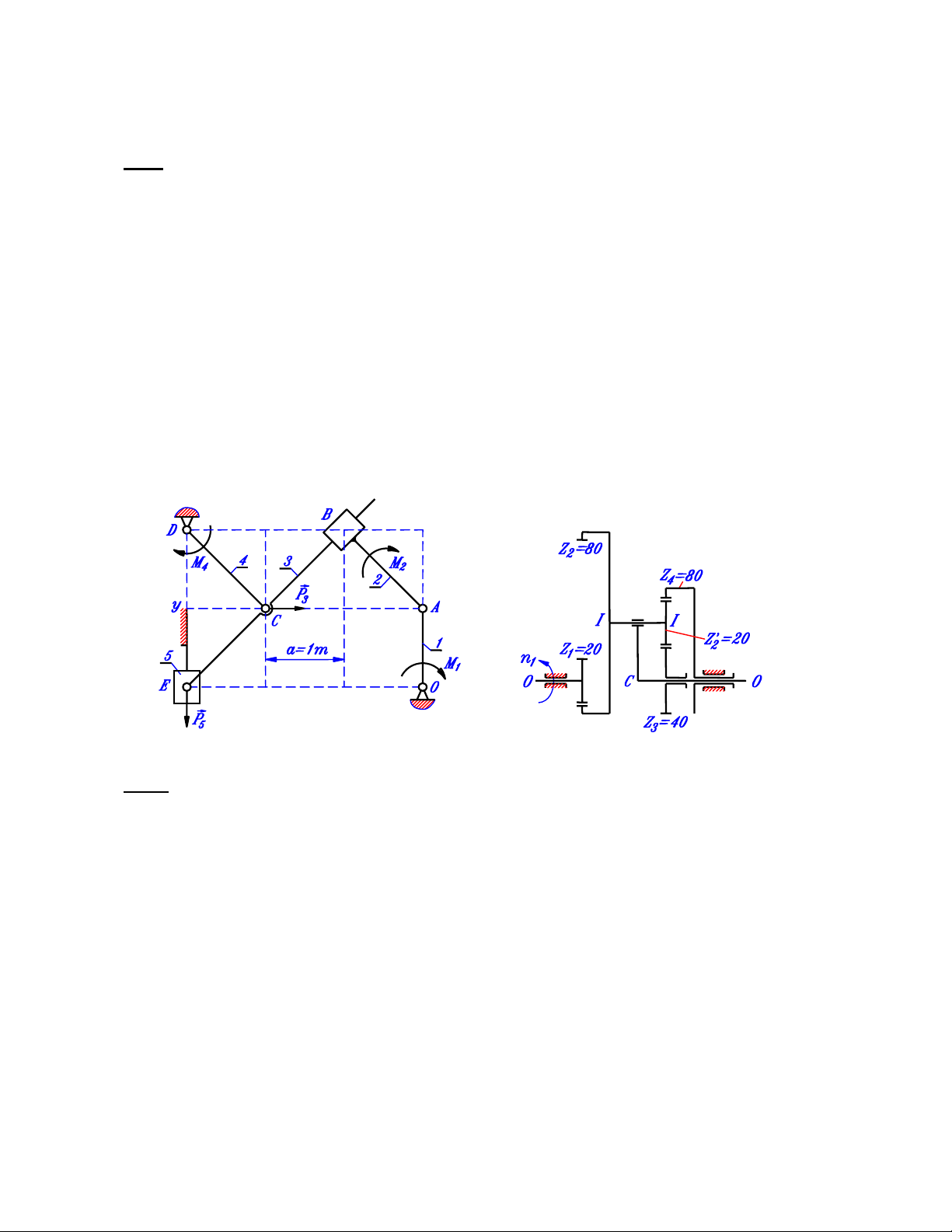
Cơ cấu phẳng OABCDE có các kích thước động học và vị trí khảo sát được cho trên lưới ô
vuông như trên hình 1. Giả sử các khâu của cơ cấu cân bằng dưới tác dụng của hệ lực và
mômen chủ động {M1, M2, 3
P
G
, M4, 5
P
G
} có chiều như thể hiện trên hình. Các mômen M1, M2, M4
cùng chiều kim đồng hồ. Lực 3
P
G
nằm ngang, hướng sang phải và đi qua tâm quay C. Lực 5
P
G
thẳng đứng, hướng xuống dưới và đi qua tâm quay E. Bỏ qua ma sát, trọng lực và lực quán tính
của các khâu. Biết trị số của các lực và mômen là: M2=2000Nm, P3=2000N, M4=2000Nm,
P5=3000N.
1.1. Tính áp lực tại các khớp động và mômen M1 trong vai trò mômen cân bằng.
1.2. Giả sử mômen M1 có trị số 1000Nm, lực 3
P
G
đặt tại điểm K nào đó trên khâu 3 thay vì
đặt tại điểm C, thông tin còn lại của các lực và mômen vẫn giữ nguyên như trước. Tìm tập hợp
các vị trí của điểm K trên khâu 3 (mở rộng) sao cho các khâu của cơ cấu cân bằng dưới tác dụng
của hệ lực và mômen đã cho.
Hình 1. Hình 2.
Bài II: [10.0 điểm](4.00+6.00)
Xét hệ bánh răng với sơ đồ động học và số răng của các bánh được thể hiện như trên hình 2.
Hệ có 3 khối bánh răng vệ tinh Z2-Z'2 giống hệt nhau được bố trí cách đều nhau theo góc 1200.
Khối tâm của các bánh răng Z1, Z3, Z4 và cần C nằm trên trục trung tâm O-O, khối tâm của mỗi
khối bánh răng vệ tinh nằm trên trục quay riêng I-I của nó. Ký hiệu tốc độ quay theo vòng/phút
của bánh răng Zj là nj (j=1÷4), của cần C là nC. Bánh răng Z1 đang quay theo một chiều xác định
với tốc độ n1=1800 vòng/phút.
2.1. Tìm tốc độ và chiều quay của cần C trong hai trường hợp độc lập sau:
a) Cố định bánh răng Z3. b) Cố định bánh răng Z4.
2.2. Tính mômen quán tính khối lượng thu gọn của hệ về trục quay của bánh răng Z1 trong
trường hợp cần C quay cùng chiều bánh răng Z1 với tốc độ bằng 1/10 lần tốc độ của bánh Z1.
Cho bán kính mặt trụ đi qua đường tâm trục của 3 khối bánh răng vệ tinh rC=20cm; khối lượng
của một khối bánh răng vệ tinh m2=10kg; mômen quán tính khối lượng của mỗi khối bánh răng
vệ tinh đối với trục quay riêng JS2=6,40kg.m2, của các bánh răng Z1, Z3, Z4 và cần C đối với trục
trung tâm O-O lần lượt là JS1=1,3025kg.m2, JS3=3,20kg.m2, JS4=5,12kg.m2, JC=3,20kg.m2.
2
Bài III: [15.0 điểm](11.0+4.0)
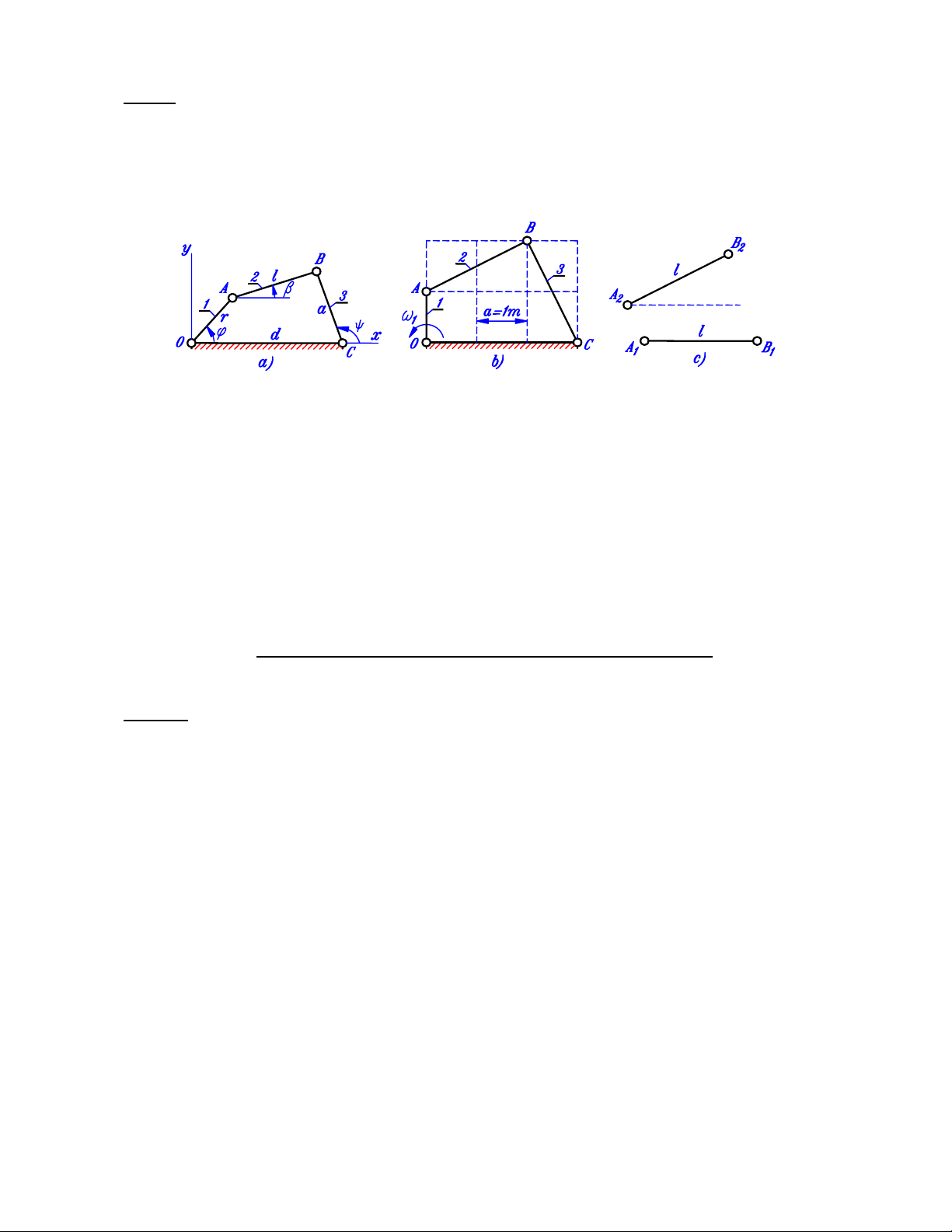
Cơ cấu 4 khâu bản lề phẳng OABC với các kích thước hình học đặc trưng r=OA, l=AB, a=BC,
d=OC chuyển động trong mặt phẳng tọa độ Oxy (trục Ox trùng với đường giá OC) như thể hiện
trên hình 3a. Gọi ϕ, β, Ψ lần lượt là góc tạo bởi các tia OA, AB, CB với chiều dương của trục
Ox (ϕ, β, Ψ được gọi là góc định vị của khâu 1, khâu 2 và khâu 3).
Hình 3.
3.1. Xét cơ cấu với các kích thước hình học và vị trí khảo sát được cho trên lưới ô vuông
như hình 3b. Tại vị trí khảo sát, khâu 1 đang quay ngược chiều kim đồng hồ với trị số vận tốc
góc không đổi ω1=10rad/s.
a) Xác định vận tốc góc, gia tốc góc của khâu 2 và khâu 3 bằng phương pháp họa đồ.
b) Hãy sử dụng phương pháp giải tích để kiểm tra lại các kết quả đã nhận được ở trên.
3.2. Giả sử đã biết các kích thước r, l và hai vị trí A1B1, A2B2 của thanh truyền AB như thể
hiện trên hình 3c (coi hình vẽ được biểu diễn với tỷ lệ xích bằng 1 và 2r>A1A2). Trình bày cách
xác định các kích thước a và d bằng phương pháp vẽ, biết rằng khi tia OA đi qua trung điểm của
đoạn thẳng A1A2 thì tia CB cũng đi qua trung điểm của đoạn thẳng B1B2.
HẾT
Ghi chú: Cán bộ coi thi không cần giải thích gì thêm.
3
OLYMPIC CHTQ NĂM 2023
ĐÁP ÁN MÔN NGUYÊN LÝ MÁY
Bài I: [15.0 điểm]
Câu 1.1: [10.0 điểm]
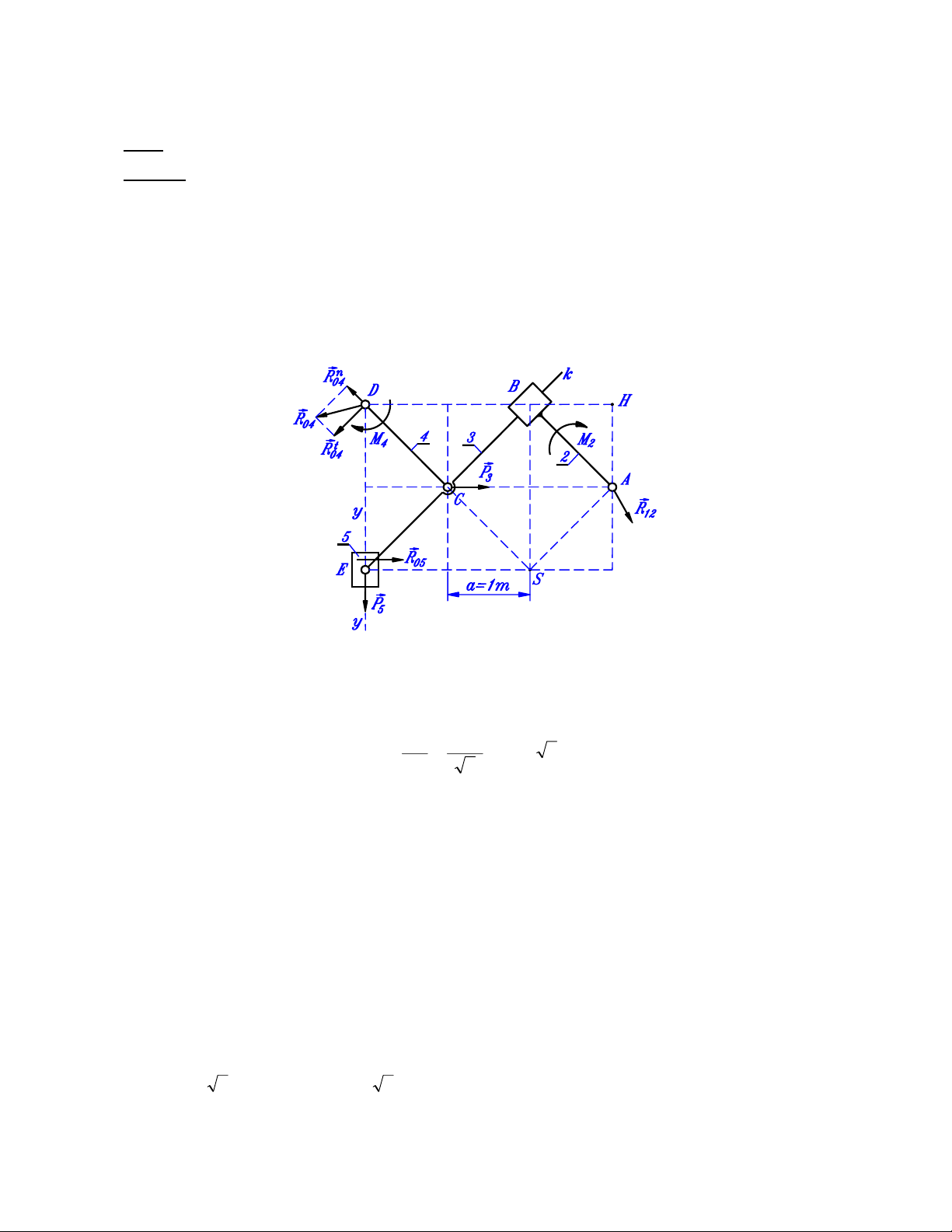
a) Xét cân bằng của nhóm Axua gồm các khâu 2, 3, 4 và 5 như trên hình 1.1.
• Hệ lực tác dụng trên nhóm gồm:
+ Hệ lực và mômen chủ động {M2, 3
P
G
, M4, 5
P
G
};
+ Phản lực liên kết 12
R
G
từ khâu 1 sang khâu 2 ( 12
R
G
đi qua A);
+ Phản lực liên kết 04
R
G
từ giá sang khâu 4 ( 04
R
G
đi qua D);
+ Phản lực liên kết 05
R
G
từ giá sang khâu 5 ( 05
R
G
⊥yy).
Hình 1.1.
• Phân tích t
04
n
0404 RRR
G
G
G
+= ( n
04
R
G
nằm dọc DC, t
04
R
G
⊥DC). Tưởng tượng tách riêng khâu 4
và lập phương trình cân bằng mômen của hệ lực trên khâu 4 đối với điểm C, ta được:
0. 4CD04 =− MlRt ⇒ 21000
2
2000
CD
4
04 === l
M
Rt(N)
Chiều thực của t
04
R
G
cũng là chiều giả thiết trên hình vẽ.
• Tưởng tượng tách riêng khâu 2 và lập phương trình cân bằng lực của riêng khâu 2,
0
3212
G
G
G
=+ RR ( 32
R
G
⊥Ck, không vẽ trên hình) rồi suy ra 3212 RR
G
G
−= . Do 32
R
G
⊥EC nên 12
R
G
⊥EC.
Kết quả, 12
R
G
đi qua A và vuông góc với Ck.
• Tưởng tượng tách riêng khâu 5 và đặt phản lực liên kết 45
R
G
từ khâu 4 sang khâu 5, 45
R
G
đi qua E. Từ phương trình cân bằng mômen của hệ lực trên khâu 5 đối với tâm E, ta suy ra
05
R
G
cũng đi qua E. Kết quả, 05
R
G
đi qua E và vuông góc với yy.
• Đến đây, đường tác dụng của các lực n
04
R
G
, 12
R
G
, 05
R
G
đã được xác định. Lập phương trình
cân bằng mômen của hệ lực tác dụng trên cả nhóm Axua đối với điểm Axua S (chú ý những
kết quả đã nhận được ở trên), ta được:
02.22.2. 54043212 =+−+−−− aPMaRaPMaR t
Suy ra:
4
)2.22.(
2
1
54043212 aPMaRaPM
a
Rt+−+−−=
22000)2.3000200022.210001.20002000(
2
1
12 =+−+−−=R(N)
RA=R12=22000 N
• Phương trình cân bằng lực của cả nhóm Axua:
0
055312
t
04
n
04
G
G
G
G
G
G
G
=+++++ RPPRRR
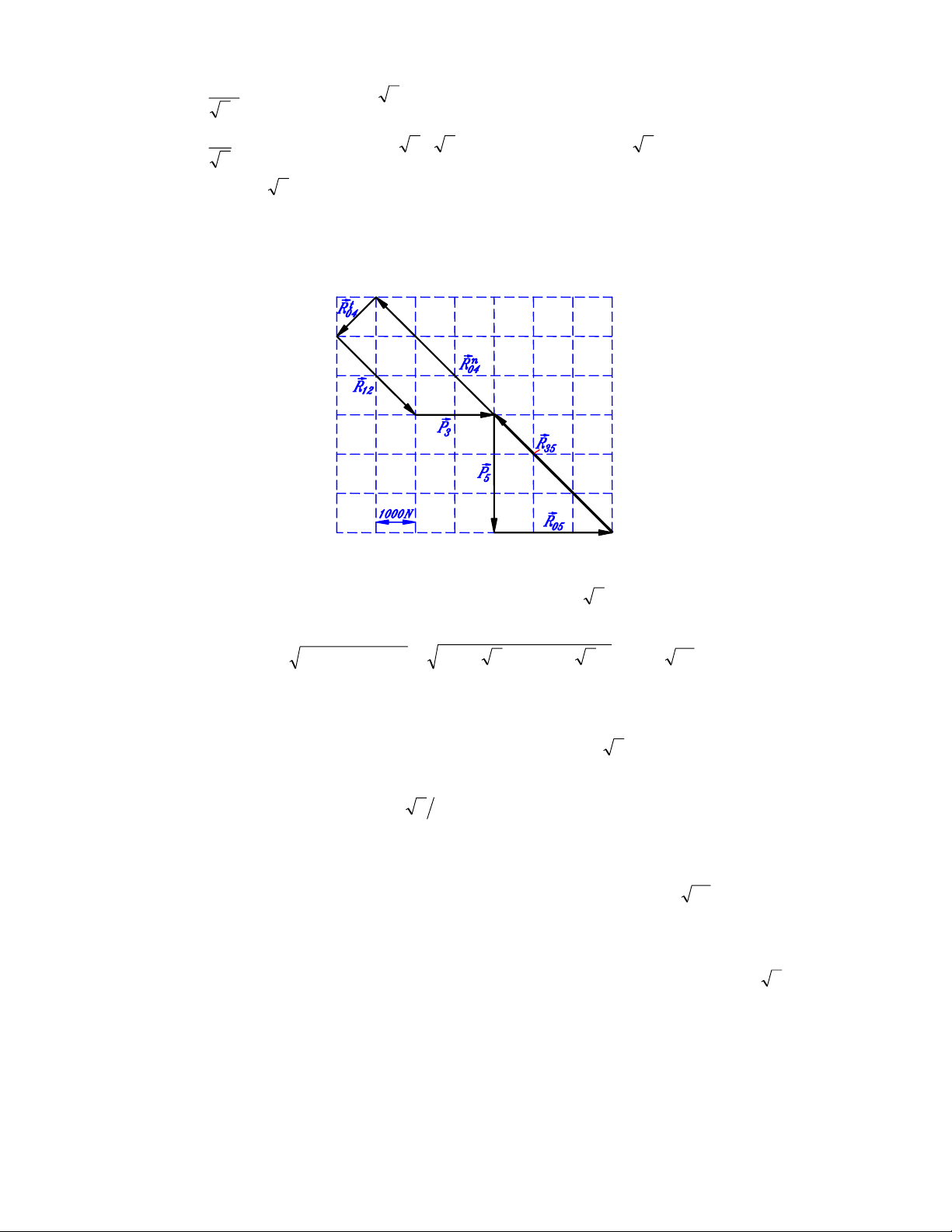
cho phép vẽ họa đồ lực như trên hình 1.2.
Hình 1.2.
Từ họa đồ lực hình 1.2, ta tìm được: 3000
05
=
RN, 26000
04 =
n
RN.
Suy ra trị số phản lực liên kết tại khớp quay D và khớp tịnh tiến E:
RD = R04 = 741000)21000()26000()()( 222
04
2n
04 =+=+ t
RR (N),
RE(T) = R05 = 3000N.
• Phương trình cân bằng lực của riêng khâu 2, 0
3212
G
G
G
=+ RR , cho 1232 RR
G
G
−= . Theo đó, trị
số phản lực liên kết tại khớp tịnh tiến B là: RB=R32=R12=22000 N. Phương trình cân bằng
mômen của hệ lực trên khâu 2 đối với điểm A cho phép suy ra cánh tay đòn của 32
R
G
nằm
cách điểm A một khoảng h=M2/R32=22 (m) về phía bên trên (đường tác dụng của 32
R
G
đi
qua điểm H trên hình 1.1).
• Phương trình cân bằng lực của riêng khâu 4, 0
0434
G
G
G
=+ RR , cho 0434 RR
G
G
−= . Theo đó,
phản lực liên kết tại khớp quay C đi qua C và có trị số: RC=R34=R04=741000 N.
• Phương trình cân bằng lực của riêng khâu 5, 0
04535
G
G
G
G
=++ RPR , chứng tỏ vectơ 35
R
G
khép kín đa giác lực của khâu 5. Bằng cách biểu diễn phương trình này lên họa đồ lực hình
1.2, ta suy ra phản lực liên kết tại khớp quay E đi qua tâm E và có trị số: RE(Q)=23000 N.
b) Xét cân bằng của khâu dẫn 1 (hình 1.3). Hệ lực tác dụng trên khâu 1 gồm:
+ Phản lực 21
R
G
từ khâu 1 ( 1221 RR
G
G
−= , đi qua A và tạo góc 450 với phương nằm ngang).
+ Phản lực liên kết 01
R
G từ gíá ( 01
R
G
đi qua O).
+ Mômen M1 trong vai trò mômen cân bằng (giả thiết M1 cùng chiều kim đồng hồ).
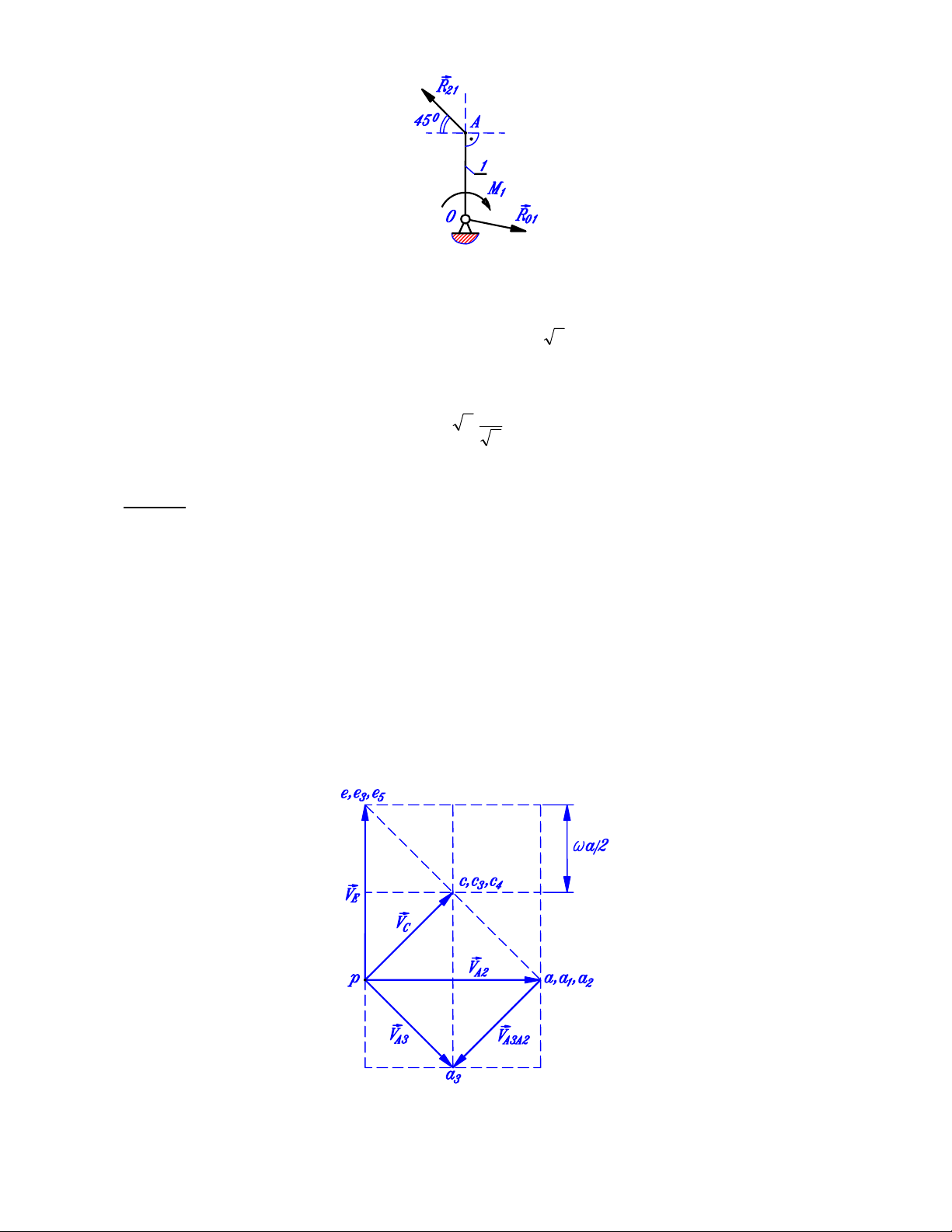
5
Hình 1.3.
• Phương trình cân bằng lực của khâu 1 ( 0
2101
G
G
G
=+ RR ) cho ta 122101 RRR
GG
G
=−= . Theo đó,
phản lực liên kết tại khớp O có trị số: RO=R01=R12=22000 N.
Phương trình cân bằng mômen của khâu 1 đối với điểm O cho phép tìm giá trị của
mômen M1 trong vai trò mômen cân bằng:
20001.
2
1
.22000.45cos OA
0
21cb1 ==== lRMM (Nm)
Vậy, mômen M1 cùng chiều kim đồng hồ và có giá bằng 2000Nm.
Câu 2.2: [5.0 điểm]
Chúng ta sẽ giải bài toán bằng cách áp dụng điều kiện cân bằng công suất.
• Trước hết, cho khâu 1 một vận tốc góc có giá trị ω1=ω (rad/s), cùng chiều kim đồng hồ
rồi vẽ họa đồ vận tốc nhằm xác định vận tốc dài của các điểm đặt lực và vận tốc góc của các
khâu mà trên đó đặt mômen. Họa đồ được vẽ như trên hình 1.4 nhờ sử dụng điểm Axua S có
vị trí như biểu diễn trên hình 1.2 (S cũng là tâm vận tốc tức thời tuyệt đối của khâu 3) và
phương trình quan hệ vận tốc của các trùng điểm A1, A2, A3:
2A3A2A3A VVV
G
G
G
+= ( 1A2A VV
G
G
=)
⊥AS ⊥OA //EC
ω3.lAS ω1.lOA -----
(?) ωa (?)
Hình 1.4.