Câu 1. Các d ng c u t o c a h p kim .ạ ấ ạ ủ ợ
C u t o c a hk tùy thu c vào l ng tác d ng t ng h c a các nguyên t trong đó. tr ngấ ạ ủ ộ ượ ụ ươ ỗ ủ ố ở Ở ạ
thái r n, HK s có các d ng c u t o sau:ắ ẽ ạ ấ ạ
− Dung d ch r n.ị ắ
− Các pha trung gian.
− H n h p c h c.ỗ ợ ơ ọ
Dung d ch r n ị ắ là m t pha tinh th , trong đó nguyên t c a nguyên t th nh t (A) gi nguyênộ ể ử ủ ố ứ ấ ữ
ki u m ng; trong khi nguyên t c a NT th 2 (B) chèn vào m ng c a A. ể ạ ử ủ ứ ạ ủ
Nguyên t nhi u h n đ c g i là dung môi. Nguyên t ít h n đ c g i là ch t tan.ố ề ơ ượ ọ ố ơ ượ ọ ấ
Vì v y m ng c a dd r n là m ng c a dung môi.ậ ạ ủ ắ ạ ủ
Tùy thu c vào cách chèn c a ch t tan vào m ng c a dung môi mà ta có 2 lo i dd r n là dd r n thay thộ ủ ấ ạ ủ ạ ắ ắ ế
và dd r n xen k .ắ ẽ
Dung d ch r n thay thị ắ ế là dd r n mà các nguyên t ch t tan thay vào v trí nút m ng c a dungắ ử ấ ị ạ ủ
môi. Tùy thu c vào kh năng thay th mà ta có 2 lo i dd r n thay th :ộ ả ế ạ ắ ế
+ dd r n thay th hòa tan vô h n là dd r n mà % ch t tan tăng t 0 đ n 100%ắ ế ạ ắ ấ ừ ế
+ dd r n thay th hòa tan có h n là dd r n mà thành ph n ch t tan b gi i h n 1 hàm l ng nh tắ ế ạ ắ ầ ấ ị ớ ạ ở ượ ấ
đ nh.ị
Đi u ki n t o thành dung d ch r n thay th :ề ệ ạ ị ắ ế
− S t ng quan v ki u m ng : 2 NT có cùng ki u m ng thì có th hòa tan vô h n, ng c l i thì chự ươ ề ể ạ ể ạ ể ạ ượ ạ ỉ
có th hòa tan có h n.ể ạ
− T ng quan v bán kính nguyên t : n u đkính gi a dmôi và chtan sai khác l n có th gây ra tr ngươ ề ử ế ữ ớ ể ườ
s đàn h i l n, d n đ n không t n t i đ c ki u m ng hòa tan. Trong th c t , n u Δd>15% thì cóư ồ ớ ẫ ế ồ ạ ượ ể ạ ự ế ế
th hòa tan có h n.ể ạ
− Tr s n ng đ đi n t : là s đi n t hóa tr tính cho 1 nguyên t . Khi t o thành dd r n thay th thìị ố ồ ộ ệ ử ố ệ ử ị ử ạ ắ ế
tr s n ng đ đi n t ph i < 1 giá tr xác đ nh tùy thu c vào bán kính nguyên t và đ c đi m c aị ố ồ ộ ệ ử ả ị ị ộ ử ặ ể ủ
dmôi.
− Các tính ch t lí hóa g n gi ng nhau.ấ ầ ố
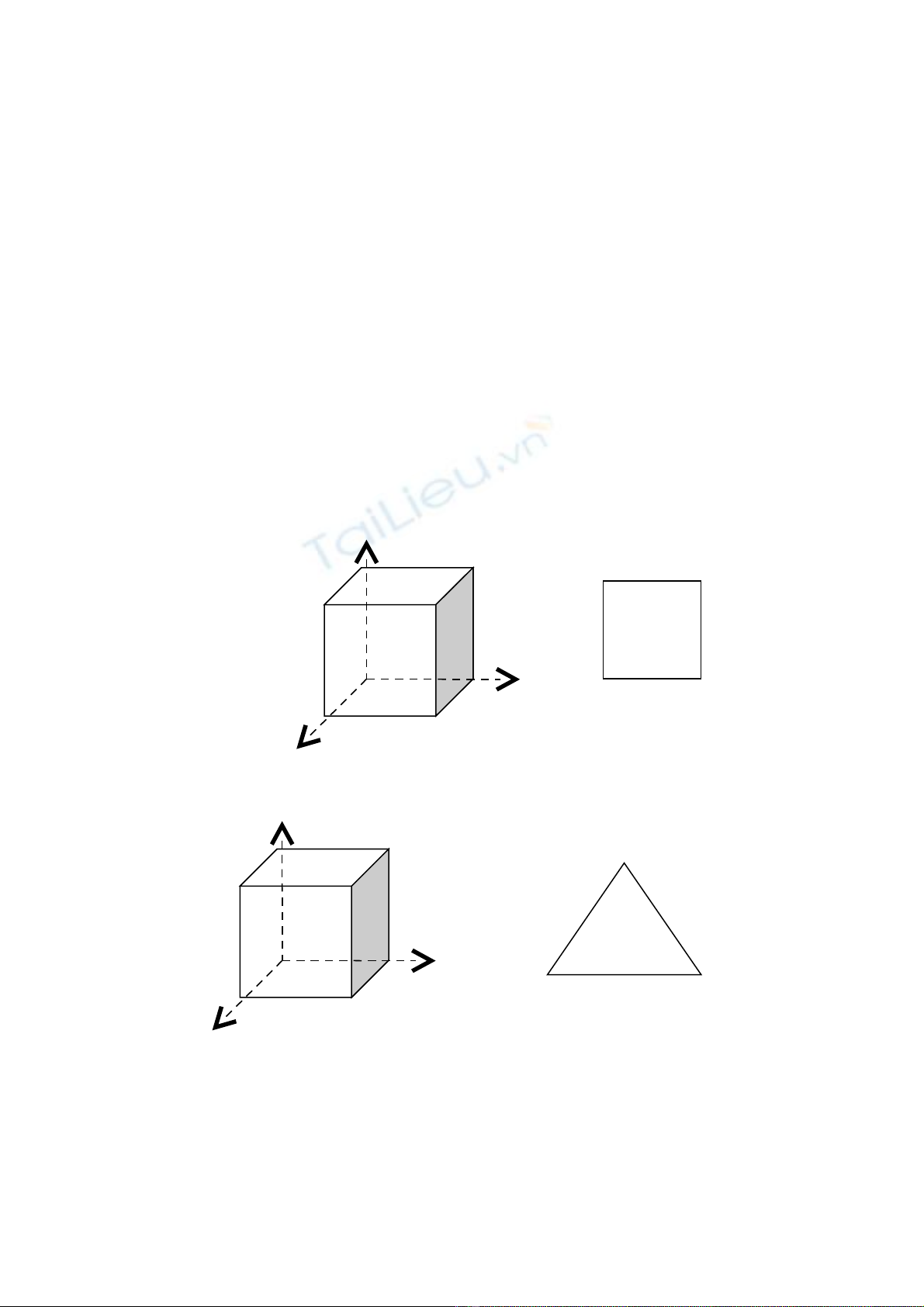
(hình 1- dd r n thay th ) ắ ế
Dung d ch r n xen kị ắ ẽ là dd r n mà nguyên t ch t tan chen vào l h ng trong m ng c a dmôi.ắ ử ấ ỗ ổ ạ ủ
Đi u ki n t o thành dd r n xen k : ề ệ ạ ắ ẽ
Đ ng kính ch t tan ≤ đ ng kính l h ng c a dmôi.ườ ấ ườ ỗ ổ ủ
Trong th c t : dự ế ct /ddm ≤ 0,59 là có th t o đ c dd r n xen k .ể ạ ượ ắ ẽ
Các ch t tan th ng là các á kim (C,B,O,N,Be..)ấ ườ
( hình v - dd r n xen k )ẽ ắ ẽ
Đ c đi m c a dd r n :ặ ể ủ ắ
− Có tính kim lo iạ
− Thành ph n dd r n bi n đ i trong ph m vi r ng.ầ ắ ế ổ ạ ộ
− M ng c a dd r n chính là m ng c a dmôi.ạ ủ ắ ạ ủ
− M ng c a dd r n luôn luôn b xô l ch.ạ ủ ắ ị ệ
Các pha trung gian : Ngoài t ng tác hòa tan, các nguyên t c a các nguyên t có th tác d ngươ ử ủ ố ể ụ
v i nhau đ t o thành m t pha khác dd r n đ c g i chung là pha trung gian. ớ ể ạ ộ ắ ượ ọ
M ng tinh th c a các pha trung gian khác v i m ng c a các nguyên t o thành nó. ạ ể ủ ớ ạ ủ ạ
D a vào đ c đi m liên k t và c u trúc m ng ng i ta chia thành các pha khác nhau : ự ặ ể ế ấ ạ ườ
− H p ch t hóa h c hóa tr th ng.ợ ấ ọ ị ườ
− Pha Laves.
1
− Pha σ
− Pha đi n tệ ử
− Pha xen kẽ
H n h p c h c là HK r n g m dd r n và các pha trung gian. Trong dd r n th ng g m nhi u pha.ỗ ợ ơ ọ ắ ồ ắ ắ ườ ồ ề
N u nh các pha n m riêng r theo 1 quy lu t, c u t o nh v y đgl h n h p c h c bình th ng.ế ư ằ ẽ ậ ấ ạ ư ậ ỗ ợ ơ ọ ườ
vd : có 2 pha : A+B
N u nh các pha n m d i d ng các t m, h t chen l n đ u nhau thì t ch c t o thành :ế ư ằ ướ ạ ấ ạ ẫ ề ổ ứ ạ
+ đgl h n h p c h c cùng tinh (hay t ch c cùng tinh) n u chúng đ c sinh ra t tr ng thái l ng. vdỗ ợ ơ ọ ổ ứ ế ượ ừ ạ ỏ
có 2 pha A,B thì t ch c cùng tinh kí hi u là : (A+B)ổ ứ ệ
+ đgl h n h p c h c cùng tích (hay t ch c cùng tích) n u chúng đ c sinh ra t tr ng thái r n. vd cóỗ ợ ơ ọ ổ ứ ế ượ ừ ạ ắ
2 pha A,B thì t ch c cùng tích kí hi u là : [A+B]ổ ứ ệ
Câu 2. Bi n d ng d o x y ra trong đ n tinh th :ế ạ ẻ ả ơ ể
Bi n d ng d oế ạ ẻ trong đ n tinh th đ c th c hi n d i 2 hình th c : tr t và song tinh(đ iơ ể ượ ự ệ ướ ứ ượ ố
tinh). Trong đó tr t là hình th c bi n d ng d o chính còn song tinh ch đóng góp trong quá trình bi nượ ứ ế ạ ẻ ỉ ế
d ng r t nh . Ch y u là trong các tr ng h p :ạ ấ ỏ ủ ế ườ ợ
− T c đ đ t t i tr ng đ t ng t.ố ộ ặ ả ọ ộ ộ
− Đ i v i nh ng m ng tinh th có tính đ i x ng th p.ố ớ ữ ạ ể ố ứ ấ
Tr tượ là s d ch d i gi a 2 ph n tinh th theo m t và ph ng xác đ nh đgl m t tr t và ph ngự ị ờ ữ ầ ể ặ ươ ị ặ ượ ươ
tr t.ượ
Các m t tr t và ph ng tr t c b n:ặ ượ ươ ượ ơ ả
− M ng l p ph ng th tâm : ạ ậ ươ ể
m t x p ch t ( tr t ) (110) −> h m t {110}ặ ế ặ ượ ọ ặ
h tr t : 6 m t x 2 ph ng = 12 cách tr t .ệ ượ ặ ươ ượ
− M ng l p ph ng di n tâm :ạ ậ ươ ệ
+ m t tr t (111) => h m t {111}ặ ượ ọ ặ
+ ph ng tr t [110]ươ ượ
+ h tr t : 4 m t x 3 ph ng = 12 cách tr t.ệ ượ ặ ươ ượ
− Là h d tr t nh tệ ễ ượ ấ
− M ng l c ph ng x p ch tạ ụ ươ ế ặ
h tr t : 1 m t x 3 ph ng = 3 cách.ệ ượ ặ ươ
C ch quá trình tr tơ ế ượ
s pháp k gây ra bi n d ng d o, ch có s ti p m i gây ra bi n d ng d o.Ư ế ạ ẻ ỉ ư ế ớ ế ạ ẻ
2
− D i tác d ng c a s ti p τ> τướ ụ ủ ư ế th các nguyên t n m v 2 phía c a 1 m t tr t đ ng th i đ t m iử ằ ề ủ ặ ượ ồ ờ ứ ố
liên k t và d ch đi m t s nguyên l n h ng s m ng sau đó l p l i cân b ng t i v trí m i, k t qu làế ị ộ ố ầ ằ ố ạ ậ ạ ằ ạ ị ớ ế ả
trên b m t b l i 1 b c c p m i, t c đã x y ra bi n d ng d o.ề ặ ỏ ạ ậ ấ ớ ứ ả ế ạ ẻ
(hình v )ẽ
Di n bi n quá trình tr t: ễ ế ượ
Đ u tiên τ> τầth : s tr t x y ra trên nh ng m t tr t c b n nh ng đ nh h ng phù h p v i t iự ượ ả ữ ặ ượ ơ ả ư ị ướ ợ ớ ả
tr ng, t o thành nh ng đ ng tr t m nh, song song đgl tr t t vi.ọ ạ ữ ườ ượ ả ượ ế
(hình v )ẽ
Sau đó xu t hi n các đ ng tr t thô h n là k t qu c a s tr t hàng nghìn thông s m ng, t oấ ệ ườ ượ ơ ế ả ủ ự ượ ố ạ ạ
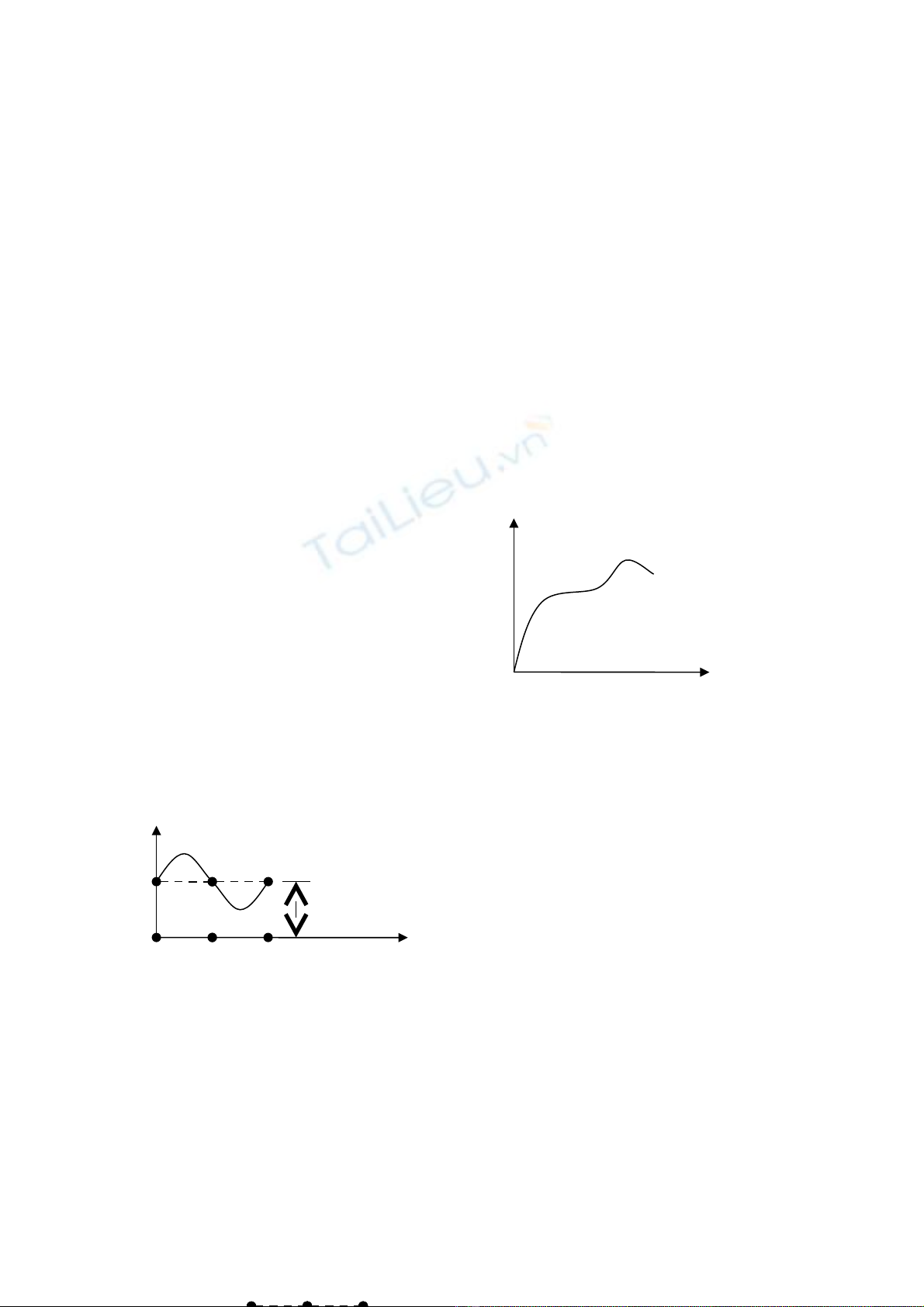
thành d i tr t. Giai đo n này tr t r t d , t ng ng v i đo n AB trên bi u đ kéo.ả ượ ạ ượ ấ ễ ươ ứ ớ ạ ể ồ
( hình v ) ẽ(hình v )ẽ
Trong quá trình tr t còn có quá trình quay c a các ph n tinh th , xu h ng sao cho m t tr t vàượ ủ ầ ể ướ ặ ượ
ph ng tr t quay v phía đ t t i tr ng; k t qu là xu t hi n các đ ng tr t m i c t các đ ngươ ượ ề ặ ả ọ ế ả ấ ệ ườ ượ ớ ắ ườ
tr t ban đ u. Giai đo n này đgl tr t khó – là đo n BC trên bi u đ .ượ ầ ạ ượ ạ ể ồ
Đ b n lý thuy t và th c t :ộ ề ế ự ế
τ = ksin(2πx/b) , 0 ≤ x ≤ b .
τmax = k = τ (b/4)
mà : τ = γG = G.x/a
=> τ = ksin(2πx/b) = G.x/a
=> k = τmax = G/2π. b/a
N u coi a≈b => ếτmax = G/2π : đây là đ b n lý thuy t. Trên th c t đ b n << G/2π vìộ ề ế ự ế ộ ề
trong kim lo i luôn ch a l ch.ạ ứ ệ
C ch tr t có l ch : Trong kim lo i th c t luôn luôn ch a l ch, d i tác d ng c a s l ch sơ ế ượ ệ ạ ự ế ứ ệ ướ ụ ủ ư ệ ẽ
chuy n đ ng, khi thoát ra ngoài b m t tinh th đ l i b c c p , đó là bi n d ng d .ể ộ ề ặ ể ể ạ ậ ấ ế ạ ư
(hình v )ẽ
Nh n xét : ậ
3
A
B
C
D
O
− D i tác d ng c a s, t i m t th i đi m ch có 1 h n ch s nguyên t xung quanh đ ng l chướ ụ ủ ư ạ ộ ờ ể ỉ ạ ế ố ử ườ ệ
tham gia vào quá trình tr t.ượ
− S có m t c a l ch t o nên m t tr ng s đàn h i xung quanh đ ng l ch. Các nguyên t xungự ặ ủ ệ ạ ộ ườ ư ồ ườ ệ ử
quanh đ ng l ch có năng l ng cao, d i tác d ng c a s l ch s chuy n đ ng theo c ch nhườ ệ ượ ướ ụ ủ ư ệ ẽ ể ộ ơ ế ư
ch y ti p s c; các nguyên t d ch chuy n nh h n h ng s m ng nên c n s th p.ạ ế ứ ử ị ể ỏ ơ ằ ố ạ ầ ư ấ
Theo Peier-Nabaro, s th c t đ c tính theo :ư ự ế ượ
, v i ν là h s poisson.ớ ệ ố
Ngu n phát sinh l ch Frank-Read:ồ ệ
Khi τ> τth :
( hình v )ẽ
+ đ đ ng cong l ch đ t c c ti u thì s có giá tr : τể ườ ệ ạ ự ể ư ị F-R = Gb/l , b là vector Bureges
+ N u ti p t c t i tr ng , đ ng l ch b u n congế ế ụ ả ọ ườ ệ ị ố
(hình v )ẽ
+ Sau m t chu kì bi n d ng t o thành vòng l ch. Các vòng l ch này khi g p các ch ng ng i m i trộ ế ạ ạ ệ ệ ặ ướ ạ ớ ở
thành ngu n l ch ( ngu n F-R)ồ ệ ồ
Nh n xétậ:
−Sau khi khi bi n d ng d o m t đ l ch r t l nế ạ ẻ ậ ộ ệ ấ ớ
−Các ch ng ng i:ướ ạ
+ Ch g p nhau c a đ ng l chỗ ặ ủ ườ ệ
+ Biên gi i h nớ ạ
+ Các pha th II trong kim lo iứ ạ
Câu 3. Đ n tinh th và đa tinh th . Bi n d ng d o trong đa tinh th .ơ ể ể ế ạ ẻ ể
N u m t v t th có m ng th ng nh t và ph ng không đ i m i đi m trong không gian đglế ộ ậ ể ạ ố ấ ươ ổ ở ọ ể
đ n tinh thơ ể. Trong th c t đ n tinh th r t ít g p, kích th c đ n tinh th r t bé và th ng ch đ cự ế ơ ể ấ ặ ướ ơ ể ấ ườ ỉ ượ
t o ra trong phòng thí nghi m.ạ ệ
Trong th c t kim lo i g m vô s các ph n t nh đgl h t tinh th , kim lo i có c u t o g mự ế ạ ồ ố ầ ử ỏ ạ ể ạ ấ ạ ồ
vô s các ph n t nh (h t tinh th ) nh v y đgl ố ầ ử ỏ ạ ể ư ậ đa tinh thể.
Gi a các h t tinh th là biên gi i h t.ữ ạ ể ớ ạ
Đ c đi m c a đ n tinh thặ ể ủ ơ ể: có tính d h ng( theo các ph ng khác nhau thì khác nhau)ị ướ ươ
Đ c đi m c a đa tinh thặ ể ủ ể : có tính đ ng h ng gi ( các ph ng khác nhau thì gi ng nhau).ẳ ướ ả ươ ố
Vùng biên gi i gi a các h t, các nguyên t s p x p h n lo n.ớ ứ ạ ử ắ ế ỗ ạ
(hình v )ẽ
Bi n d ng d o trong đa tinh th :ế ạ ẻ ể
Là t p h p t t c các bi n d ng trong đ n tinh th , nghĩa là có bi n d ng d o g m tr t và songậ ợ ấ ả ế ạ ơ ể ế ạ ẻ ồ ượ
tinh. Nh ng do các h t đ nh h ng ng u nhiên nên bi n d ng d o trong đa tinh th ph c t p h nư ạ ị ướ ẫ ế ạ ẻ ể ứ ạ ơ
nhi u. ề
Đ c đi m:ặ ể
− Do các h t đ nh h ng ng u nhiên nên h t nào mà đ nh h ng thu n l i thì bi n d ng và s nhạ ị ướ ẫ ạ ị ướ ậ ợ ế ạ ư ỏ
h n, h t nào mà đ nh h ng kém thu n l i thì bi n d ng và s l n h n.ơ ạ ị ướ ậ ợ ế ạ ư ớ ơ
− Biên gi i h t là 1 ch ng ng i kiên c , ch ng l i s chuy n đ ng c a l ch.ớ ạ ướ ạ ố ố ạ ự ể ộ ủ ệ
4
− Ta có bi u th c tính s : σể ứ ư ch = σ0 + k.d-½ . Đi u đó gi i thích t i sao KL càng m n thì có c tính càngề ả ạ ị ơ
cao.
− Bi n d ng d o trong đa tinh th có tính đ ng h ng gi .ế ạ ẻ ể ẳ ướ ả
5