TR NG THPT NGÔ GIA TƯỜ Ự
T : TOÁN TINỔ
Đ KI M TRA 45 PHÚT CH NG 1 GI I TÍCH 12Ề Ể ƯƠ Ả
NĂM H C: 2016 – 2017 (Hình th c: Ọ ứ Tr c nghi mắ ệ )
H , tên thí sinh:................................................S báo danh: ọ ố
................L p: .......... ớMã đ thiề
132
Phi u tr l i tr c nghi m: ế ả ờ ắ ệ H c sinh vi t đáp án đúng (A, B, C, D) vào phi u tr l i tr c nghi m ọ ế ế ả ờ ắ ệ
d i đâyướ
Đi mểCâu1 2 3 4 5 6 7 8 9 10 11 12 13
Đáp án
Câu14 15 16 17 18 19 20 21 22 23 24 25
Đáp án
Ph n câu h i tr c nghi mầ ỏ ắ ệ
Câu 1: Ph ng trình ti p tuy n c a đ th hàm s ươ ế ế ủ ồ ị ố
3
1y x= +
t i đi m có hoành đ ạ ể ộ
1x=
là
A.
3y x
=
.B.
3 5y x
= − +
.C.
1y x
= +
.D.
3 1y x
= −
.
Câu 2: Ti m c n đng và ti m c n ngang c a đ th hàm s ệ ậ ứ ệ ậ ủ ồ ị ố
1
2 1
x
yx
+
=+
l n l t có ph ng trình làầ ượ ươ
A.
1 1
,
2 2
x y
= =
.B.
1 1
,
2 2
x y= − =
.C.
1 1
,
2 2
x y= = −
.D.
1 1
,
2 2
x y= − = −
.
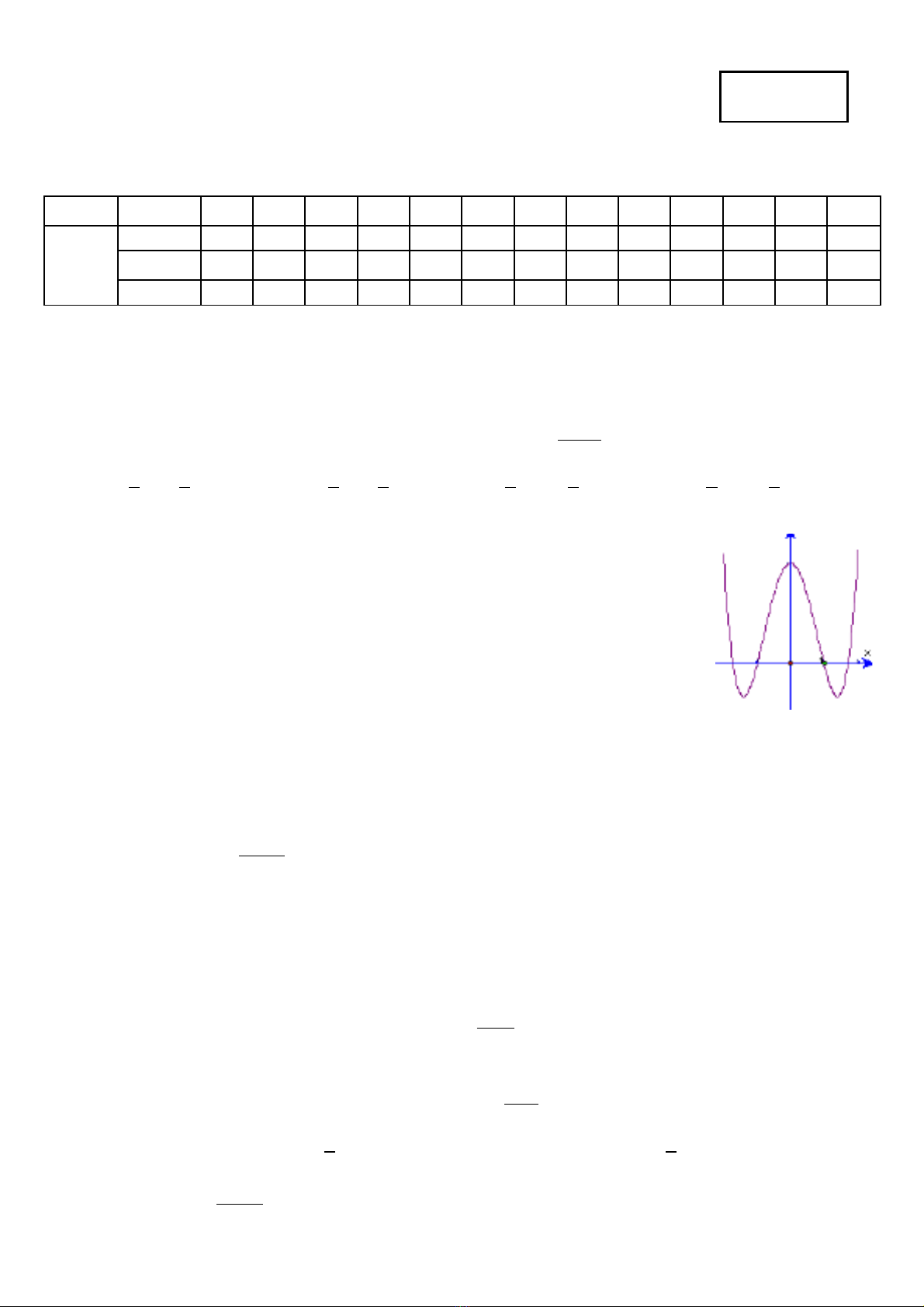
Câu 3: Đ th nh trong hình v là đ th c a hàm s nào trong các hàm s sauồ ị ư ẽ ồ ị ủ ố ố
A.
4 2
4 3y x x= − +
. B.
3
3 1y x x
=−+
. C.
4 2
2 1y x x= + +
. D.
4 2
4 3y x x
= − + −
.
Câu 4: Ch n kh ng đnh đúng.ọ ẳ ị
A.
( )y f x=
ngh ch bi n trên ị ế K
'( ) 0f x >�
v i m i ớ ọ
x K
.
B.
'( ) 0f x >
v i m i ớ ọ
x K
� �
( )y f x=
ngh ch bi n trên ị ế K.
C.
( )y f x=
ngh ch bi n trên ị ế K
'( ) 0f x =�
v i m i ớ ọ
x K
.
D.
'( ) 0f x <
v i m i ớ ọ
( )x K y f x=� �
ngh ch bi n trên ị ế K.
Câu 5: Phát bi u nào sau đây đúngể ?
A. Hàm s ố
( )y f x=
đt c c tr t i ạ ự ị ạ
0
x
thì
0
'( ) 0f x <
.
B. Hàm s ố
( )y f x=
đt c c tr t i ạ ự ị ạ
0
x
thì
0
'( ) 0f x >
.
C. Hàm s ố
( )y f x=
đt c c tr t i ạ ự ị ạ
0
x
và có đo hàm t i ạ ạ
0
x
thì
0
'( ) 0f x =
.
D. Hàm s ố
( )y f x=
đt c c tr t i ạ ự ị ạ
0
x
thì
0
'( ) 2017f x =
.
Câu 6: Cho hàm s ố
2 3
2
x
yx
+
=−
. Ch n kh ng đnh đúng.ọ ẳ ị
A. Hàm s ngh ch bi n trên ố ị ế
{ }
\ 2ᄀ
. B. Hàm s đng bi n trên ố ồ ế
(2; )
+
.
C. Hàm s đng bi n trên các kho ng ố ồ ế ả
( ;2)
−
và
( 2; )
− +
.D. Hàm s đng bi n trên ố ồ ế
{ }
\ 2ᄀ
.
Câu 7: Xác đnh m đ hàm s ị ể ố
3 2
1y x mx x= − + +
đt c c tr t i ạ ự ị ạ
1x=
?
A.
2m
= −
.B.
1m
=
.C.
2m
=
.D.
1m
= −
.
Câu 8: Ph ng trình ti p tuy n c a đ th hàm s ươ ế ế ủ ồ ị ố
3
2
x
yx
+
=+
t i đi m M(-1;2) làạ ể
A.
2y x
= −
.B.
3y x
= +
.C.
2 4y x
= +
.D.
1y x
= − +
.
Câu 9: Giá tr nh nh t và giá tr l n nh t c a hàm s ị ỏ ấ ị ớ ấ ủ ố
4
1
yx
=+
trên đo n [1;2] l n l t làạ ầ ượ
A. 1 và 5. B. 2 và
4
3
.C. 2 và 5. D.
4
3
và 2.
Câu 10: Hàm s ố
1mx
yx m
+
=+
đng bi n trên t ng kho ng xác đnhồ ế ừ ả ị khi ?
A.
1m
−
ho c ặ
1m
.B.
1m
<
.C.
1 1m
− < <
.D.
1m
< −
ho c ặ
1m
>
.
Trang 1/3 - Mã đ thi 132ề
Câu 11: Giá tr l n nh t c a hàm s ị ớ ấ ủ ố
3 2
2 3 1y x x= − +
trên đo n [0;2] làạ
A. 3. B. 5. C. 0. D. 7.
Câu 12: Cho hàm số
( )y f x=
ch có 2 gi i h n vô c c làỉ ớ ạ ự
2 5
lim , lim
x x
y y
+ −
= − = +
. Ch n kh ng đnh đúng.ọ ẳ ị
A. Đ th hàm s không có ti m c n đng.ồ ị ố ệ ậ ứ B. Đ th hàm s không có ti m c n ngang.ồ ị ố ệ ậ
C. Đ th hàm s có ti m c n đng là các đng th ng ồ ị ố ệ ậ ứ ườ ẳ
2y=
và
5y=
.
D. Đ th hàm s có ti m c n đng là các đng th ng ồ ị ố ệ ậ ứ ườ ẳ
2x
=
và
5x
=
.
Câu 13: Cho 2 đ thồ ị
( ) : ( )C y f x=
và
( ') : ( )C y g x=
. G i ph ng trìnhọ ươ
( ) ( )f x g x=
là (*). Ch n kh ng đnhọ ẳ ị
sai.
A. (*) vô nghi m thì (C) và (C’) có vô s đi m chung.ệ ố ể
B. (*) có 1 nghi m thì (C) và (C’) có 1 giao đi m. ệ ể C. (C) và (C’) có 1 giao đi m thì (*) có 1 nghi m.ể ệ
D. (*) có 2 nghi m phân bi t thì (C) và (C’) có 2 giao đi m phân bi t.ệ ệ ể ệ
Câu 14: Xác đnh ịm đ ph ng trình ể ươ
3 2 2
3 2x x m m
+ + = +
có 4 nghi m phân bi t.ệ ệ
A.
3 2
1 2
m
m
− < < −
< <
B.
3
2 2
m
m
>
− < <
.C.
2 3
1 1
m
m
< <
− < <
.D.
3 1
2
m
m
− < <
>
.
Câu 15: Hàm s ố
3 2
3 2y x x= − + −
đt c c đi, c c ti u l n l t t iạ ự ạ ự ể ầ ượ ạ
A.
2, 0x x
= − =
.B.
0, 2x x
= =
.C.
2, 0x x
= =
.D.
0, 2x x
= = −
.
Câu 16: Hàm s ố
3
2
3 12
3
x
y x= − −
ngh ch bi n trên kho ng nào trong các kho ng sau ?ị ế ả ả
A.
( ;1)
−
.B.
(6; )
+
.C. (1;4). D. (1;10).
Câu 17: Cho hàm s ố
4 2
2 12y x x= − −
. Tìm kho ng ngh ch bi n c a hàm s .ả ị ế ủ ố
A.
( ; 1)
− −
và
(0;1)
. B.
( ; 1) (0;1)
− −
. C.
( ; 1)
− −
và
(1; )
+
. D.
( 1;0)
−
và
(1; )
+
.
Câu 18: Xác đnh m đ hàm s ị ể ố
3 2 2
3 ( ) 1y x x m m x= − + − +
đt c c đi t i ạ ự ạ ạ
2x
=
?
A.
0m
=
ho c ặ
1m
=
.B.
0m
=
.C.
1m
=
.D. Không có m.
Câu 19: Ch n kh ng đnh sai.ọ ẳ ị
A. N u ế
0
'( ) 0f x =
và
0
''( ) 0f x >
thì
( )y f x=
đt c c ti u t i ạ ự ể ạ
0
x
.
B. N u ế
0
'( ) 0f x =
và
0
''( ) 0f x <
thì
( )y f x=
đt c c đi t i ạ ự ạ ạ
0
x
.
C. N u ế
0
'( ) 0f x =
và
0
''( ) 0f x
thì
( )y f x=
đt c c tr t i ạ ự ị ạ
0
x
.
D. N u ế
0
'( ) 0f x =
và
0
''( ) 0f x =
thì
( )y f x=
đt c c đi t i ạ ự ạ ạ
0
x
.
Câu 20: Xác đnh m đ hàm s ị ể ố
3
2
(2 1) 1
3
x
y mx m x= − + − +
có c c đi, c c ti u ?ự ạ ự ể
A. m b t kì.ấB.
1m
>
.C.
1m
<
.D.
{ }
\ 1m
ᄀ
.
Câu 21: Cho hàm s ố
2
1
1
x
y
x
+
=−
. S ti m c n ngang c a đ th hàm s làố ệ ậ ủ ồ ị ố
A. 0. B. 1. C. 2. D. 3.
Câu 22: Xác đnh m đ đng th ng ị ể ườ ẳ
1y x
= +
và đ th hàm s ồ ị ố
2
1
x m
yx
+
=−
có 2 giao đi m phân bi t ?ể ệ
A.
2m
> −
.B.
2m
<
.C.
0m
<
.D.
0, 2m m
< −
.
Câu 23: Xác đnh m đ đng th ng ị ể ườ ẳ
2 1y x
= −
c t đ th (C):ắ ồ ị
1
2
mx
yx
−
=+
t i 2 đi m phân bi t sao choạ ể ệ
15AB =
?
A.
1
1
m
m
= −
=
.B.
5
5
m
m
=
= −
.C.
1
5
m
m
= −
= −
.D.
1
5
m
m
= −
=
.
Câu 24: Hàm s ố
4 2
1y x x
= + +
có giá tr c c ti u làị ự ể
A.
CT 3y=
.B.
CT 1y=
.C.
CT 4y=
.D.
CT 2y=
.
Trang 2/3 - Mã đ thi 132ề

Câu 25: Đ th hàm s ồ ị ố
3 2
3 1y x x= − +
c t đng th ng ắ ườ ẳ
1y=
t i các đi m có hoành đ làạ ể ộ
A. 0 và 1. B. 0 và 3. C. 1 và 3. D. 0 và 4.
-----------------------------------------------
----------- H T ----------Ế
Trang 3/3 - Mã đ thi 132ề












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



