1
ĐỀ KIỂM TRA 45 PHÚT LẦN 2 – HK2 – LỚP 10A5
I/ PHẦN TRẮC NGHIỆM:
Câu 1. Tập nghiệm của bất phương trình 2
6 0
x x
là:
A.
; 3 2;
 
. B.
3;2
.
C.
2;3
. D.
; 2 3;

.
Lời giải
Chọn C
2
6 0 2 3
x x x
.
Vậy tập nghiệm của bất phương trình là
2;3
.
Câu 2. Tập nghiệm của bất phương trình 2
2 3 0
x x
là:
A.
. B.
. C.
( ; 1) (3; )
 
. D.
( 1;3)
.
Lời giải
Chọn B
2
22 3 1 2 0,
x x x x .
Câu 3.
2
x
là một nghiệm của bất phương trình nào trong các bất phương trình sau
A. 2
4 4 0
x x
. B. 2
2 3 0
x x
.
C. 2
6 0
x x
. D. 2
36 12 1 0
x x
.
Lời giải
Chọn C
2
6 0 2 3
x x x
.
Vậy tập nghiệm của bất phương trình là
2;3
.
Câu 4. Bất phương trình 2
( 1) 0
x x
có nghiệm là:
A.
( ; 1) [1; )
x
 
. B.
[ 1;0] [1; )
x

.
C.
( ; 1] [0;1)
x

. D.
[ 1;1]
x
.
Lời giải
Chọn B
+ Nhị thức
x
có nghiệm duy nhất
0
x
.
+ Tam thức 2
1
x
có hai nghiệm phân biệt
1
và
1
.
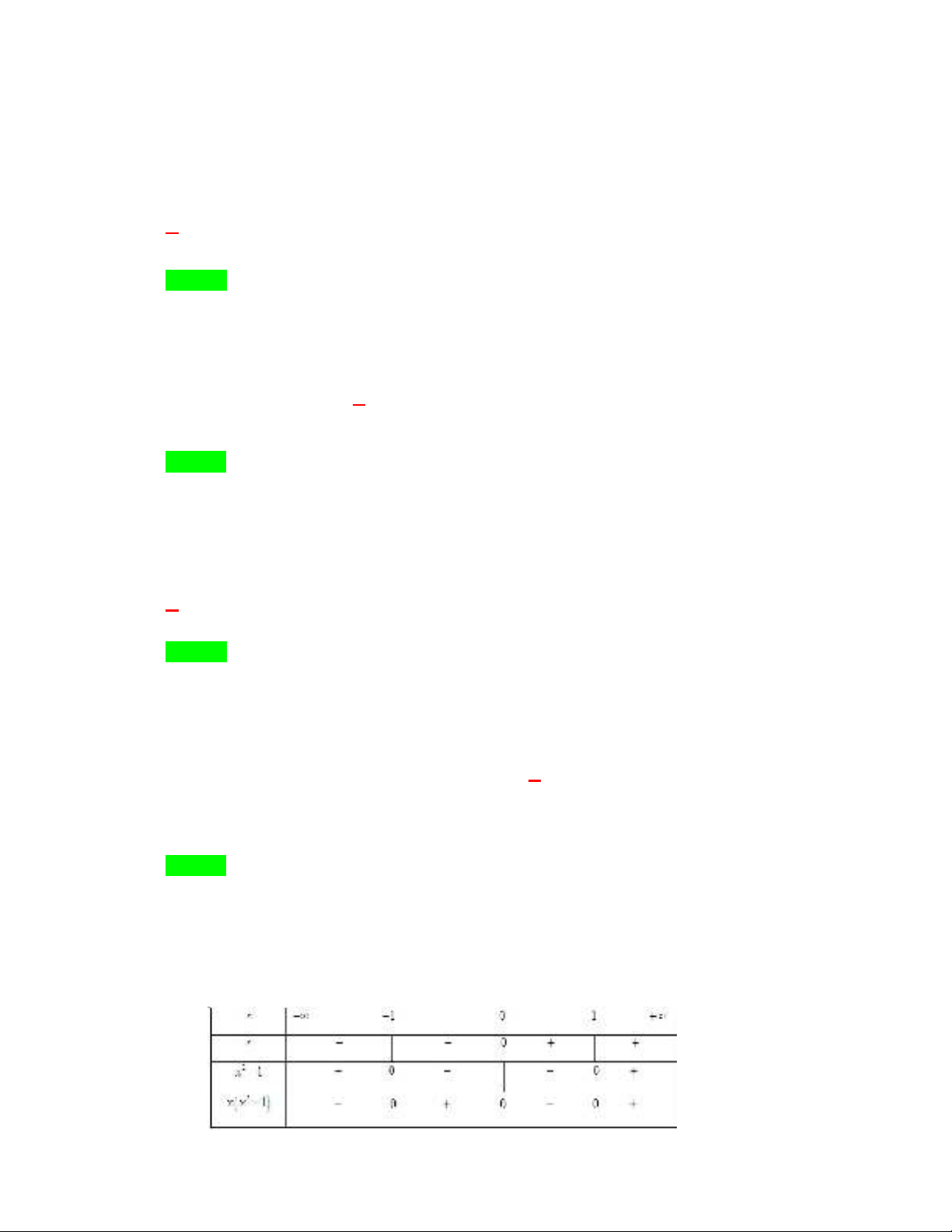
+ Ta có bảng xét dấu:
Từ bảng xét dấu ta có
2
( 1) 0 1;0 1;x x x
.
2
Câu 5. Tập nghiệm của bất phương trình: 2
5 3
0
4 4
x
x x
là
A.
3
5
x
. B.
3
5
x
và
2
x
.
C. 3
2
5
x

. D.
3
5
x
.
Lời giải
Chọn B
TXĐ:
\ 2
D
2
5 3
0
4 4
x
x x
2
5 3
0
2
x
x
3
5
2
x
x
Kết luận:
3
5
x
và
2
x
.
Câu 6. Tìm tham số
m
để phương trình 2
2 4 3 0
x mx m
có hai nghiệm phân biệt
A.
1v 3
m m
. B.
1v 3
m m
.
C.
1 3
m v m
. D.
1 3
m
.
Lời giải
Chọn B
Phương trình 2
2 4 3 0
x mx m
có hai nghiệm phân biệt
2
1
4 3 0
3
m
m m m
.
Câu 7. Tập nghiệm của bất phương trình 2
1 3
x
là:
A.
2;2
. B.
3;2
.
C.
2;3
. D.
; 2 2;
 
.
Lời giải
Chọn A
2 2
2
2 2
1 3 4 0
1 3 2 2
1 3 2 0
x x
x x
x x
.
Vậy tập nghiệm của bất phương trình là
2;2
.
Câu 8. Tập nghiệm của bất phương trình 2
3 2
x x
là:
A.
0;1
. B.
3;2
.
C.
0;2
. D.
1;0 3;4
.
Lời giải
Chọn D
2
2
2
3 0 0 v 3 1 0
3 2
1 4 3 4
3 4
x x x x x
x x x x
x x
.
3
Vậy tập nghiệm của bất phương trình là
1;0 3;4
.
Câu 9. Tập nghiệm của hệ bất phương trình
2
2
3 2 0
1 0
x x
x
là:
A.
. B.
{1}
. C.
[1;2]
. D.
[ 1;1]
.
Lời giải
Chọn B
2
2
1 2
3 2 0
1
1 1
1 0
x
x x
x
x
x
.
Câu 10. Tìm tất cả các giá trị của
m
để biểu thức
2
2 8 1
x m x m
luôn dương với mọi
x
A.
0 20
m m
. B.
0 20
m
.
C.
0 28
m m
. D.
0 28
m
.
Lời giải
Chọn D
Ta có hệ số
1 0
a
; 2
28
m m
.
22 8 1 0,x m x m x
0
2
28 0
m m
0 28
m
.
Câu 11. Một vectơ chỉ phương của đường thẳng
2 3
3
x t
y t
là:
A.
1
2; –3 .
u
B.
2
3; –1 .
u
C.
3
3; 1 .
u
D.
4
3; –3
u
Lời giải
Chọn B
Từ phương trình tham số của đường thẳng ta có một VTCP của đường thẳng là
2
3; –1 .
u
Câu 12. Một vectơ pháp tuyến của đường thẳng
2 3 6 0
x y
là :
A.
4
2; 3
n
B.
2
2;3
n
C.
3
3; 2
n
D.
1
3; 2
n
Lời giải
Chọn A
Từ PTTQ ta thấy một VTPT của đường thẳng là
4
2; 3
n
Câu 13. Cho
2 3
:
5 4
x t
d
y t
. Điểm nào sau đây không thuộc
?
d
A.
5;3 .
A B.
2;5 .
B C.
1;9 .
C D.
8; 3 .
D
Lời giải
Chọn A.
Thay
1
5 2 3
5;3
1
3 5 4
2
t
t
Att
5;3
A d
Câu 14. Viết phương trình tham số của đường thẳng đi qua
3;4
A và có vectơ chỉ phương
3; 2
u
4
A.
3 3
2 4
x t
y t
. B.
3 6
2 4
x t
y t
. C.
3 2
4 3
x t
y t
. D.
3 3
4 2
x t
y t
.
Lời giải
Chọn D
Phương trình tham số của đường thẳng đi qua
3;4
A và có vectơ chỉ phương
3; 2
u
có dạng:
3 3
4 2
x t
y t
.
Câu 15. Phương trình tổng quát của đường thẳng đi qua
1; 2
A và nhận
1; 2
n làm véc-tơ pháp tuyến
có phương trình là
A.
2 0
x y . B.
2 4 0
x y . C.
2 5 0
x y . D.
2 4 0
x y .
Lời giải
Chọn C
Phương trình đường thẳng là
1 1 2 2 0
x y hay
2 5 0
x y .
Câu 16. Phương trình đường thẳng đi qua hai điểm
2;4
A,
6;1
B là
A.
3 4 10 0
x y
. B.
3 4 22 0
x y
. C.
3 4 8 0
x y
. D.
3 4 22 0
x y
.
Lời giải
Chọn B
Ta có
4; 3
AB
.
Đường thẳng
AB
qua điểm
2;4
A và nhận
1
VTPT là
3; 4
n
nên có phương trình:
3 2 4 4 0
x y
3 4 22 0
x y
.
Câu 17. Xét vị trí tương đối của hai đường thẳng 1
:3 2 6 0
d x y
và 2
:6 2 8 0
d x y
.
A. Trùng nhau. B. Song song.
C. Vuông góc với nhau. D. Cắt nhau .
Lời giải
Chọn D
1
1 1
2
1 2
22
3
:3 2 6 0 3; 2 6
: 6 2 8 0 6; 2
0
2
2
,
d x y n
d d
nn
xn
d y
cắt nhau nhưng không vuông góc.
Câu 18. Hai đường thẳng
1
2 5
:2
x t
dy t và
2
:4 3 18 0
d x y . Cắt nhau tại điểm có tọa độ:
A.
2;3 .
B.
3;2 .
C.
1;2 .
D.
2;1 .
Lời giải
Chọn B
5
Ta có
1 1
2 5
: : 2 5 4 0
2
x t
d d x y
y t
Gọi
1 2
M d d
M
là nghiệm của hệ phương trình
2 5 4 0 3
4 3 18 0 2
x y x
x y y
Câu 19. Cho hai đường thẳng
1 2
: 1 , : 2
d mx y m d x my song song nhau khi và chỉ khi
A.
2.
m B.
1.
m C.
1.
m D.
1.
m
Lời giải
Chọn D.
1 2
;
d d
song song nhau
2
2
1
1
1
1
1
2
2
m
m
mm
m
m m
m
Câu 20. Khoảng cách từ điểm
1; 1
M
đến đường thẳng
:3 4 17 0
x y
bằng
A.
2
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn A.
Áp dụng công thức tính khoảng cách ta có
2
3
3.1 4 1 17
,
3 4
d M
10
5
2
.
II/ PHẦN TỰ LUẬN
Bài 1. Giải các bất phương trình sau:
1) 2
3 2 1 0
x x
. (0,75 điểm)
2) 2
3 2 1
x x x
.(0,75 điểm)
3) 2
2 15 4
x x x
.(1,0 điểm)
Lời giải
1) Tam thức 2
( ) 3 2 1
f x x x
có
3 0
a
và có hai nghiệm 1
1
;
3
x
2
1
x
. (0,25 điểm)
Lập bảng xét dấu (0,25 điểm)
Suy ra 21
3 2 1 0 1
3
x x x
(0,25 điểm)
Vậy tập nghiệm của bất phương trình : 1
;1
3
S
.
2) 2
3 2 1
x x x
2
2
3 2 1
3 2 1
x x x
x x x
(0,25 điểm)
2
2
2 3 0
4 1 0
x x
x x
3 1
2 5 v 2 5
x
x x
(0,25 điểm)