Đ:Ề
A.PH N CHUNG : (8 đi m)Ầ ể (dành chung cho c hai ban).ả
Câu 1. (3,0 đi m) ểTìm t p xác đnh c a các hàm s sau :ậ ị ủ ố
1.
2
cos 1
yx
=−
2.
tan 3
y x
π
� �
= +
� �
� �
Câu 2. (5,0 đi m) ểGi i các ph ng trình sau :ả ươ
1.
2sin 1 0
6
x
π
� �
+ − =
� �
� �
.
2.
2
2cos 3cos 1 0x x− + =
.
3.
2
2sin 3 sin 2 2x x+ =
I. Ph n dành riêng cho ban c b n :ầ ơ ả
Câu 3. (2,0 đi m)ể
Gi i các ph ng trình sau : ả ươ
1.
( )
sin2 . 2sin 2 0x x − =
.
2.
2
sin 2cos 2 0
3 3
x x
− + =
.
Câu 4. (2,0 đi m) ểGi i các ph ng trình sau : ả ươ
1.
2sin cos sin 2 1 0x x x
+ − − =
.
2.
2 2
7
sin .cos 4 sin 2 4sin 4 2 2
x
x x x
π
� �
− = − −
� �
� �
.
--------------------
Đ:Ề
A.PH N CHUNG : (8 đi m)Ầ ể (dành chung cho c hai ban).ả
Câu 1. (3,0 đi m) ểTìm t p xác đnh c a các hàm s sau :ậ ị ủ ố
1.
2
cos 1
yx
=−
2.
tan 3
y x
π
� �
= +
� �
� �
Câu 2. (5,0 đi m) ểGi i các ph ng trình sau :ả ươ
1.
2sin 1 0
6
x
π
� �
+ − =
� �
� �
.
2.
2
2cos 3cos 1 0x x− + =
.
3.
2
2sin 3 sin 2 2x x+ =
I. Ph n dành riêng cho ban c b n :ầ ơ ả
Câu 3. (2,0 đi m)ể
Gi i các ph ng trình sau : ả ươ
1.
( )
sin2 . 2sin 2 0x x − =
.
2.
2
sin 2cos 2 0
3 3
x x
− + =
.
Câu 4. (2,0 đi m) ểGi i các ph ng trình sau : ả ươ
1.
2sin cos sin 2 1 0x x x+ − − =
.
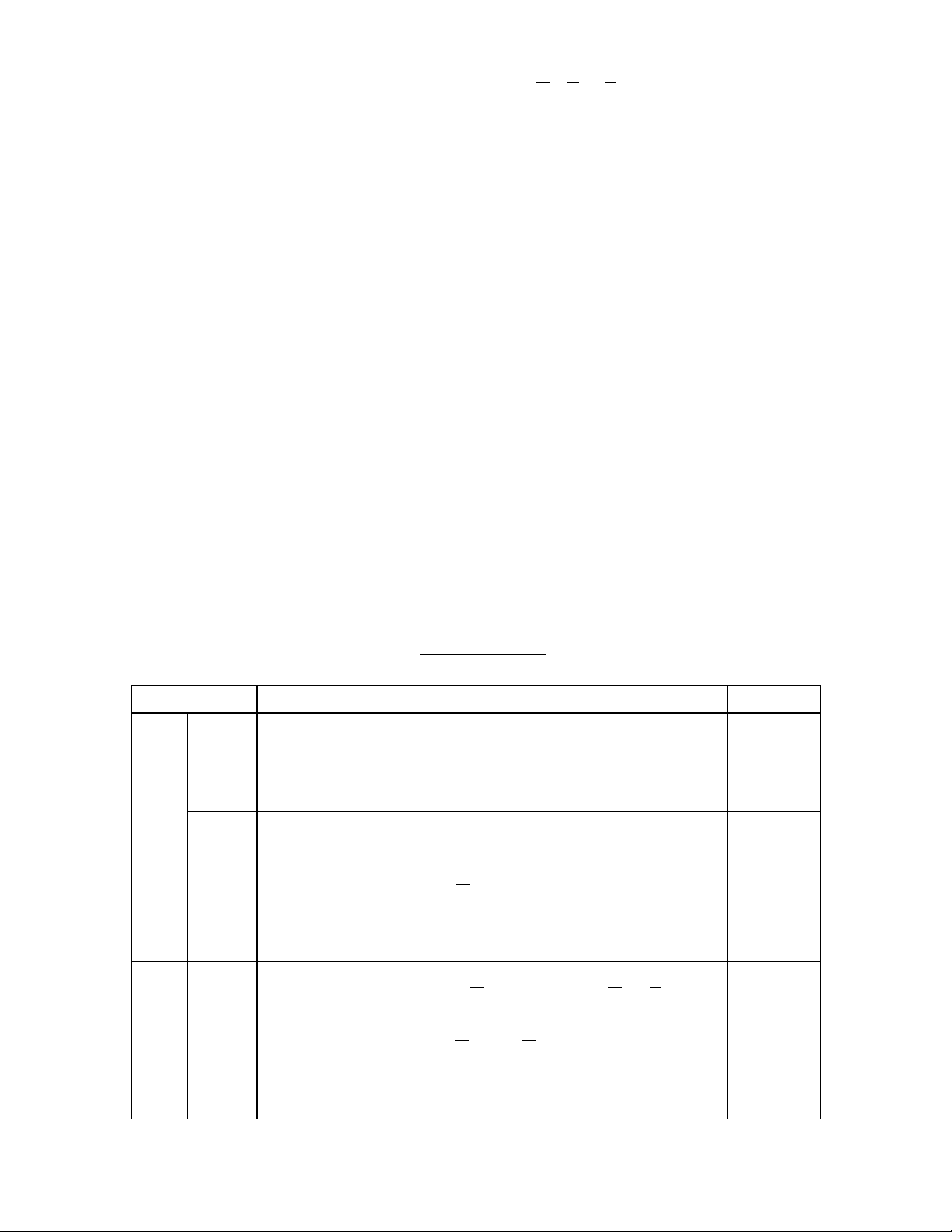
2.
2 2
7
sin .cos 4 sin 2 4sin 4 2 2
x
x x x
π
� �
− = − −
� �
� �
.
ĐÁP ÁN KI M TRA MÔN GI I TÍCH 11Ể Ả
Môn : TOÁN.
CÂU BÀI GI IẢĐI MỂ
1
(3)
1
(1,5)
Hàm s xác đnh ố ị
cos 1x
۹
2x k
π
۹
.
V y t p xác đnh c a hàm s : ậ ậ ị ủ ố
{ }
\ 2D R k
π
=
.
0,5
0,25
0,25
0,5
2
(1,5)
Hàm s xác đnh ố ị
3 2
x k
π π π
+ +� �
6
x k
ππ
+۹
V y t p xác đnh c a hàm s : ậ ậ ị ủ ố
\6
D R k
ππ
� �
= +
� �
�
.
0,5
0,5
0,5
1
(1,75)
Ph ng trình ươ
2sin 1
6
x
π
� �
+ =�� �
� �
1
sin 6 2
x
π
� �
+ =�� �
� �
sin sin
6 6
x
π π
� �
+ =�� �
� �
0,25+0,25
0,5
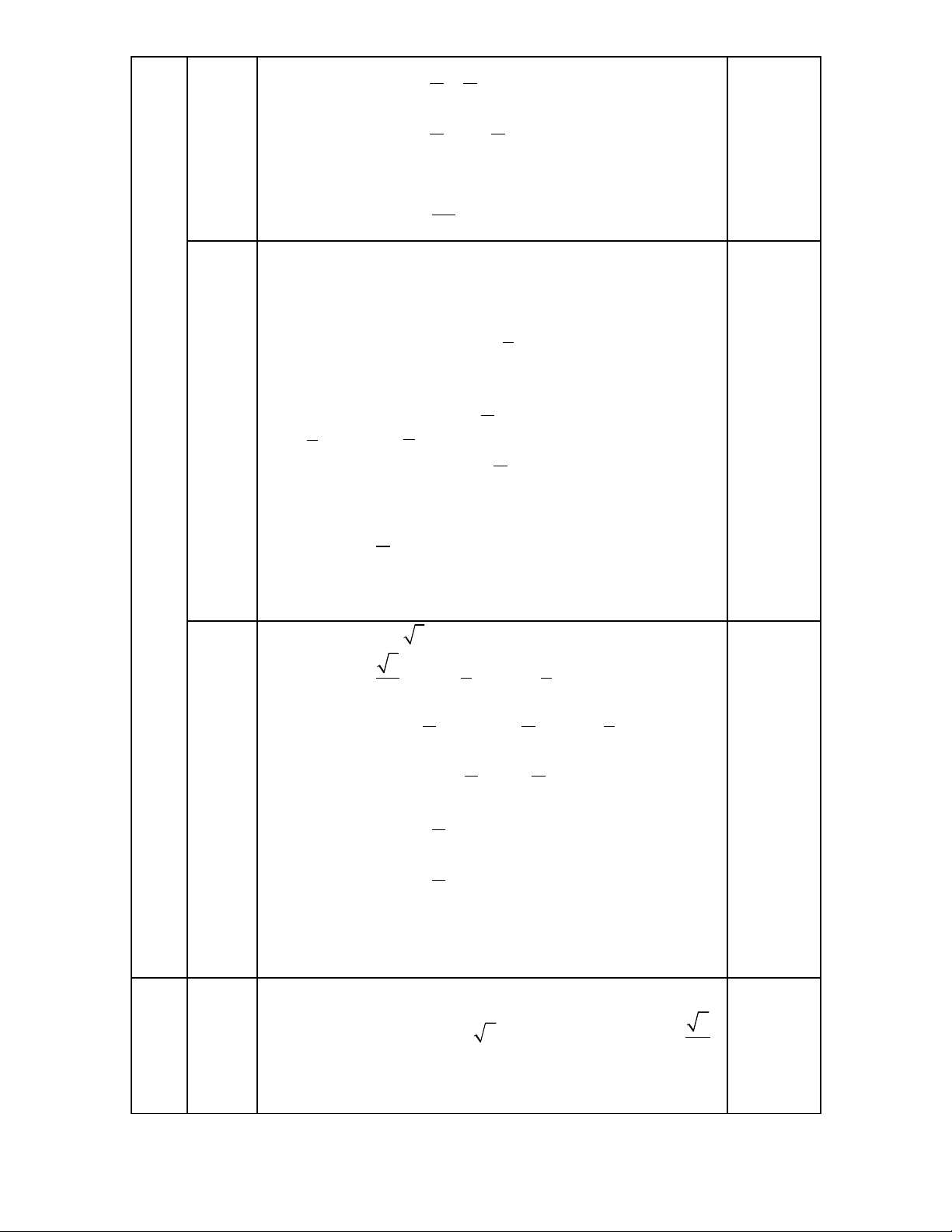
2
(5)
2
6 6
2
6 6
x k
x k
π π π
π π
π π
+ = +
+ = − +
2
22
3
x k
x k
π
ππ
=
= +
0,5
0,25
2
(1,75)
Đt : ặ
cos x t=
; đi u ki n : ề ệ
1 1t
−
.
Ph ng trình tr thành : ươ ở
2
2 3 1 0t t− + =
1
1
2
t
t
=
=
(th a đi u ki n)ỏ ề ệ
*
1t
=
:
cos 1 2x x k
π
= =�
.
*
1
2
t=
:
2
13
cos 22
3
x k
x
x k
ππ
ππ
= +
= = − +
.
V y : ậ
2
2
3
x k
x k
π
ππ
=
= +
.
(L u ý: Hs có th gi i tr c ti p, n u đúng v n cho ư ể ả ự ế ế ẫ
đi m t i đa )ể ố
0,25
0,25
0,5
0,25
0,25
0,25
3
(1,5)
Ph ng trình ươ
3 sin2 cos 2 1x x x− =�
3 1 1
sin2 cos 2
2 2 2
x x− =
1
cos sin2 sin cos 2
6 6 2
x x
π π
− =�
sin 2 sin
6 6
x
π π
� �
− =�� �
� �
6
2
x k
x k
ππ
ππ
= +
= +
(L u ý: Hs có th gi i theo d ng ph ng trình đng ư ể ả ạ ươ ẳ
c p ho c đa v pt tích, n u đúng v n cho đi m t i đa ấ ặ ư ề ế ẫ ể ố
t ng ng).ươ ứ
0,25
0,25
0,25
0,25
0,25
1
Ph ng trình ươ
sin2 0
2sin 2 0
x
x
=
− =
0,25+0,25
3
(2)
(1)
2
2
4
32
4
x k
x k
x k
π
ππ
ππ
=
= +�= +
2
2
4
32
4
x k
x k
x k
π
ππ
ππ
=
= +�= +
0,25+0,25
2
(1)
Ph ng trình ươ
2
cos 2cos 3 0
3 3
x x
− − + =�
Đt : ặ
cos ; 1 1
3
xt t= −
.
Ph ng trình tr thành : ươ ở
2
2 3 0t t− − + =
1 ( )
3 ( )
t n
t l
=
= −
cos 1 6
3
xx k
π
= =� �
.
0,25
0,25
0,25
0,25
4
(2)
1
(1)
2sin cos sin 2 1 0x x x+ − − =
.
2.
2 2
7
sin .cos 4 sin 2 4sin 4 2 2
x
x x x
π
� �
− = − −
� �
� �
.
Ph ng trình ươ
( ) ( )
2sin 1 1 cos 0x x− − =�
.
2sin 1 0
1 cos 0
x
x
− =
− =
1
sin 2
cos 1
x
x
=
=
2
6
52
6
2
x k
x k
x k
ππ
ππ
π
= +
= +�=
0,25
0,25+0,25
0,25
2
(1)
P.trình
1 cos 4 7
sin .cos 4 2 1 cos
2 2 2
x
x x x
π
−�� � �
− = + − −�� �
� �
� �
� �
2sin .cos 4 cos 4 4sin 2x x x x x
+ = +�
( ) ( )
2sin 1 cos 4 2 0x x+ − =�
2
16
sin 7
22
6
x k
x
x k
ππ
ππ
= − +
= −� � = +
0,25
0,25
0,25
0,25
( L u ý: H c sinh gi i cách khác, n u đúng v n cho đi m t i đa)ư ọ ả ế ẫ ể ố