ĐỀ KIỂM TRA 1 TIẾT
Chương III: Phương pháp toạ độ trong không gian - Lớp 12 CT nâng cao
I/ Mục tiêu:
a) Về kiến thức:
- Biết tính toạ độ các phép toán về véc tơ.
- Tính được tích có hướng
- Biết xét vị trí tương đối
- Tính được khoảng cách, góc
- T ìm PT m ặt cầu
B) Kỹ năng:
- Hiểu các kiến thức trong ch ương
- V ận dụng kiến thức vào thực tế giải toán
c) T ư duy v à th ái đ ộ:
- Ph át triển tư duy linh hoạt , sáng tạo
- Trung thưc, cẩn thận , chính xác
II/ Ma trận đề:
Nhận biết Thông hiểu VD thấp VD cao Tổng số
TN TL TN TL TN TL TN TL
Các phép
toán tọa
độ V Tơ
1
0,33
1
0,33
Tích vô
hướng,
có hướng
1
0 ,5
1
0,5
Khoảng
cách
2
0,66
1
1,5
3
2,16
Góc
1
0,33
1
0,33
1
0,33
3
0,99
Vị trí
tương đối
1
0,33
1
0,33
PT mặt
phẳng
1
1
1
0,33
1
1
3
2,33
Diện
tích, thể
tích
1
0,33
1
0,5
1
0,33
3
1,16
Mặt cầu
2
0,66
1
1,5
3
2,16
Tổng số
4
1,32
4
1,32
2
1,5
3
0,99
3
3,5
1
0,33
1
1
18
10
III/ĐỀ KIỂM TRA .
1/TRẮC NGHIỆM:
Câu 1:Cho tam giác ABC với A(1;-4;2), B(-3;2;-1), C(3;-1;-4). Khi đó diện tích tam giác ABC
bằng?
A) 75
B).
21 5
2 C)
85
D).95
Câu 2: Cho tam giác ABC với A(1;-4;2), B(-3;2;-1), C(3;-1;-4). Khi đó đường cao hạ từ đỉnh A
của tam giác ABC bằng?
A) 75
6 B).
730
12 C)
75
12 D). 730
6
Câu 3: Cho mặt cầu (S) : x2 + y2 + z2 –x + y – 3z + 2 = 0. Khi đó tâm I của mặt cầu là:
A). I(-1;1;-3) B).I ⎟
⎠
⎞
⎜
⎝
⎛−
2
3
;
2
1
;
2
1 C).I(1;-1;3) D).I ⎟
⎠
⎞
⎜
⎝
⎛−−
2
3
;
2
1
;
2
1
Câu 4: Cho mặt cầu (S) : x2 + y2 + z2 +2x -4y + 4z - 7 = 0. Khi đó bán kính R của mặt cầu là:
A).R =
40 B). R = 7 C). R = 4 D). R = 5.
Câu 5: Cho 3 điểm A(4;3;2), B(-1;-2;1), C(-2;2;-1). Phương trình mặt phẳng qua A và vuông góc
với BC là:
A). x - 4y + 2z + 4 = 0 B). x + 4y + 2z + 4 = 0
C). x + 4y - 2z - 4 = 0 D). x - 4y - 2z - 4 = 0.
Câu 6: Cho 2 điểm A(2;3;4) và B(1;1;2). Độ dài đoạn thẳng AB bằng?
A).3 B). 4 C). 5 D).
61 .
Câu 7: Cho điểm A(3;-1;3) và mặt phẳng (P): 2x – y – 2z + 5 = 0. Khi đó khoảng cách từ A đến
mp(P) bằng?
A).6 B). 3 C). 2 D). 5
Câu 8: Cho )2;1;1();0;3;2( −=−= ba . Tìm tọa độ của véc tơ bac 32 −= .
A). )6;9;1( −=c B). )6;9;1( −−=c C). )6;3;7( −=c D). )6;3;7( −−=c
Câu 9: Tìm góc tạo bởi hai mặt phẳng (P): x + 2y + z + 4 = 0 và (Q): -x + y + 2z + 3 = 0.
A). 300 B). 450 C). 600 D). 900.
Câu 10: Tìm cặp m, n để hai mặt phẳng sau song song:
(P): 2x + my + 3z – 5 = 0 và (Q): nx – 6y – 6z - 2 = 0.
A). m = -3, n = 4 B). m = 3, n = -4 C). m = 4, n = -3 D). m = -4, n = 3.
Câu 11: Tìm góc tạo bởi hai đường thẳng: d1:⎪
⎩
⎪
⎨
⎧
−=
−−=
+=
tz
ty
tx
21
2
3
và d2: ⎩
⎨
⎧
=−−
=−−
052
05
zx
yx .
A).1200 B). 1500 C). 600 D). 900.
Câu 12: Tìm góc tạo bởi đường thẳng d: 2
3
1
2
1
1
+
=
−
=
−
−
zyx và mặt phẳng (P):
0102 =−++ zyx .
A).1200 B). 1500 C). 600 D). 300.
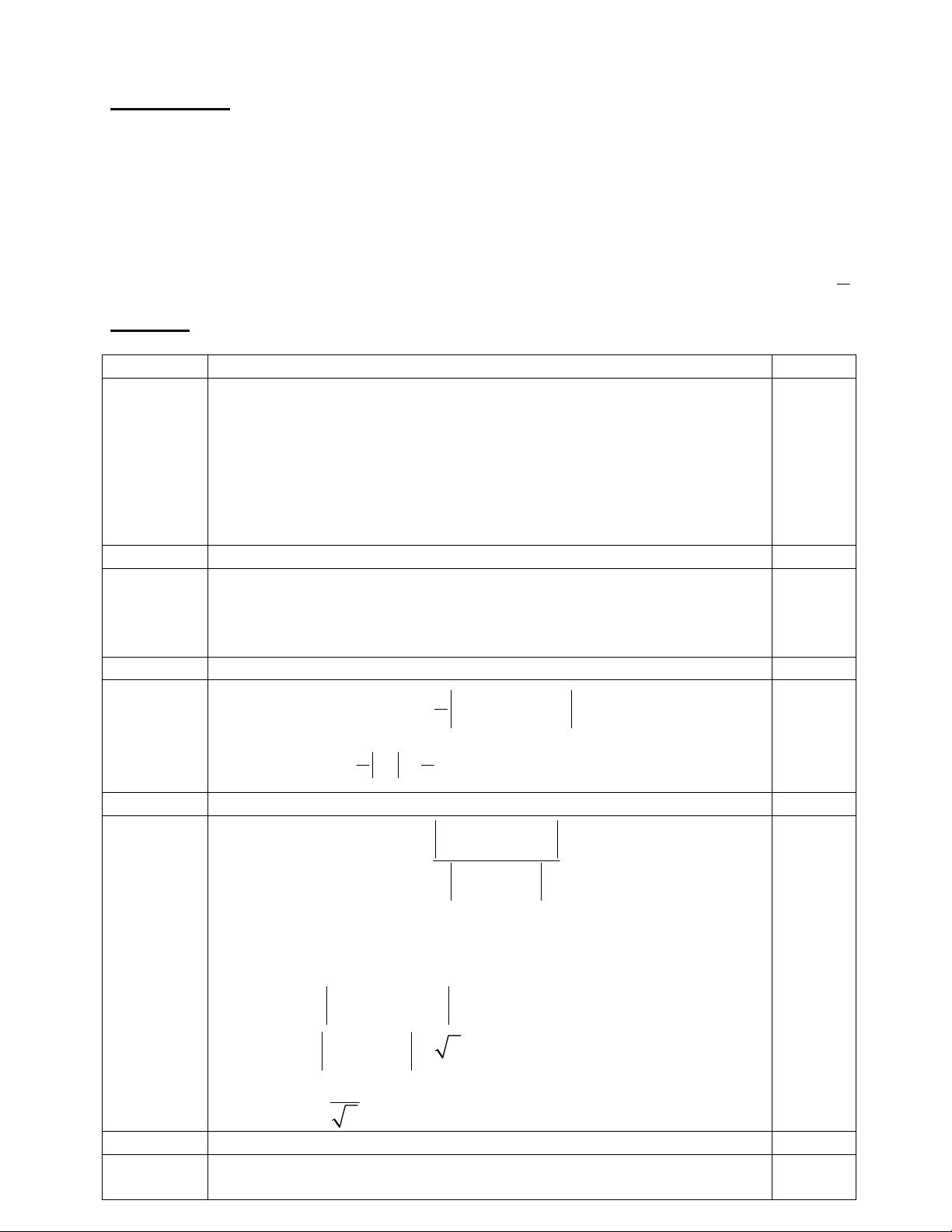
ĐÁP ÁN:
Câu 1 2 3 4 5 6 7 8 9 10 11 12
Tlời B D B C A A C A C B C D
2/T Ự LU ẬN:
Cho 4 đi ểm
(
)
1;1;1A;
(
)
1; 2;1B;
(
)
1;1; 2C;
(
)
2; 2;1D .
1)Viết PT mặt phẳng (BCD)
2)Chứng minh ABCD là một tứ diện
3)Tính thể tích tứ diện
4)Tính khoảng cách giữa AB và CD
5)Viết phương trình mặt cầu
6)Viết PT mặt phẳng chứa Oy và cắt mặt cầu theo một đường tròn có bán kính bằng 1
2
ĐÁP ÁN:
Câu 1 PT mặt phẳng (BCD) 1đ 0
+ Tính
(
)
0; 1;0BC =−
uuur
,
(
)
1; 0; 0BD =
u
uur
+ Suy ra
(
)
, 0;1;1BC BD
⎡⎤
=
⎣⎦
uuur uuur
+ Giải thích để suy ra PT mặt phẳng có dạng: 0yzD
+
+=
+ Dùng ĐK qua
(
)
1; 2;1B suy ra PT mặt phẳng (BCD) là:
30yz+−=
0,25 đ
0,25 đ
0,25 đ
0,25 đ
Câu 2 Chứng minh ABCD là một tứ diện 0đ 50
+Ta có:
(
)
0; 1;0BA =−
uuur
.Suy ra: ;1BC BD BA
⎡⎤
=
−
⎣⎦
uur uuur uuur
+Do Suy ra A,B,C,D không đồng phẳng hay ABCD tạo thành
một tứ diện
10−≠
0,25 đ
0,25 đ
Câu 3 Tính thể tích tứ diện 0đ 50
+Nêu được công thức: 1;
6
VBCBDB
⎡⎤
=⎣⎦
A
u
uur uuur uuur
+Theo trên : 11
1
66
V=−= (đvtt)
0,25 đ
0,25 đ
Câu 4 Tính khoảng cách giữa AB và CD 1đ 50
+Nêu được công thức:
;
;
A
BCD BC
d
AB CD
⎡⎤
⎣⎦
=
⎡
⎤
⎣
⎦
u
uur uuur uuur
uuuruuur
+Tính
(
)
0;1;0AB =
uuur
;
(
)
1;1; 1CD
=
−
u
uur
;
(
)
0; 1;1BC =−
u
uur
+Tính được:
(
)
;1;0AB CD
⎡⎤;1
=
−−
⎣⎦
uuuruuur
+Tính được: ;1AB CD BC
⎡⎤
=
⎣⎦
uuur uuur uuur
+Tính được: ;2AB CD
⎡⎤
=
⎣⎦
uuur uuur
+Suy ra : 1
2
d=
0,25 đ
0,25 đ
0,25 đ
0,25 đ
0,25 đ
0,25 đ
Câu 5 Phương trình mặt cầu 1đ 50
+Nêu dạng PT mặt cầu: 222
222xyz axbyczd0
+
++ + + +=
0,25 đ
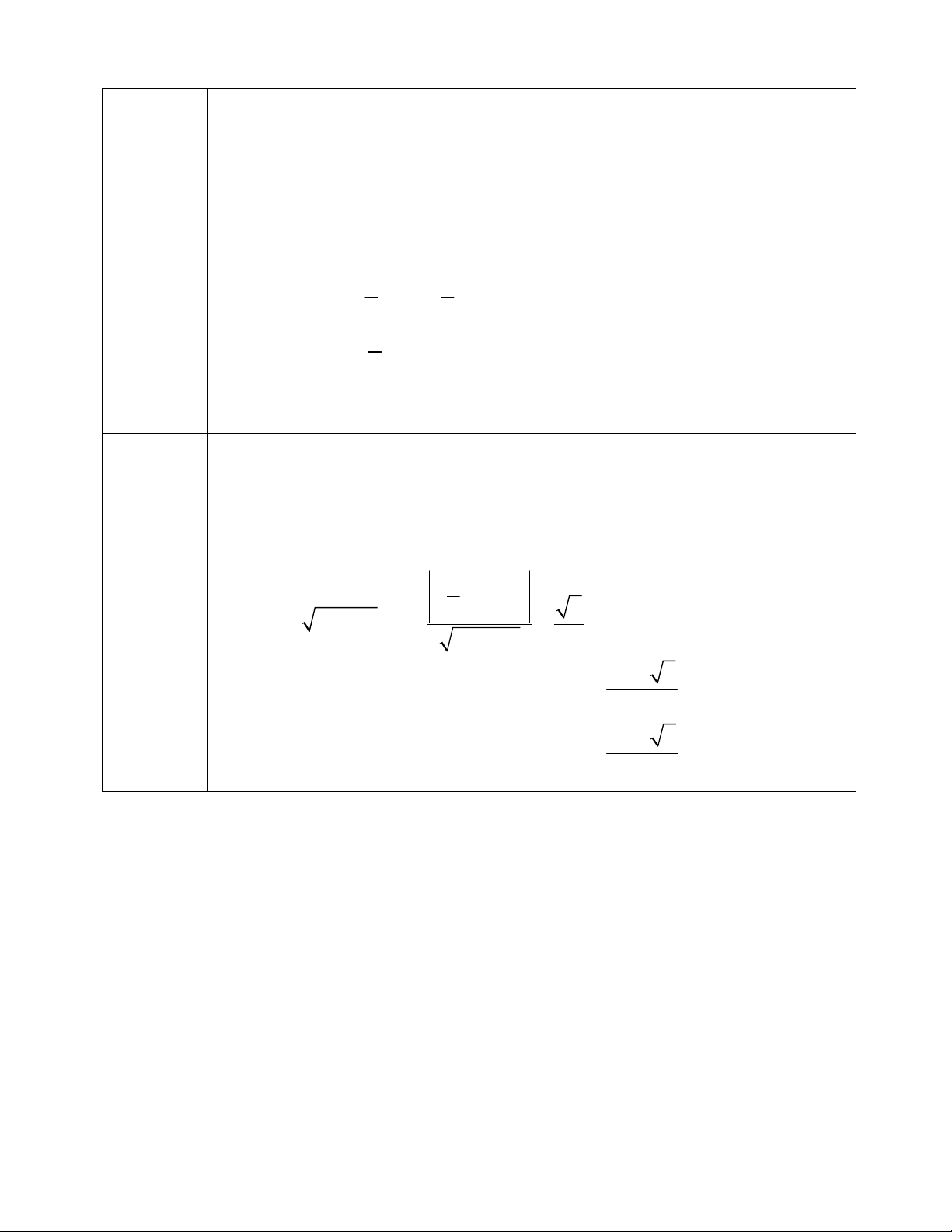
+Cho mặt cầu qua
(
)
(
)
1;1;1 ; 1; 2;1AB suy ra hai PT:
222 3
242 6
abcd
abcd
++++=
++++=
0
0
+Cho mặt cầu qua
(
)
(
)
1;1; 2 ; 2; 2;1CD suy ra hai PT:
224 6
442 9
abcd
abcd
++++=
++++=
0
0
+Giải được : 3
2
a=− ; 3
2
b
=
−;
+Giải được : 3
2
c=− ; 6d
=
+Kết luận PT mặt cầu: 222
3336xyz xyz 0
+
+−− −+=
0,25 đ
0,25 đ
0,25 đ
0,25 đ
0,25 đ
Câu 6 Viết PT mặt phẳng chứa Oy và cắt mặt cầu ĐTròn ...... 1đ 00
+Nêu dạng PT mặt phẳng : có ĐK
Ax + By + Cz + D=0
222
0
A
BC++≠
+Từ mp (P) chứa Oy ( (P) qua
(
)
(
)
0;0;0 & 0;1;0OP) Suy ra PT (P)
có dạng: 0
A
xCz+=
+Từ ĐK bài toán suy ra khoảng cách từ (P) đến tâm mặt cầu là
22
(; )dIP R r=−
⇔
22
3()
2
2
2
AC
AB
−+
=
+
+Từ đó chọn 1
A
=, tìm B suy ra hai PT là:
942
()
7
942
()
7
xz
x
⎡−0
0z
−
=
⎢
⎢
⎢+
−
=
⎢
⎣
0,25 đ
0,25 đ
0,25 đ
0,25 đ
ĐỀ KIỂM TRA CHƯƠNG I
Môn:Hình Học12- Nâng cao
Thời gian: 45 phút
MA TRẬN ĐỀ
Nhận biết Thông hiểu Vận dụng Tổng
Chủ đề TNKQ TL TNKQ TL TNKQ TL
Khái niệm về
khối đa diện.
(2 tiết)
1
1,5
1
0,5
2.0đ
Phép đối xứng
qua mp,sự bằng
nhau .
(4 tiết)
1
0,5
1
0,5
1
1,0
1
0,5
2.5đ
Phép vị tự và sự
đồng dạng…
(3 tiết)
1
0,5
1
0,5
1
1.0
2.0đ
Thể tích của khối
đa diện.
(3 tiết)
1
0,5
1
1.0
1
0,5
1
1,5
3.5đ
Tổng 2.5đ 4.0đ 3.5đ 10đ
PHẦN I:Trắc nghiệm khách quan:4đ(Mỗi câu trả lời đúng được 0,5đ)
Câu 1:(NB)Cho khối chóp có đáy là n-giác.Trong các mệnh đề sau mệnh đề nào
đúng?
A.Số cạnh của khối chóp bằng n+1;
B.Số mặt của khối chóp bằng 2n;
C.Số đỉnh của khối chóp bằng 2n+1;
D.Số mặt của khối chóp bằng số đỉnh của nó.
Câu 2(NB)Phép đối xứng qua mặt phẳng (P) biến đường thẳng d thành đường thẳng
d’ cắt d khi và chi khi:
A. d cắt (P) B. d nằm trên (P)
C. d cắt (P) nhưng không vuông góc với (P) D. d không vuông góc với (P)
Câu 3:(NB)Số mặt đối xứng của hình lập phương là
A.6 B.7
C.8 D.9
Câu 4(NB)Trong các mệnh đề sau đây,mệnh đề nào đúng?
A.Phép vị tự biến mặt phẳng thành mặt phẳng song song với nó;
B.Phép vị tự biến mặt phẳng qua tâm vị tự thành chính nó;
C.Không có phép vị tự nào biến hai điểm phân biệt A và B thành chính nó;
D.Phép vị tự biến đường thẳng thành đường thẳng song song với nó.
1