1
ĐỀ SỐ 2. ZALO 0946798489
Câu 1. Hàm số
33y x x=−
nghịch biến trên khoảng nào?
A.
( )
;1− −
. B.
( )
1;1−
. C.
( )
;− +
. D.
( )
0;+
.
Câu 2. Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
A.
3
y x x= − +
. B.
4
yx=
. C.
. D.
yx=
.
Câu 3. Cho hàm số
21
2
x
yx
+
=−
. Khẳng định nào dưới đây là đúng?
A. Hàm số có cực trị.
B. Đồ thị hàm số có tiệm cận đứng là
2x=
.
C. Đồ thị hàm số đi qua điểm
( )
1 ; 3A
.
D. Hàm số nghịch biến trên
( ) ( )
; 2 2 ; − +
.
Câu 4. Tìm các khoảng đồng biến của hàm số
42
23y x x= + −
.
A.
( )
; 0−
. B.
( )
; 1− −
và
( )
0 ; 1
.
C.
( )
0 ; +
. D.
( )
1 ; 0−
và
( )
1 ; +
.
Câu 5. Cho hàm số
23
4x
yx
−
=−
. Hãy chọn khẳng định đúng trong các khẳng định sau:
A. Hàm số nghịch biến trên .
B. Hàm số nghịch biến trên mỗi khoảng xác định.
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên mỗi khoảng xác định.
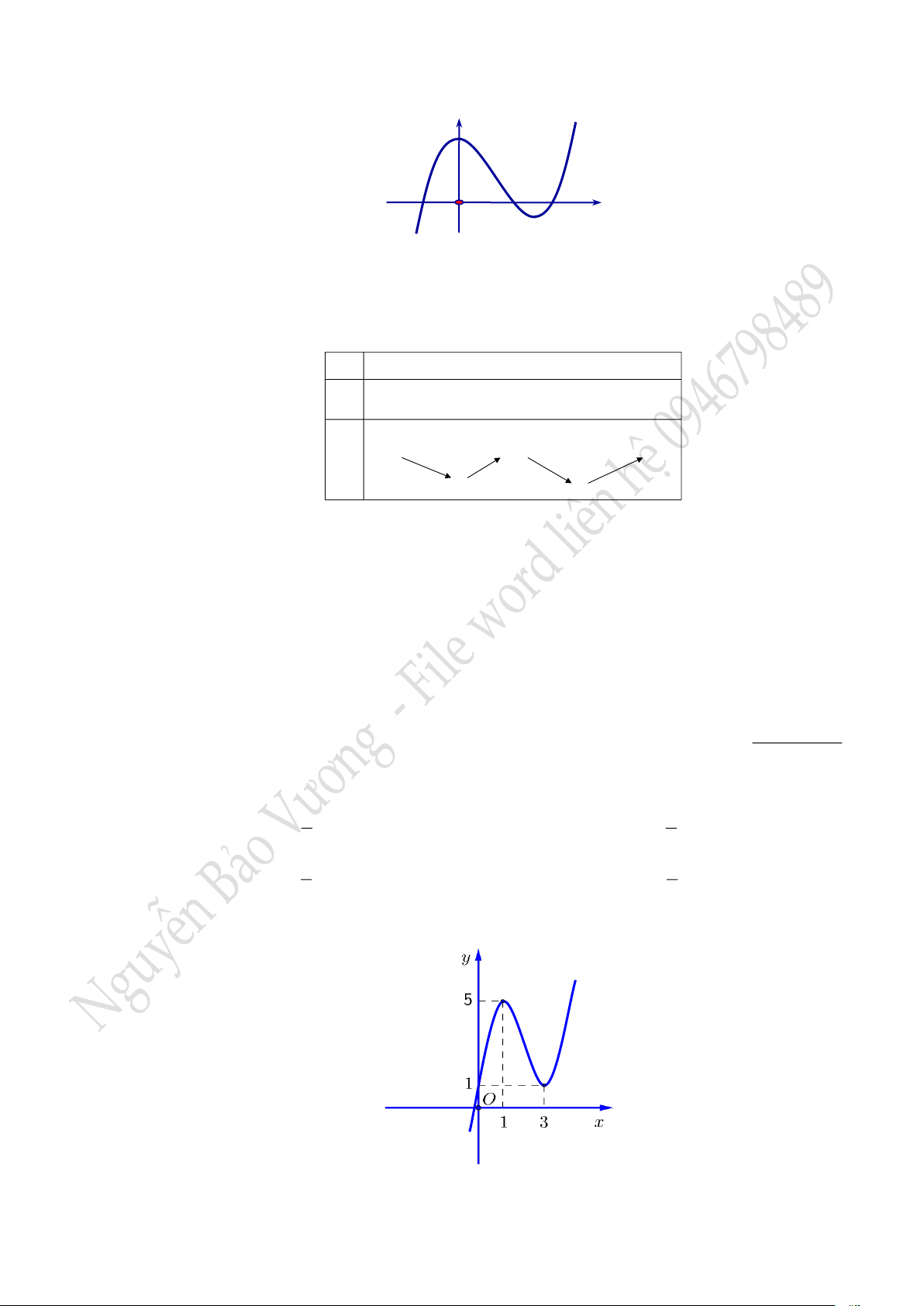
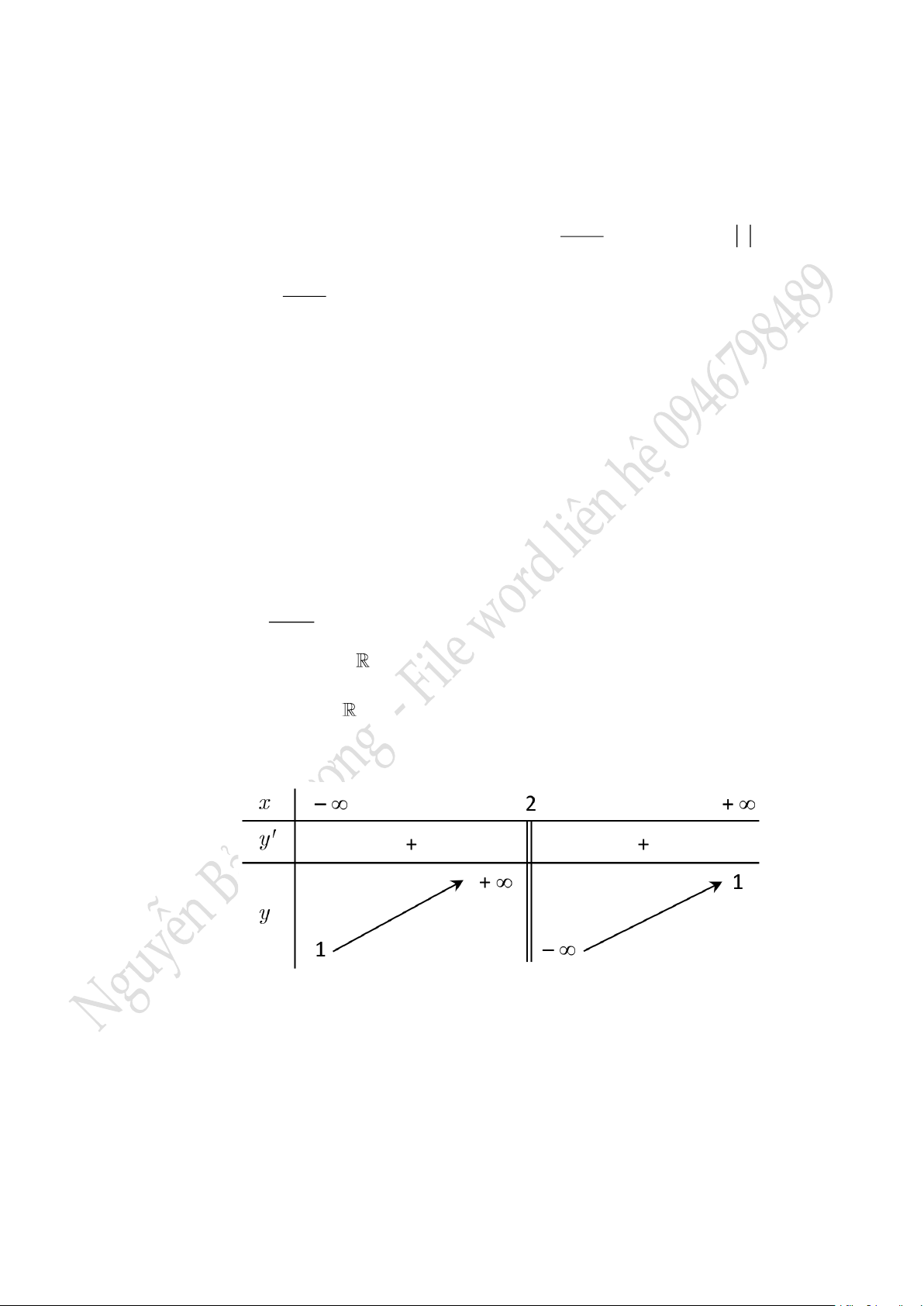
Câu 6. Cho hàm số
( )
y f x=
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây ?
A.
( )
1;+
. B.
( )
0;3
. C.
( )
;− +
. D.
( )
2;+
.
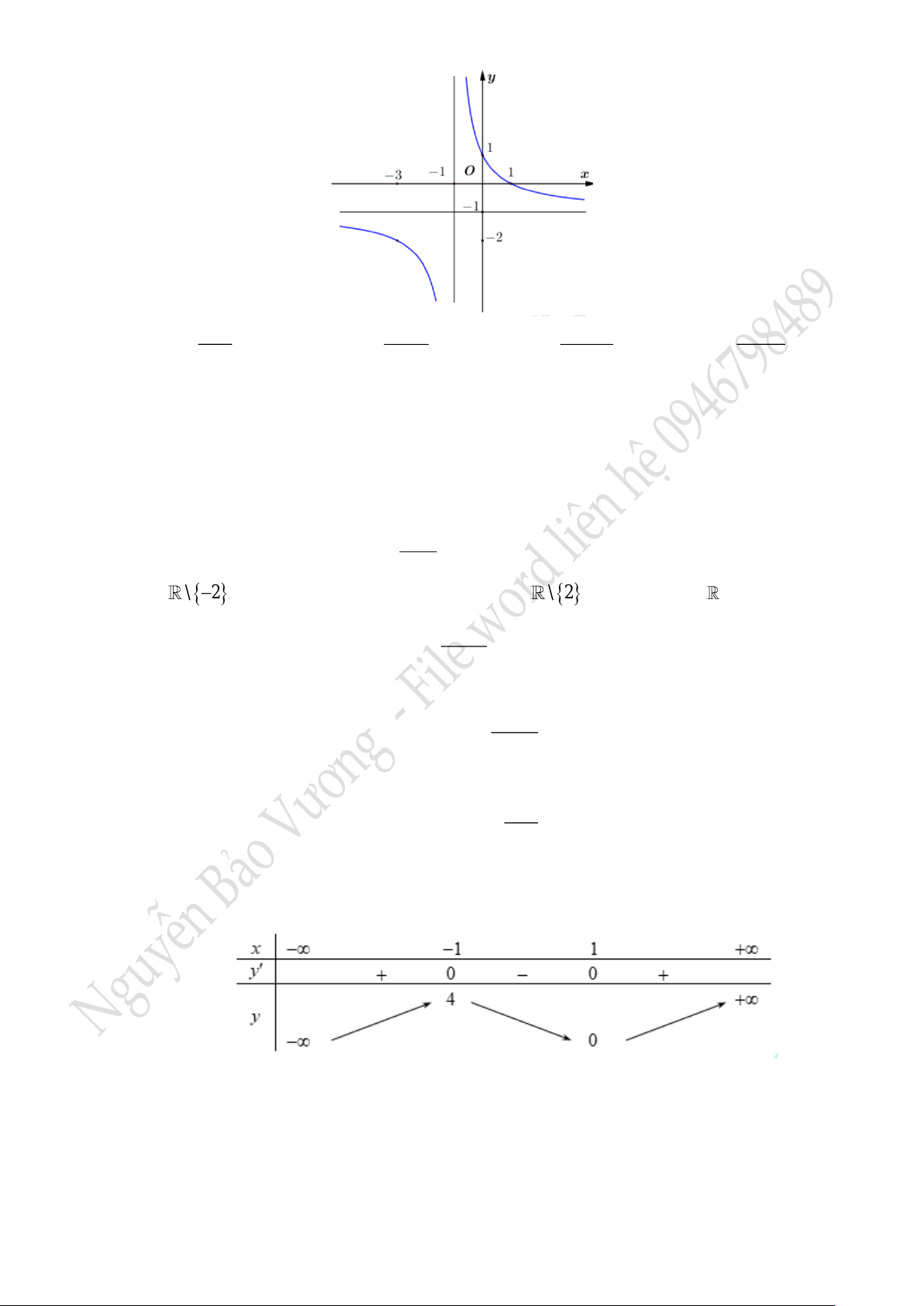
Câu 7. Đồ thị hình dưới đây là của hàm số nào?
A.
1
x
yx
−
=+
. B.
1
1
x
yx
−+
=+
. C.
21
21
x
yx
−+
=+
. D.
2
1
x
yx
−+
=+
.
Câu 8. Cho hàm số
( )
y f x=
có đạo hàm liên tục trên khoảng
K
và có đồ thị là đường
cong
( )
C
. Viết phương trình tiếp tuyến của
( )
C
tại điểm
( )
( )
;M a f a
,
( )
aK
.
A.
( )( ) ( )
y f a x a f a
= − +
. B.
( )( ) ( )
y f a x a f a
= − −
.
C.
( )( ) ( )
y f a x a f a
= − +
. D.
( )( ) ( )
y f a x a f a
= + +
.
Câu 9. Tìm tập xác định của hàm số
2
2
x
yx
−
=+
A.
\2−
. B.
( )
2;− +
. C.
\2
. D. .
Câu 10. Tìm số tiệm cận của đồ thị hàm số
34
1
x
yx
−
=−
A.
0
. B.
3
. C.
1
. D.
2
.
Câu 11. Đường tiệm cận ngang của đồ thị hàm số
24
2
x
yx
−
=+
là
A.
2y=
. B.
2x=
. C.
2x=−
. D.
2y=−
.
Câu 12. Đường tiệm cận ngang của đồ thị hàm số là
1
1
x
yx
+
=−
là
A.
1y=−
. B.
1x=
. C.
0y=
. D.
1x=−
.
Câu 13. Cho hàm số
( )
y f x=
với bảng biến thiên như hình vẽ.
Tìm giá trị cực đại
CĐ
y
và giá trị cực tiểu
CT
y
của hàm số đã cho.
A.
C4
Đ
y=
và
1
CT
y=−
. B.
C1
Đ
y=
và
0
CT
y=
.
C.
C1
Đ
y=−
và
1
CT
y=
. D.
C4
Đ
y=
và
0
CT
y=
.
3
Câu 14. Đường cong trong hình vẽ bên là đồ thị của một hàm số trong bốn hàm số ở dưới đây. Hàm số
đó là hàm số nào?
A.
42
21y x x= − + +
. B.
32
33y x x= − +
.
C.
42
21y x x= − +
. D.
32
31y x x= − + +
.
Câu 15. Cho hàm số
( )
fx
có bảng biến thiên như hình vẽ. Kết luận nào sau đây là sai?
A. Hàm số có 3 điểm cực trị. B. Hàm số đạt cực tiểu tại
1.x=−
C. Hàm số đồng biến trên
( )
4; 3−−
. D. Hàm số nghịch biến trên
( )
0;1
.
Câu 16. Cho hàm số
( )
42
13y m x mx= + − +
. Tìm tất cả các giá trị thực của tham số
m
để hàm số có ba
điểm cực trị.
A.
( )
)
; 1 0;m − − +
. B.
( )
1;0m−
.
C.
(
)
; 1 0;m − − +
. D.
( ) ( )
; 1 0;m − − +
.
Câu 17. Tìm tất cả các giá trị thực của tham số
m
để giá trị nhỏ nhất của hàm số
2
23
x m m
yx
+−
=−
trên đoạn
0;1
bằng
2−
.
A.
1m=
hoặc
1
2
m=−
. B.
3m=
hoặc
5
2
m=−
.
C.
1m=−
hoặc
3
2
m=
. D.
2m=
hoặc
3
2
m=−
.
Câu 18. Cho hàm số
( )
32
y f x ax bx cx d= = + + +
có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A.
0a
,
0b
,
0c
,
0d
. B.
0a
,
0b
,
0c
,
0d
.
x
y
-∞
+∞
+∞
+∞
-1
-4 -4
0
-3
1
y’ 00
0
--+ +
O
x
y
C.
0a
,
0b
,
0c
,
0d
. D.
0a
,
0b
,
0c
,
0d
.
Câu 19. Một chất điểm chuyển động có phương trình chuyển động là
32
6 17s t t t= − + +
, với
( )
ts
là
khoảng thời gian tính từ lúc vật bắt đầu chuyển động và
( )
sm
là quãng đường vật đi được trong khoảng
thời gian đó. Trong khoảng thời gian 8 giây đầu tiên, vận tốc
( )
/v m s
của chất điểm đạt giá trị lớn nhất
bằng
A.
17 /ms
. B.
36 /ms
. C.
29 /ms
. D.
26 /ms
.
Câu 20. Tìm khoảng đồng biến của hàm số
32
31y x x= − + −
.
A.
( )
0;3
. B.
( )
1;3−
. C.
( )
2;0−
. D.
( )
0;2
.
Câu 21. Cho hàm số
( )
y f x=
liên tục trên , đồ thị của đạo hàm
( )
fx
như hình vẽ sau:
Trong các mệnh đề sau, mệnh đề nào sai?
A.
f
đạt cực tiểu tại
0x=
. B.
f
đạt cực tiểu tại
2x=−
.
C.
f
đạt cực đại tại
2x=−
. D. Cực tiểu của
f
nhỏ hơn cực đại.
Câu 22. Số đường tiệm cận của đồ thị hàm số
2
24
1
x
yx
−
=−
là
A. 4. B. 2. C. 3. D. 1.
Câu 23. Đồ thị hàm số
2
5 1 1
2
xx
yxx
+ − +
=−
có tất cả bao nhiêu đường tiệm cận?
A.
3
. B.
1
. C.
0
. D.
2
.
Câu 24. Cho hàm số
( )
y f x=
có đạo hàm
( ) ( )( )
3
21 13 15f x x x x
= − −
. Khi đó số điểm cực trị của
hàm số
2
54
x
yf
x

=
+

là
A.
2
. B.
5
. C.
6
. D.
3
.
Câu 25. Phương trình
( )
( )
2
32
11x x x m x+ + = +
có nghiệm thực khi và chỉ khi
A.
14
125
m−
. B.
13
44
m−
. C.
3
64
m−
. D.
4
3
m
.
Câu 26. Cho hàm số
ax b
yxc
+
=−
có đồ thị như hình vẽ bên.
5
Tìm khẳng định đúng trong các khẳng định sau
A.
0, 0,c 0ab
. B.
0, 0,c 0ab
. C.
0, 0,c 0ab
. D.
0, 0,c 0ab
.
Câu 27. Cho hàm số
2
1
x
yx
+
=+
có đồ thị
( )
C
. Gọi
d
là khoảng cách từ giao điểm hai tiệm cận của đồ
thị
( )
C
đến một tiếp tuyến của
( )
C
. Giá trị lớn nhất của
d
có thể đạt được là
A.
2
. B.
33
. C.
3
. D.
22
.
Câu 28. Cho hàm số
()y f x=
có đồ thị
()y f x
=
như hình vẽ. Xét hàm số
32
1 3 3
( ) ( ) 2018
3 4 2
g x f x x x x= − − + +
. Mệnh đề nào dưới đây đúng?
A.
[ 3;1]
min ( ) (1)g x g
−=
. B.
[ 3;1]
min ( ) ( 1)g x g
−=−
.
C.
[ 3;1]
min ( ) ( 3)g x g
−=−
. D.
[ 3;1]
( 3) (1)
min ( ) 2
gg
gx
−
−+
=
.
Câu 29. Tìm tập hợp tất cả các giá trị
m
sao cho hàm số
2
sin
cos
mx
yx
−
=
nghịch biến trên
0; 6



.
A.
1m
. B.
2m
. C.
5
4
m
. D.
0m
.
Câu 30. Cho hàm số
( )
21
1
x
yC
x
+
=+
,
I
là tâm đối xứng của đồ thị
( )
C
và
( )
;M a b
là 1 điểm thuộc đồ
thị
( )
C
. Tiếp tuyến của
( )
C
tại
( )
;M a b
cắt 2 đường tiệm cận của đồ thị
( )
C
lần lượt tại 2 điểm
,AB
.
Để tam giác
IAB
có bán kính đường tròn nội tiếp lớn nhất thì tổng
ab+
gần nhất với số nào dưới đây.
A.
5
. B.
3−
. C.
0
. D.
3
.
O
x
y