Trang 1
ĐỀ SỐ 7. ZALO 0946798489
ĐỀ BÀI
Câu 1. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
32
11
23
33
y x x x= − + −
trên
đoạn
0;2
. Tính tổng
S M m=+
.
A.
1
3
S=
. B.
4
3
S=
. C.
1S=
. D.
.
Câu 2. Đường thẳng
6 10yx=−
cắt đồ thị hàm số
32
41y x x= − −
tại mấy điểm?
A.
3
. B.
2
. C.
4
. D.
1
.
Câu 3. Tìm tất cả các giá trị của tham số
m
để hàm số
32
11
3
y x mx x= − + −
có hai điểm cực trị
12
,xx
thỏa mãn
22
1 2 1 2 9x x x x+ − =
A.
3m=
. B.
3m=
. C.
23m=
. D.
0m=
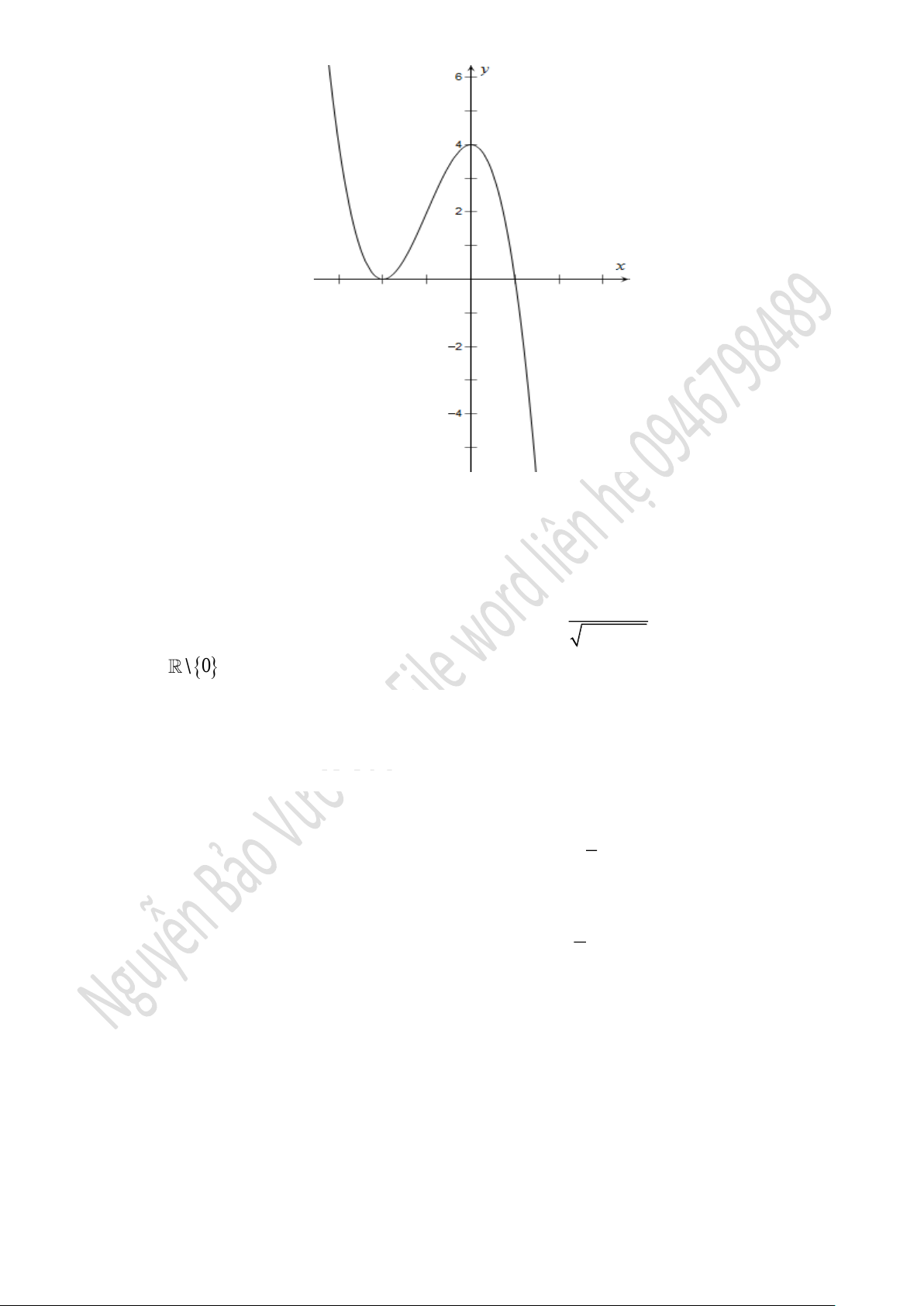
Câu 4. Cho hàm số
( )
y f x=
có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số
( )
y f x=
có bao nhiêu
điểm cực trị.
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 5. Cho hàm số
y x sinx=−
.Khẳng định nào dưới đây là ĐÚNG ?
A. Hàm số nghịch biến trên khoảng (
;0−
).
B. Hàm số đồng biến trên .
C. Hàm số đồng biến trên khoảng (
0;+
) và nghịch biến trên khoảng (
;0−
).
D. Hàm số nghịch biến trên khoảng (
0;+
) .
Câu 6 . Có bao nhiêu số nguyên
m
để hàm số
32
11
3
y x mx x= − + −
đồng biến trên ?
A.
2
. B.
4
. C.
3
. D. 5.
Câu 7. Hàm số nào dưới đây nghịch biến trên khoảng
( )
0;+
?
A.
42
21y x x= − − +
. B.
21
1
x
yx
+
=−
. C.
331y x x= + −
. D.
21yx=+
.
Câu 8. Tìm giá trị cực tiểu của hàm số
32
31
22
y x x= − +
.
A.
1
2
CT
y=
. B.
1
2
CT
y=−
. C.
1
CT
y=
. D.
0
CT
y=
.
Trang 2
Ta có:
( )
1 3 0y =
Hàm số đạt cực tiểu tại
1x=
và
( )
10
CT
yy==
.
Câu 9. Cho
( ) ( )
,y f x y g x==
là các hàm số liên tục trên
;ab
. Gọi
( )
;
min
ab fx
=
,
( )
;
min
ab gx
=
.
Phát biểu nào sau đây luôn ĐÚNG?
A.
( ) ( )
;
min
ab f x g x

+ = +


. B.
( ) ( )
;
min
ab f x g x

− = −


.
C.
( ) ( )
;
min . .
ab f x g x

=


. D.
( )
;
min 5 5
ab gx
=


.
Câu 10. Tìm tập hợp các giá trị của
m
để phương trình
3
4 3 2 3 0x x m− − + =
có đúng một nghiệm.
A.
( ) ( )
;1 2;− +
. B.
( )
2;+
.
C.
( ) ( )
;2 4;− +
. D.
( )
;2− −
.
Câu 11. Cho hàm số
12
2x
yx
−
=−
có đồ thị là
( )
C
Phát biểu nào dưới đây đúng?
A. Đồ thị
( )
C
có tiệm cận đứng là đường thẳng
2;x=−
tiệm cận ngang là đường thẳng
2.y=
B. Đồ thị
( )
C
có tiệm cận đứng là đường thẳng
2;y=−
tiệm cận ngang là đường thẳng
2.x=
C. Đồ thị
( )
C
có tiệm cận đứng là đường thẳng
2;x=
tiệm cận ngang là đường thẳng
2.y=
D. Đồ thị
( )
C
có tiệm cận đứng là đường thẳng
2;x=
tiệm cận ngang là đường thẳng
2.y=−
Câu 12. Tìm tất cả các giá trị của tham số
m
để hàm số
3 2 2
3 9 1y x x m x= − − +
đạt cực đại tại
1.x=−
A.
1.m=−
B.
1.m=
C.
0.m=
D.
1.m=
Câu 13. Cho hàm số
( )
y f x=
có bảng biến thiên như hình bên dưới. Phát biểu nào dưới đây là SAI?
A. Đồ thị hàm số nhận gốc tọa độ O là điểm cực tiểu.
B. Đồ thị hàm số có ba đường tiệm cận.
C. Đồ thị hàm số cắt đường thẳng
=2017y
tại hai điểm phân biệt.
D. Đồ thị hàm số nghịch biến trên khoảng
( )
−;0
và đồng biến trên khoảng
( )
+0;
.
Câu 14. Cho hàm số
( )
y f x=
liên tục trên và có bảng biến thiên như hình bên dưới. Phát biểu nào
dưới đây là SAI?
Trang 3
A. Hàm số đạt cưc đại tại
=1
2
x
.
B. Hàm số có giá trị cực tiểu bằng
1
3
.
C. Hàm số có hai điểm cực trị.
D. Hàm số đạt cực tiểu tại
=0x
.
Câu 15. Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
42
( 1) 1y x m x= − + − +
có ba điểm cực trị
tạo thành một tam giác đều.
A.
3
1 2 3m=
. B.
3
1 2 3m=+
. C.
3
1 2 3m=−
. D.
1m=
.
Câu 16. Tìm giá trị nhỏ nhất của hàm số
cos3 4 2017y x x= + +
trên đoạn
0;
A.
2018
. B.
2017
. C.
2020
. D.
2019
.
Câu 17. Tiếp tuyến của đồ thị hàm số
32
1
x
yx
−
=+
tại điểm
( )
0; 2A−
cắt trục hoành và trục tung lần lượt
tại
M
và
.N
Tính diện tích tam giác
.OMN
A.
4
5
OMN
S=
. B.
2
5
OMN
S=
. C.
2
OMN
S=
. D.
5
OMN
S=
.
Câu 18. Cho hàm số
32
1161
32
= − − + −y x x x
. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng
( )
;2−
.
B. Hàm số đồng biến trên khoảng
( )
3;+
.
C.Hàm số đồng biến trên khoảng
( )
3;2−
.
D. Hàm số nghịch biến trên khoảng
( )
3;2−
.
Câu 19. Cho hàm số
( )
y f x=
liên tục trên và có đạo hàm
( )
( )( )
( )
2 2 2
' 4 3 2 3f x x x x x x= − + + +
.
Hàm số có bao nhiêu điểm cực tiểu?
A.
3
. B.
2
. C.
1
. D.
0
.
Câu 20: Cho hàm số
21
2
x
yx
−
=−
. Khẳng định nào dưới đây là SAI ?
A. Hàm số nghịch biến trên
( ;2) (2; )− +
.
B. Hàm số nghịch biến trên khoảng
( ;0)−
. .
C. Hàm số nghịch biến trên khoảng
(0;1)
.
D. Hàm số nghịch biến trên khoảng
(2; )+
.
Câu 21 . Đường cong hình bên là đồ thị của một hàm số được liệt kê ở bốn phương án A,B,C,D dưới
đây.Hỏi hàm số đó là hàm số nào?
Trang 4
A.
32
34y x x= − − +
. B.
32
34y x x= + +
. C.
32
34y x x= − +
. D.
32
34y x x= − + +
.
Câu 22. Biết đồ thị hàm số
42
23y x x= − +
cắt đồ thị hàm số
2
35yx=−
tại điểm duy nhất là
M
. Tìm
tung độ của
M
A.
5
M
y=−
. B.
2
M
y=−
. C.
3
M
y=
. D.
0
M
y=
.
Câu 23. Tìm tập hợp tất cả các giá trị của m để đồ thị hàm số
2
13
32
x
ymx
−
=−
có hai tiệm cận ngang.
A.
\0
. B.
( )
0;+
. C.
( )
;0−
. D.
.
Câu 24. Một người bán gạo muốn đóng một thùng tôn đựng gạo thể tích không đổi bằng
3
5Vm=
, thùng
tôn hình hộp chữ nhật có đáy là hình vuông, không nắp. Trên thị trường, giá tôn làm đáy thùng
là
2
10$ /1m
, giá tôn làm mặt xung quanh của thùng là
2
8$ / 1m
. Hỏi người bán gạo đó đóng
thùng đựng gạo với cạnh đáy bằng bao nhiêu sao cho chi phí mua nguyên liệu là nhỏ nhất?
A.
1.m
B.
1,5 .m
C.
3.m
D.
2.m
Câu 25. Tìm tập hợp tất cả các giá trị của tham số m để hàm số
( ) ( )
32
12 2 1
3
y x m x m x m= + − + − +
nghịch biến trên khoảng
( )
0;3
.
A.
(
;2−
. B.
( )
1;5
. C.
1
;2

−

. D.
0;1
.
Trang 5
BẢNG ĐÁP ÁN
1.D
2.D
3.B
4.B
5.B
6.C
7.A
8.D
9.D
10.A
11.C
12.B
13.D
14.A
15B
16.A
17.B
18.C
19.B
20.A
21.A
22.C
23.C
24.D
25.C
GIẢI CHI TIẾT
Câu 1. Gọi
,Mm
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
32
11
23
33
y x x x= − + −
trên
đoạn
0;2
. Tính tổng
S M m=+
.
A.
1
3
S=
. B.
4
3
S=
. C.
1S=
. D.
.
Lời giải
Chọn D
TXĐ:
D=
.
21
4 3 0 3
x
y x x y x
=

= − + = =
. Với
0;2x
thì
1x=
thỏa mẫn.
Ta có:
( ) ( ) ( )
11
0 , 1 1, 2
33
f f f= − = =
.
Vậy
1M=
và
1 1 2
1
3 3 3
mS= − = − =
.
Câu 2. Đường thẳng
6 10yx=−
cắt đồ thị hàm số
32
41y x x= − −
tại mấy điểm?
A.
3
. B.
2
. C.
4
. D.
1
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm:
32
4 1 6 10 1x x x x− − = − =
.
Vậy đường thẳng
6 10yx=−
cắt đồ thị hàm số
32
41y x x= − −
tại 1 điểm
Câu 3. Tìm tất cả các giá trị của tham số
m
để hàm số
32
11
3
y x mx x= − + −
có hai điểm cực trị
12
,xx
thỏa mãn
22
1 2 1 2 9x x x x+ − =
A.
3m=
. B.
3m=
. C.
23m=
. D.
0m=
Lời giải
Chọn B
Ta có
2
' 2 1y x mx= − +
.
Để hàm số có hai điểm cực trị
12
,xx
thỏa mãn
22
1 2 1 2 9x x x x+ − =
thì:
( ) ( )
( ) ( )
2
222
1 2 1 2
'0 10 ; 1 1; 3
392 3.1 9 3
mmm
x x x x mm
 −
− − +
=
+ − = −= =