S GIÁO D C - ĐÀO T OỞ Ụ Ạ Đ THI CH N H C SINH GI I B C PTTHỀ Ọ Ọ Ỏ Ậ
TH A THIÊN HU Ừ Ế NĂM H C 2000-2001.Ọ
----------------------- -------------------------------------------------
Đ CHÍNH TH C Ề Ứ MÔN: TOÁN B NG B VÒNG 1. Ả
SBD: (180 phút, không k th i gian giao đ )ể ờ ề
------------------------------------------------------------------------------------------------------------
Bài 1: (2.5 đi m) Cho ph ng trình:ể ươ sin2x + cos2x + 4sin3x – 4sinx + 2mcosx + 1 = 0.
Tìm giá tr c a m đ cho ph ng trình có t p nghi m là:ị ủ ể ươ ậ ệ
T = { x /
x k ,k Z
2
π
= + π ∈
}.
Bài 2: (2.5 đi m) Gi i ph ng trình: ể ả ươ
2
x (2x 1) 2x 1
16 2.4 0
− −
− =
.
Bài 3: (2.5 đi m) Cho t di n ABCD cóhai c nh đ i b ng b, c và các c nh còn l i b ng a.ể ứ ệ ạ ố ằ ạ ạ ằ
a/ Tìm giá tr nh nh t c a t ng các kho ng cách t m t đi m tùy ý trong không gian đ nị ỏ ấ ủ ổ ả ừ ộ ể ế
các đ nh c a t di n.ỉ ủ ứ ệ
b/ Gi s t di n ABCD thay đ i v trí trong không gian nh ng có ba đ nh A, B, C l n l tả ử ứ ệ ổ ị ư ỉ ầ ượ
trên m t c u c đ nh và đ ng tâm.ở ặ ầ ố ị ồ
Ch ng minh r ng đ nh D luôn trong m t hình c u c đ nh khi đ dài a, b, c thay đ i th aứ ằ ỉ ở ộ ầ ố ị ộ ổ ỏ
các gi đã cho.ả
Bài 4: (2.5 đi m) Tìm tham s a đ cho h sau có nghi m:ể ố ể ệ ệ
2
a(x a) (x 2 2) 1 0
x a 0
− − + ≤
> >
S GIÁO D C - ĐÀO T OỞ Ụ Ạ KỲ THI CH N H C SINH GI I B C PTTHỌ Ọ Ỏ Ậ
TH A THIÊN HU Ừ Ế NĂM H C 2000-2001.Ọ
-----------------------
H NG D N CH M Đ THI MÔN TOÁNƯỚ Ẫ Ấ Ề
B NG B – VÒNG 2.Ả
Bài 1: (2.5 đi m)ể
•sin2x + cos2x + 4sin3x – 4sinx + 2mcosx + 1 = 0 (1)
⇔ 2sinxcosx + 2cos2x + 4sinx(sin2x + 1) + 2mcosx = 0 ⇔ cosx(sinx + cosx -2sinxcosx +m) = 0
•
cos x 0 x k ,k Z
2
sin x cos x 2sin x cos x m 0 sin x cos x 2sinxcosx + m = 0 (2)
π
== + π ∈
⇔ ⇔
+ − + =
+ −
•Do đó (1) có t p nghi m T = { x / ậ ệ
x k ,k Z
2
π
= + π ∈
}khi ch khi (2) ch có nghi m thu c T ho c (2)ỉ ỉ ệ ộ ặ
vô nghi m.ệ
•Xét ph ng trình (2): sinx + cosx – 2sinxcosx + m = 0 ươ
2
t sin x cos x 2 sin(x )
4
f(t) = t t m (3) (I)
| t | 2 (4)
π
= + = +
⇔ − −
≤
•Ph ng trình (2) có nghi m thu c Tươ ệ ộ
cos x 0 m 1
sin x 1 m 1
= =
⇒ ⇔
= ± = −
Th l i: m = 1: Khi đó (3) ử ạ ⇔ t2 – t – 2 = 0 ⇔ t = -1 ho c t = 2.ặ
H (I) tr thành: ệ ở
x k2
1
2 sin(x ) 1 sin(x )
4 4 x k2
22
= π+ π
π π
+ = − ⇔ + = ⇔ π
= − + π
V y T không ph i là t p nghi m c a ph ng trình đã cho.ậ ả ậ ệ ủ ươ
Th l i: m = -1: Khi đó (3) ử ạ ⇔ t2 – t = 0 ⇔ t = 0 ho c t = 1.ặ
H (I) tr thành: ệ ở
V y T không ph i là t p nghi m c a ph ng trình đã cho.ậ ả ậ ệ ủ ươ
•Ph ng trình (2) vô nghi m:ươ ệ
f(t) là tam th c b c hai có ứ ậ ∆ = 5 + 4m,
S 1
2 2
=
, kí hi u tệ1, t2 là hai nghi m c a f(t) = 0.ệ ủ
Do
S
2 2
2
− < <
nên h (1) vô nghi m khi ch khi:ệ ệ ỉ
∆ < 0 ho c ặ
1 2
0f(- 2) 0
5 5
m hay m hay m > 1+ 2
4 4
t 2 2 t f( 2) 0
∆ >
<
⇔ < − ⇔ < −
< − < <
<
V y các giá tr m th a đ bài là: ậ ị ỏ ề
5
m hay m > 1+ 2
4
< −
.
Bài 2: (2.5 đi m)ể
•Bi n đ i ph ng trình:ế ổ ươ
2 2
x (2x 1) 2x 1 4x (2x 1) 4x 1 3 2
16 2.4 0 2 2 8x 4x 4x 1 0 (1)
− − − −
− = ⇔ = ⇔ − − + =
•Đa th c f(t) =ứ
3 2
8x 4x 4x 1 0− − + =
có t i đa 3 nghi m và ta có: f(-1)=-7; f(0)=1; f(1/2)=-1,f(1)=1ố ệ
f(t) liên t c trên kho ng (-1;1) và f(-1).f(0) < 0, f(0).f(1/2) < 0, f(1/2).f(1) < 0 nên f(x) = 0 có 3ụ ả
nghi m trên kho ng (-1;1).ệ ả
•Do f(t) = 0 có đúng 3 nghi m trong kho ng (-1;1), nên ta có th đ t x = cosa v i 0 < a < ệ ả ể ặ ớ π.
•Ph ng trình (1) tr thành: ươ ở
8cos3a – 4cos2a – 4cosa + 1 = 0 ⇔ 4cosa(2cos2a – 1) = 4(1 – sin2a) – 1
⇔ 4cosa.cos2a = 3 – 4sin2a ⇔ 4sina.cosa.cos2a = 3sina – 4sin3a ( do sina > 0)
⇔ sin4a = sin3a ⇔
4a 3a k2 (k Z)
4a 3a k2
= + π
∈
= π− + π
( v i 0 < a < ớπ)
⇔
3 5
a hay a = hay a =
7 7 7
π π π
=
.
Câu 3 ( 2.5 đ)
Câu a (1.75 đ)
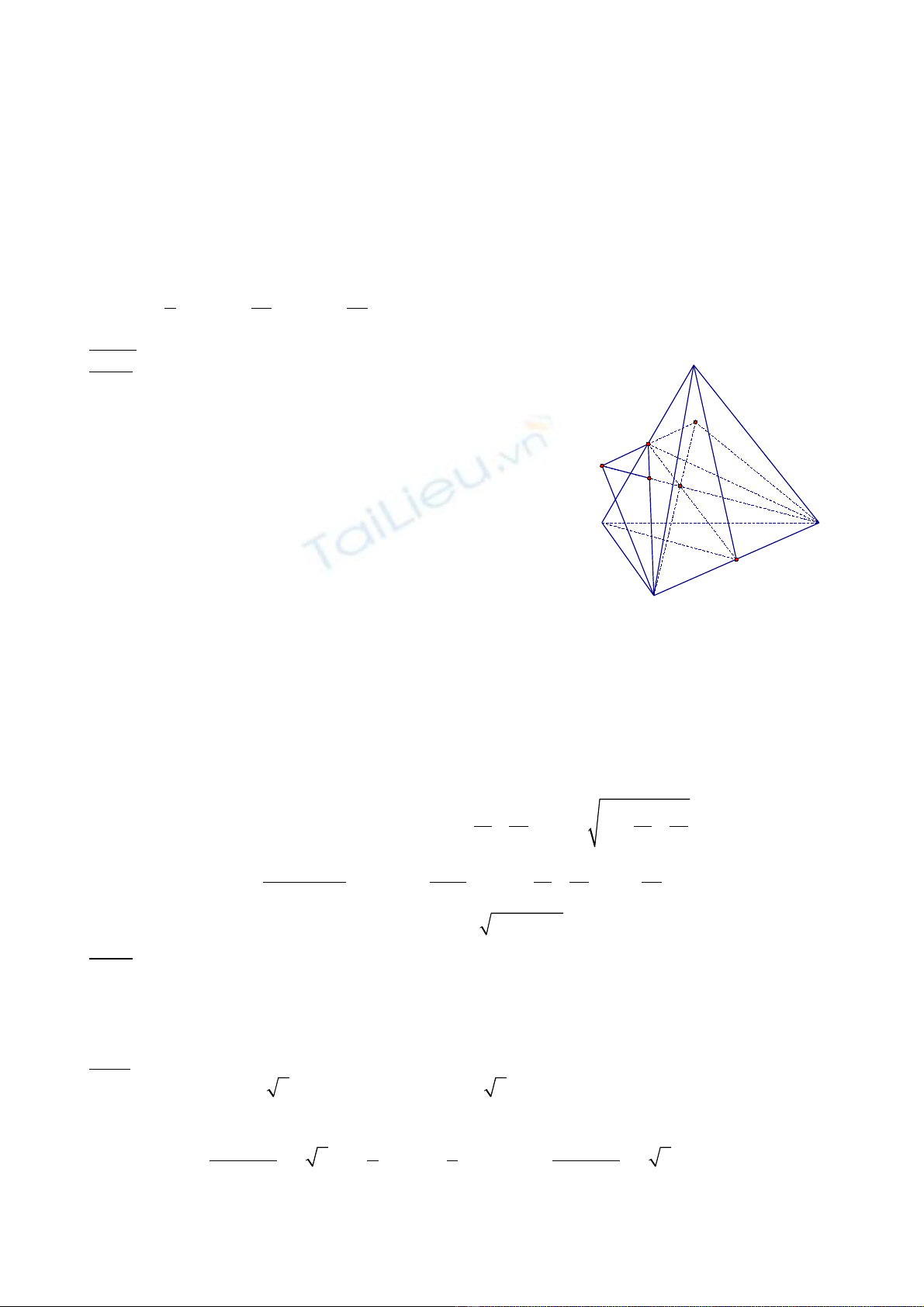
•Ta có th gi s AD = b, BC = c và các c nh còn l iể ả ử ạ ạ
b ng a. G i I, J l n l t là trung đi m c a các c nh ằ ọ ầ ượ ể ủ ạ
AD, BC. Ta d dàng suy ra vuông góc v i AD và ễ Ị ớ
BC và IJ chính là tr c đ i x ng c a t di n.ụ ố ứ ủ ứ ệ
•L y M tùy ý trong không gian, M’ là đi m đ i x ngấ ể ố ứ
c a M qua IJ suy ra trung đi m K c a MM’ chính làủ ể ủ
hình chi u c a M trên đ ng th ng IJ và ta có:ế ủ ườ ẳ
•2(MA + MB + MC + MD) = MA + MB + MC + MD
+ M’A + M’B+M’C+M’D
= (MA + M’A) + (MB + M’B) + (MC + M’C) + (MD + M’D)
≤ 2KA + 2KB + 2KC + 2KD (1).
( Do tính ch t: trung tuy n c a m t tam giác thì bé h n n a t ngấ ế ủ ộ ơ ữ ổ
c a hai c nh cùng xu t phát t m t đ nh c a nó).ủ ạ ấ ừ ộ ỉ ủ
•Do đó: MA + MB + MC + MD ≤ KA + KB + KC + KD. Bài toán tr thành tìm đi m K trên IJ saoở ể
cho KA + KB + KC + KD bé nh t.ấ
•Trong m t ph ng (BCI) d ng hình thang BCD’A’ sao cho IJ là trung đi m c a hai đáy và IA = IA’,ặ ẳ ự ể ủ
ID = ID’. Ta th y r ng: v i K tùy ý trên thì KA = KA’ và KD = KD’. Do đó:ấ ằ ớ Ị
KA + KB + KC + KD = KA’ + KB + KC + KD’ = (KA’ + KC) + (KB + KD’) ≤ A’C + BD’.
•V y KA + KB + KC + KD nh nh t khi K chính là giao đi m Kậ ỏ ấ ể 0 c a hai đ ng chéo A’C và BD’.ủ ườ
•Tính IJ: IJ2 = DJ2 – ID2 = DC2 – JC2 – ID2 = a2 -
2 2 2 2
2
c b c b
IJ a
4 4 4 4
− ⇒ = − −
.
•Tính BD’:
2 2 2 2
2 2 2 2
BC A'D' b c c b bc
BD' IJ a a
2 2 4 4 2
+ +
= + = + − − = +
÷ ÷
.
•T ng các kho ng cách nh nh t là: d = 2BD’ = ổ ả ỏ ấ
2
4a 2bc+
.
Câu a (0.75 đ)
•G i rọ1, r2, r3 là bán kính các m t c u tâm O và l n l t đi qua các đ nh A, B, C. Ta có:ặ ầ ầ ượ ỉ
•OD < OC + DC < OC + AB < OC + OA + OB = r1 + r2 + r3. Do đó D trong hình c u c đ nh tâm O,ở ầ ố ị
bán kính R = r1 + r2 + r3.
Bài 4: (4.0 đi m)ể
•
2 2 2
a(x a) (x 2 2) 1 0 (x a) ax - 2 2a(x a) 1 0
x a 0 x a 0
− − + ≤ − − + ≤
⇔
> > > >
•
2 2
1 1 1 1
x 2 2 (x a) (x a) a 2 2 (1)
(x a) a 2 2 (x a) a
x a 0 x a 0 (2)
+ ≤ − + − + + ≤
− −
⇔ ⇔
> > > >
•Do (2) nên x – a và a là hai s d ng, áp d ng b t đ ng th c Cô-si cho 4 s d ng ta đ c:ố ươ ụ ấ ẳ ứ ố ươ ượ
I
J
A
B
C
D
D’
A’
K0
•
4
2
1 1 1 1
(x a) (x a) a 4 =2 2 (3)
2 2 (x a) a 4
− + − + + ≥
−
•Do đó (1) ch đúng khi d u đ ng th c x y ra t i (3) t c là:ỉ ấ ẳ ứ ả ạ ứ
2
3 2
x
1 1 2
(x a) a
2 (x a) a 2
a2
=
− = = ⇔
−=
•V y h có nghi m khi và ch khi a = ậ ệ ệ ỉ
2
2
và nghi m c a h là: x = ệ ủ ệ
3 2
2
.