PHÒNG GD&ĐT THANH
OAI
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 NĂM HỌC 2013 - 2014
Môn:
Toán
Thời gian: 150 phút (không kể thời gian giao đề)
Đề thi gồm có: 01 trang
Câu 1: (6 điểm)
a) Cho
)
65
2
3
2
2
3
(:)
1
1(
xx
x
x
x
x
x
x
x
M
1. Rút gọn M
2. Tìm giá trị nguyên của x để biểu thức M nhận giá trị là số nguyên
b) Tính giá trị của biểu thức P
200653 20112013 xxP
với
328183223.226 x
Câu 2: (4 điểm) Giải phương trình
a) (
24)6)(5)(4)(3 xxxx
b) |
| =
12 2 xx
Câu 3: (4 điểm)
a/ Cho hai số dương x, y thoả mãn x + y = 1.
Tìm giá trị nhỏ nhất của biểu thức:
22
22
11
M x y
yx






b/ Cho x, y, z là các số dương thoả mãn
1 1 1 6
x y y z z x

.
Chứng minh rằng:
1 1 1 3
3 3 2 3 2 3 2 3 3 2x y z x y z x y z
.
Câu 4: (5 điểm)
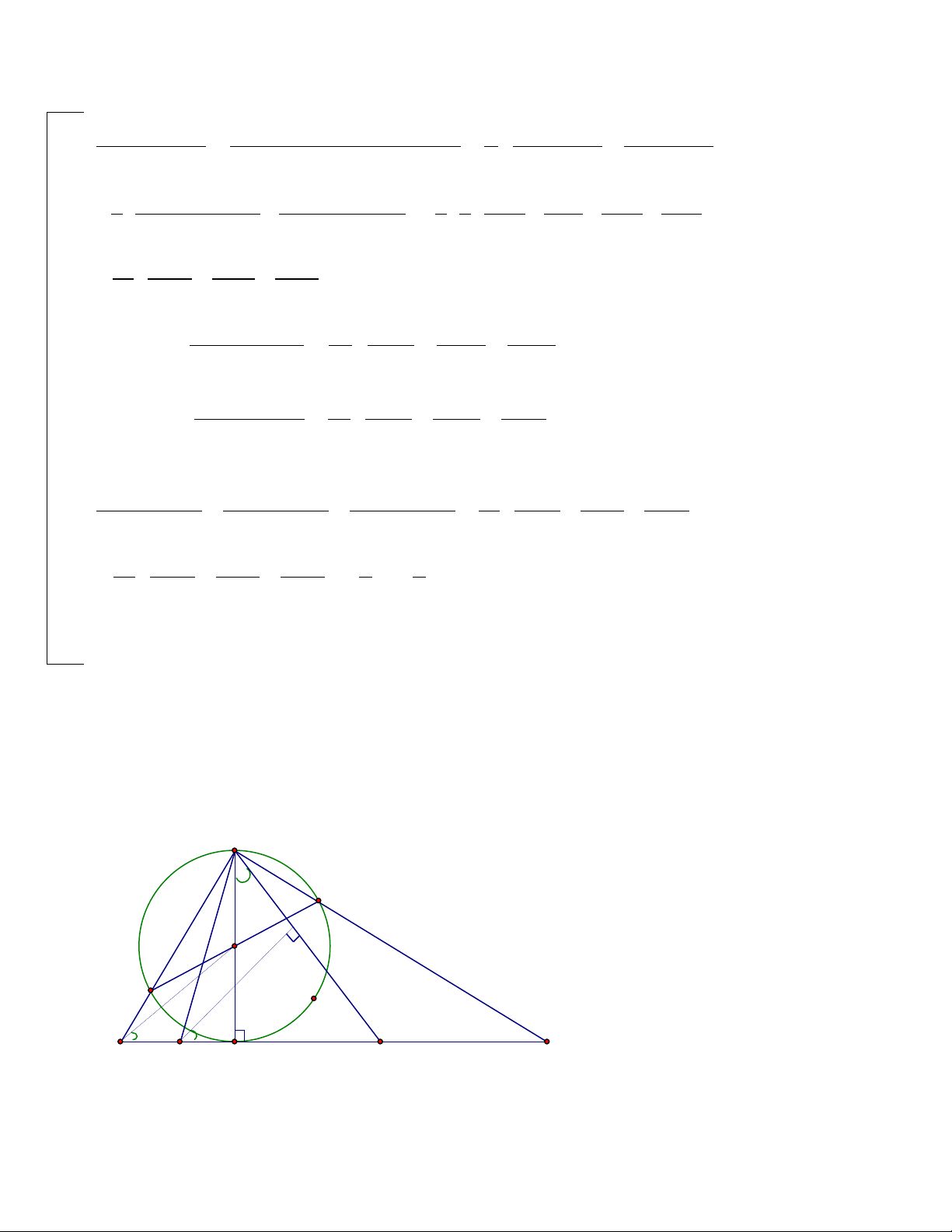
Cho đường tròn (O; R) và hai đường kính AB và CD sao cho tiếp tuyến tại A của
đường tròn (O; R) cắt các đường thẳng BC và BD tại hai điểm tương ứng là E và F.
Gọi P và Q lần lượt là trung điểm của các đoạn thẳng AE và AF.
1. Chứng minh rằng trực tâm H của tam giác BPQ là trung điểm của đoạn thẳng OA.
2. Gọi α là số đo của góc BFE. Hai đường kính AB và CD thoả mãn điều kiện gì
thì biểu thức
66
sin cosP


. Đạt giá trị nhỏ nhất? tìm giá trị nhỏ nhất đó.
3. Chứng minh các hệ thức sau: CE.DF.EF = CD3 và
3
3
BE CE
BF DF
.
Câu 5: (1 điểm)
Tìm n
N*sao cho: n4 +n3+1 là số chính phương.
PHÒNG GD&ĐT THANH
OAI
HƯỚNG DẪN CHẤM THI CHỌN HỌC SINH GIỎI LỚP 9
NĂM HỌC 2013 - 2014
Môn:
Toán
Câu 1: (6 điểm)
a) (4,5đ)
ĐKXĐ:
9;4;0 xxx
(*)
1)Rút gọn M : Với
9;4;0 xxx
(0,5đ)
1
2
)3)(2(
2)4(9
:
1
1
)3)(2(
)2()2)(2()3)(3(
:
1
1
)3)(2(
2
3
2
2
3
:
1
1
x
x
xx
xxx
x
xx
xxxxx
x
xx
x
x
x
x
x
x
xx
M
Vậy
1
2
x
x
M
(với
9;4;0 xxx
) (*) (2,5đ)
2)
1
3
1
1
3
1
1
1
31
1
2
xxx
x
x
x
x
x
M
(0,75đ)
Biểu thức M có giá trị nguyên khi và chỉ khi:
)3(113 Uxx
Ư(3)
3;1
Vì
0 0 1 1x x x
Nên
3;11x
Xảy ra các trường hợp sau: (0,5đ)
.
0011 xxx
(TMĐK (*) )
.
4231 xxx
(không TMĐK (*) loại ) (0,25đ)
Vậy x = 0 thì M nhận giá trị nguyên.
b_
3.28183223.226 x
Có
2424)24(2818 2
(0,5đ)
13)13(43224322 2
(0,25đ)
6 2 2. 3 3 1 3 6 2 2. 2 3 3 6 2 4 2 3 3x
3324313263)13(26 2x
13133133)13( 2x
(0,75đ)
Với x = 1.Ta có
201420065320061.51.3 20112013 P
Vậy với x = 1 thì P = 2014
Câu 2: (4 điểm)
a. (
24)5)(4)(6)(3 xxxx
24)209)(189( 22 xxxx
(1)
Đặt
yxx 199
2
(1) ( y + 1)(y – 1 ) – 24 = 0
y2 – 25 = 0
0)149)(249( 22 xxxx
0)249)(7)(2( 2 xxxx
Chứng tỏ
0249
2 xx
Vậy nghiệm của phương trình :
7;2 xx
b. Ta có
0)1()12(12 222 xxxxx
pt trở thành :
1212 22 xxxx
1x
0,25 đ
0,25 đ
0,5 đ
0,5 đ
0,25 đ
0,5 đ
0,5 đ
0,25 đ
0,25 đ
0,5 đ
0,25 đ
Câu 3: (4 điểm)
a
Cho hai số dương thỏa mãn: x + y =1.
Tìm GTNN của biểu thức: M =
22
22
11
xy
yx







M =
22
22
11
xy
yx







=
4 4 2 2
22
2 2 2 2
1 2 1
11 x y x y
xy x y x y

2đ
222
22 22
22
111
xy xy xy
x y xy xy






Ta có:
1 1 15
16 16
xy xy
xy xy xy



* Ta có:
1 1 1 1
2 . 2.
16 16 4 2
xy xy
xy xy
(1) *
1 1 1 1 4 1 15 15
4
2 2 4 16 16 4 16 4
xy
xy xy xy xy xy
(2)
Từ (1) và (2)
1 1 15 1 15 17
16 16 2 4 4
xy xy
xy xy xy
Vậy M =
22
1 17 289
4 16
xy xy






Dấu “=” xảy ra
111
16 42
xy xy
xy xy
xy
xy



(Vì x, y > 0)
Vậy min M =
289
16
tại x = y =
1
2
0,5
0, 5
0,5
0,25
0,25
0,5
b
Cho x, y là các số dương thỏa mãn:
1 1 1 6
x y y z z x

Chứng minh rằng:
1 1 1 3
3 3 2 3 2 3 2 3 3 2x y z x y z x y z
2đ
Áp dụng BĐT
1 1 4
a b a b

(với a, b > 0)
1 1 1 1
4a b a b



Ta có:
0.5
1 1 1 1 1
3 3 2 2 2 4 2 2x y z x y z x y z x y z x y z



1 1 1 1 1 1 1 1 1
4 4 4x y x z x y y z x y x z x y y z










1 2 1 1
16 x y x z y z



Tương tự:
1 1 2 1 1
3 2 3 16x y z x z x y y z



1 1 2 1 1
2 3 3 16x y z y z x y x z



cộng vế theo vế, ta có:
1 1 1 1 4 4 4
3 3 2 3 2 3 2 3 3 16x y z x y z x y z x y x z y z



4 1 1 1 1 3
.6
16 4 2x y x z y z



0,5
0,5
0,5
0,5
Caai 4: (5 điểm)
0,25
.
1
1
I
H
Q
P
O
A
F
D
C
E
B