Đ KIM TRA HKI – NĂM HC 2017 – 2018
Môn: TON 10 – Thi gian: 90 pht
Đ CHẴN
Bài 1: (1 điểm) Cho hàm số
2
( ) 2 3y f x x x
. Khảo sát và vẽ đồ thị (P) của hàm số
Bài 2: (2 điểm) Cho phương trình
26 2 0x m x m
. Định m để :
a. Phương trình có một nghiệm.
b.Phương trình có hai nghiệm
12
,xx
thỏa
33
1 2 1 2 0x x x x
Bài 3: (2 điểm) Giải hệ phương trình và bất phương trình sau:
a)
34
34
y
xy x
x
yx y


b)
2
12 2x 4x 3
3x 2
x
Bài 4: (2 điểm) Trong hệ trục Oxy, lấy ba điểm A(1;2), điểm B(-1;1) và điểm C(3;-2).
a) Tính
.AB CA
uuur uuur
. Từ đó suy ra hình tính tam giác và tính diện tích tam giác ABC
b) Xác định tọa độ chân đường cao hạ từ A xuống BC.
Bài 5: (2 điểm) Cho tam giác ABC có AB = 14, góc A = 60o, góc B = 450. Tính độ dài cạnh BC,
bán kính đường tròn ngoại tiếp và diện tích tam giác ABC. (Các kết quả có thể để dưới dạng số
thập phân , làm tròn hai số sau dấu phẩy)
Bài 6: (1 điểm) David Beckham là cầu thủ người Anh và là chuyên gia sút phạt hàng đầu của
bóng đá thế giới. Những cú sút phạt của anh thường đi theo hình vòng cung, gây rất nhiều khó
chịu cho các thủ môn. Giả sử như trong một lần sút phạt, kỹ thuật máy tính chỉ ra rằng cú sút
phạt của Beckham đi theo quỹ đạo là một đường cong Parabol có phương trình
2
0,0083x 0,1x 2,7hx
với h(x) là độ cao (m) của quả bóng so với mặt đất tại nơi cách
vạch vôi khung thành một khoảng cách x (m) (xem hình ảnh minh họa).
(hình ảnh thể hiện cách đặt trục, không có tính kết luận về kết quả bài toán )
a) Lúc đó, Beckham đang đặt trái bóng tại điểm cách vạch vôi khung thành bao nhiêu
mét?
b) Khi sút phạt, đội bạn sẽ cử 4 đến 5 người làm “hàng rào” để chắn bóng, “hàng rào”
nằm giữa khung thành và điểm sút phạt và cách điểm sút theo quy định là 9,15 m. Hỏi quả bóng
sút theo quỹ đạo này có vượt qua được “hàng rào” không và cú sút phạt của Beckham có đưa
được bóng vào phạm vi của khung thành không? Biết rằng, cầu thủ đội bạn chỉ nhảy cao được tối
đa 2m để chắn bóng và khung thành có chiều cao 2,4 m (theo chuẩn quốc tế)
(Các kết quả có thể để dưới dạng số thập phân , làm tròn hai số sau dấu phẩy)
Đ KIM TRA HKI – NĂM HC 2017 – 2018
Môn: TON 10 – Thi gian: 90 pht
Đ LẺ
Bài 1: (2 điểm) Cho hàm số
. Khảo sát và vẽ đồ thị (P) của hàm số
Bài 2: (2 điểm) Cho phương trình
25 3 0x m x m
. Định m để :
a. Phương trình có một nghiệm.
b. Phương trình có hai nghiệm
12
,xx
thỏa
33
1 2 1 2 0x x x x
Bài 3: (2 điểm) Giải hệ phương trình và bất phương trình sau:
a)
34
34
y
xy x
x
yx y
b)
2
12 2x 4x 3
3x 2
x
Bài 4: (2 điểm) Trong hệ trục Oxy, lấy ba điểm M(1;2), điểm N(-1;1) và điểm P(3;-2).
a) Tính
.MN PM
uuuur uuuur
. Từ đó suy ra hình tính tam giác và tính diện tích tam giác MNP
b) Xác định tọa độ chân đường cao hạ từ M xuống NP.
Bài 5: (2 điểm) Cho tam giác ABC có BC = 16, góc B = 45o, góc C = 300. Tính độ dài cạnh AB,
bán kính đường tròn ngoại tiếp và diện tích tam giác ABC. (Các kết quả có thể để dưới dạng số
thập phân , làm tròn hai số sau dấu phẩy)
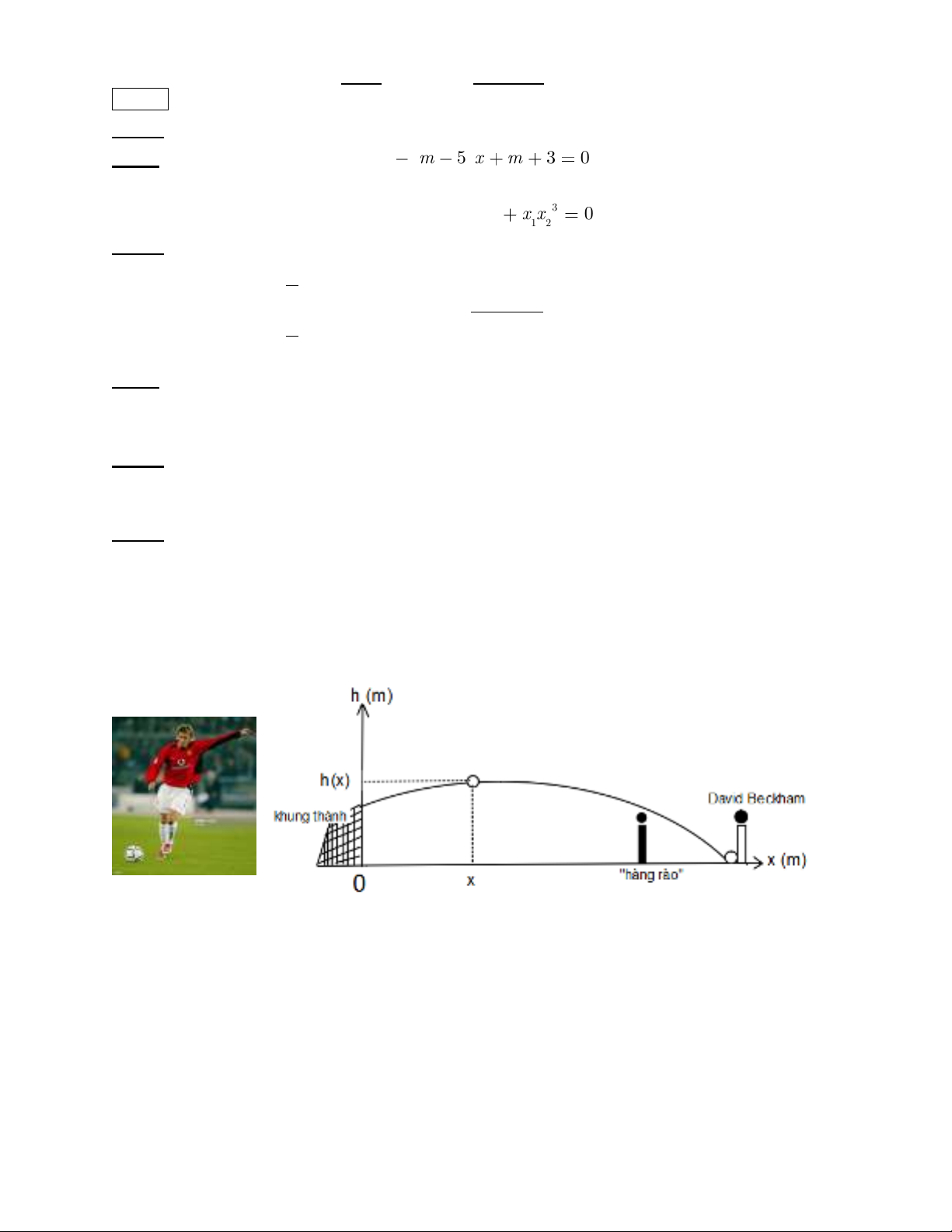
Bài 6: (1 điểm) David Beckham là cầu thủ người Anh và là chuyên gia sút phạt hàng đầu của
bóng đá thế giới. Những cú sút phạt của anh thường đi theo hình vòng cung, gây rất nhiều khó
chịu cho các thủ môn. Giả sử như trong một lần sút phạt, kỹ thuật máy tính chỉ ra rằng cú sút
phạt của Beckham đi theo quỹ đạo là một đường cong Parabol có phương trình
2
0,0083x 0,1x 2,7hx
với h(x) là độ cao (m) của quả bóng so với mặt đất tại nơi cách
vạch vôi khung thành một khoảng cách x (m) (xem hình ảnh minh họa).
(hình ảnh thể hiện cách đặt trục, không có tính kết luận về kết quả bài toán )
a) Lúc đó, Beckham đang đặt trái bóng tại điểm cách vạch vôi khung thành bao nhiêu
mét?
b) Khi sút phạt, đội bạn sẽ cử 4 đến 5 người làm “hàng rào” để chắn bóng, “hàng rào”
nằm giữa khung thành và điểm sút phạt và cách điểm sút theo quy định là 9,15 m. Hỏi quả bóng
sút theo quỹ đạo này có vượt qua được “hàng rào” không và cú sút phạt của Beckham có đưa
được bóng vào phạm vi của khung thành không? Biết rằng, cầu thủ đội bạn chỉ nhảy cao được tối
đa 2m để chắn bóng và khung thành có chiều cao 2,4 m (theo chuẩn quốc tế)
(Các kết quả có thể để dưới dạng số thập phân , làm tròn hai số sau dấu phẩy
THANG ĐIM VÀ ĐP N
Đề chẵn
Điểm
Để lẻ
Bài 1
2
( ) 2 3y f x x x
TXD: D = R
BBT:
BGT
Vẽ đồ thị
Đỉnh: I ( 1; -2)
Trục đối xứng x = 1
Bài 1
TXD: D = R
BBT:
BGT
Vẽ đồ thị
Đỉnh: I ( 1; 2)
Trục đối xứng x = 1
Bài 2:
26 2 0x m x m
a)
216 28mm
Để phương trình có nghiệm kép
1 0( )
0 14
14
02
2
LD
am
mm
m





b)
Phương trình có hai nghiệm:
2
0 16 28 0mm
Theo hệ thức Viete
12
12
6
.2
b
S x x m
a
c
P x x m
a
Theo đề, ta có:
33
1 2 1 2
2
2
2
0
20
0
20
20
14 32 0
2
7 17
7 17
x x x x
P S P
P
SP
m
mm
mN
mL
mL
Vậy m = -2 thỏa ycđb
Bài 2:
25 3 0x m x m
a)
214 13mm
Để phương trình có nghiệm kép
1 0( )
0 13
13
01
1
LD
am
mm
m





b)
Phương trình có hai nghiệm:
2
0 14 13 0mm
Theo hệ thức Viete
12
12
5
.3
b
S x x m
a
c
P x x m
a
Theo đề, ta có:
33
1 2 1 2
2
2
2
0
20
0
20
30
12 19 0
3
6 17
6 17
x x x x
P S P
P
SP
m
mm
mN
mL
mL
Vậy m = -3 thỏa ycđb
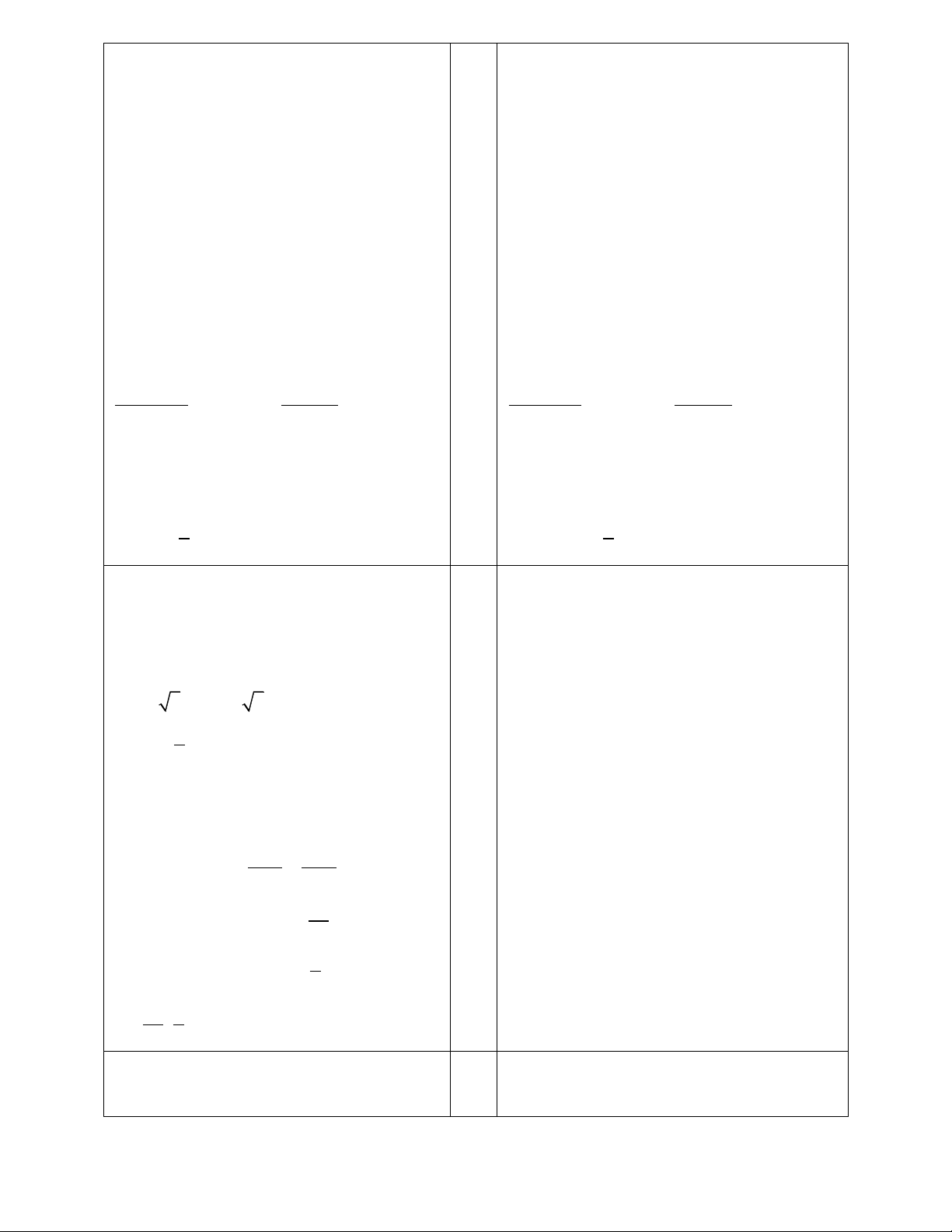
Bài 3:
a)
Bài 3:
a)
2
2
2
2
3 4 1 : 0; 0
3x 4x 2
1 2 4 0
1:
1 2x 4x 0
0
2
2 : 4
2 4 4 0 2 2
2; 2
x xy y Dk x y
yy
x y x y
TH x y
x y L
x y N
TH x y
y y y x
hpt co nghiem





b)
2
12 2x 3x 6
4x 3 0
3x 2 3x 2
x

Kẻ bảng xét dấu
KL:
2;2
3
S

2
2
2
2
3 4 1 : 0; 0
3 4 2
1 2 4 0
1:
1 4x 4x 0
0
1
2 : 4
2 4 8 0
1; 1
x yx y Dk x y
y xy x
x y x y
TH x y
x y L
x y N
TH x y
y y ptvn
hpt co nghiem




b)
2
12 2x 3x 6
4x 3 0
3x 2 3x 2
x

Kẻ bảng xét dấu
KL:
2
; 2;
3
S
 


Bài 4:
a) A(1;2), điểm B(-1;1) và điểm C(3;-2)
2; 1 ; 2;4
.0
AB CA
AB CA
uuur uuur
uuur uuur
Suy ra tam giác ABC vuông tại A
5;AC 2 5
1.5
2
ABC
AB
S AB AC


V
b) Gọi H(x; y) là chân đường cao hạ từ A xuống
BC ta có hpt:
4 1 3 2 0
.0
11
,43
1
4x 3 2 5
3x+4 1 2
5
12
;
55
xy
AH BC
xy
BH BC cp
x
y
yy
H








uuur uuur
uuur uuur
Kết quả giống đề chẵn
Bài 5: AB = 14, góc A = 60o, góc B = 450.
Tính độ dài cạnh BC, bán kính đường tròn
ngoại tiếp và diện tích tam giác ABC.
Bài 5: BC = 16, góc B = 45o, góc C = 300.
Tính độ dài cạnh AB, bán kính đường tròn
ngoại tiếp và diện tích tam giác ABC.
0 0 0 0
180 60 45 75
sin 60
14. 12,55
sin sin sin 75
14 7.25
2sin 2sin 75
1
S . .sin
2
1.14.12,55.sin 45 62.12
2
C
BC AB BC
AC
AB
RC
AB BC B
S

0 0 0 0
180 30 45 105
sin 30
16. 11,31
sin sin sin105
16 8, 28
2sin 2sin105
1
S . .sin
2
1.16.11,31.sin 45 63.4
2
A
BC AB BA
AC
BC
RA
AB BC B
S

Bài 6:
2
0,0083x 0,1x 2,7hx
a)
2
0
0,0083x 0,1x 2, 7 0
13
25
hx
xL
xN

Vậy quả bóng được đặt cách vạch vôi khung thành 25 mét
b)
Khoảng cách từ vạch vôi đến “hàng rào”: 25 – 9.15 = 15.85 (m)
Tại x = 15.85 độ cao quả bóng là:
15.85 2,2hm
. Vậy bóng bay qua được “hàng rào”
Cho x = 0 độ cao quả bóng là
0 2,7hm
. Vậy quả bóng đã bay cao hơn khung thành (2,4 m) nên
bóng không thể bay vào phạm vi khung thành được