Đề thi học kì 1 môn Toán lớp 9 năm 2022-2023 có đáp án - Trường THCS Việt Nam-Angiêri

Chia sẻ: _ _ | Ngày: | Loại File: DOCX | Số trang:9

Thêm vào BST

Báo xấu

21
lượt xem 1
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

“Đề thi học kì 1 môn Toán lớp 9 năm 2022-2023 có đáp án - Trường THCS Việt Nam-Angiêri” giúp các bạn học sinh có thêm tài liệu ôn tập, luyện tập giải đề nhằm nắm vững được những kiến thức, kĩ năng cơ bản, đồng thời vận dụng kiến thức để giải các bài tập một cách thuận lợi. Chúc các bạn thi tốt!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề thi học kì 1 môn Toán lớp 9 năm 2022-2023 có đáp án - Trường THCS Việt Nam-Angiêri

PHÒNG GD&ĐT QUẬN THANH XUÂN ĐỀ KIỂM TRA HỌC KÌ I Môn: TOÁN 9 Thời gian làm bài : 90 phút Bài I.( 2,0 điểm) 1) Tính giá trị của biểu thức: 2) Giải phương trình: Bài II. (2 điểm) Cho biểu thức: A=; B= ĐK: x>0 ; x≠9 1) Tính giá trị của biểu thức A khi x=36. 2) Chứng tỏ B=. 3) Cho P=A.B, tìm x là số nguyên tố để P có giá trị âm. Bài III. (2,5 điểm) 1. Cho hàm số bậc nhất : y=(m+1)x+m-3 có đồ thị là đường thẳng d ( m là tham số). a) Tìm m để đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 2. b) Tìm m để đường thẳng (d) cắt trục Ox, Oy lần lượt tại A và B sao cho tam giác AOB vuông cân. 2. Một chiếc máy bay bay lên với vận tốc 400km/h . Đường bay lên tạo với phương nằm ngang một góc 300 . Hỏi sau 1,5 phút máy bay ở độ cao bao nhiêu km so với mặt đất ? Giả sử mặt đất bằng phẳng và vận tốc máy bay không đổi. 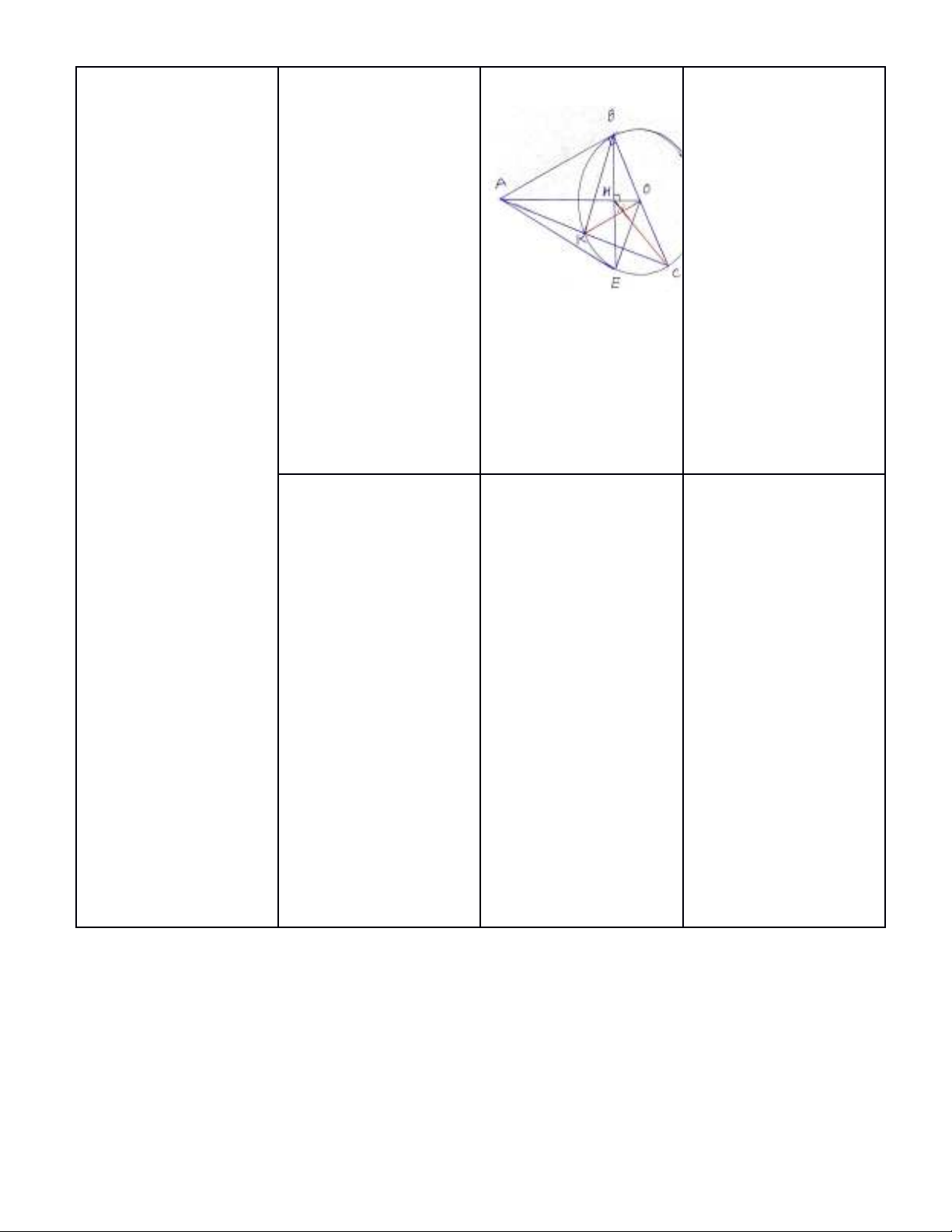Bài IV. (3 điểm) Cho đường tròn (O;R) lấy điểm A ở bên ngoài đường tròn, kẻ tiếp tuyến AB và đường kính BC. Kẻ dây BE vuông góc với AO tại H 1) Chứng minh: OH.OA =R2 2) Chứng minh: AE là tiếp tuyến của đường tròn tâm O và 4 điểm A,B,E,O cùng thuộc một đường tròn. 3) Gọi đoạn AC cắt (O) tại điểm tại K, chứng minh : Bài V. (0,5 điểm) Cho x,y,z>0 và x+y+z=1. Tìm giá trị nhỏ nhất của P=
ĐÁP ÁN VÀ THANG ĐIỂM MÔN TOÁN 9 Bài Ý Đáp án Điểm 1 = 1 Bài I 2 điểm ĐK: x≥-3 0,5 đ Vậy tập nghiệm của phương trình là : S={- 2 11/25} 0,5 đ
1 x=36(tmđk) thay vào A 0,5 đ Bài II ta được A=2/3. Vậy x= 2 điểm 365 thì A=2/3 B= = 0,5 đ 2 0,5 đ Ta có P=A.B=.....= mà 0,25đ 3 P có giá trị âm=> P x +3 ≥3>0 0,25đ 
y=(m+1)x+m-3 (d) ĐK: 0,25đ m≠-1. 1a Vì đường thẳng (d) cắt Bài III trục tung tại điểm có 0,5đ 2,5 điểm tung độ 2 suy  m-3=2  m=5(tmđk) Vậy m=5 thì đường thẳng (d) cắt trục tung tại điểm có tung độ 2 ĐK: m≠-1. y=(m+1)x+m-3 Cho x=0=>y=m-3 suy ra B(0;m-3) €Oy=> OB=| m-3| (đvđ d) 0,25đ 1b Cho x=0 suy ra (m+1)x+m-3=0=> => ;0) €Ox A(  OA=(đvđ d) Vì ∆ABO vuông cân ở O  OA=OB =|m-3|  .....  Vậy m€{-2;0;3} 0,5đ thì đường thẳng (d) cắt Ox, Oy tại A và B mà ∆ABO vuông cân 2 Gọi AC là đoạn đường máy bay bay lên trong 0,5đ 1,5 phút, CB là độ cao máy bay đạt được sau 1,5 phút 0,5đ Theo đề bài ta có góc BAC =300 Đổi 1,5 phút =1/40h. Độ dài AC là: 400.1/40=10km Xét ∆ABC vuông ở B ta có BC=AC. sin A=> BC= 10.0,5=5km Vậy sau 1,5 phút máy bay bay lên cao được 5km.
0,25đ 1 Bài IV 3 điểm 0,5đ 0,5đ Xét đường (O) có AB là tiếp tuyến (gt) suy ra góc ABO = 900 ∆ABO vuông tại B Xét đường cao BH có OH.OA=OB2(htl...) mà OB=R => OH.OA=R2 Ta có OB=OE=R => ∆BOE cân ở O mà OH 2 là..... => góc BOA= góc EOA C/minh ∆AOB=∆AOE 0,5đ (cgc) suy ra góc AEO=góc ABO mà góc ABO=900 (cmt) => góc AEO=900 => AE EO tại 0,5đ E mà OE là bán kính của đường tròn (O) => AE là tiếp tuyến của (O) +) ∆AOB vuông ở B=> 3 điểm A,B,O thuộc đường tròn đường kính AO (1) +) ∆AOE vuông ở E=> 3 điểm A,E,O thuộc đường tròn đường kính AO (2). Từ (1) và (2) suy ra 4 điểm A,B, O, E cùng thuộc đường tròn đường kính AO.
∆ABO vuông tại B Xét đường cao BH có 3 AH.AO=AB2(htl...)(3) +) Ta có ∆BKC nội tiếp 0,5đ đường tròn (O) mà cạnh BC là đường kính suy ra ∆BKC vuông ở K suy ra BK vuông góc AC. 0,25đ ∆ABC vuông tại B Xét đường cao BKcó AK.AC=AB2(htl...)(4) Từ (3); (4) suy ra AH.AO= AK.AC => AK/AO=AH/AC +) Xét ∆AKO và ∆AHC ta có góc KAH chung và AK/AO=AH/AC (cmt) Suy ra ∆AKO đồng dạng ∆AHC (cgc) suy ra góc AOK = góc ACH ( 2 góc tương ứng ). Ta có 4(2x2+xy+2y2)=5(x+y)2+ 3(x-y)2 ≥5(x+y)2 Bài V 0,25đ 0,5 điểm và CMTT ta có: => Suy ra Dấu “ = “ xảy ra khi 0,25đ x=y=z=1/3 Vậy P min = khi x=y=z=1/3
Chú ý : các cách khác làm đúng vẫn cho điểm tối đa
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I MÔN : TOÁN 9 CẤP VẬN DỤNG CỘNG ĐỘ NHẬN THÔNG HIỂU CẤP ĐỘ CẤP ĐỘ BIẾT THẤP CAO CHỦ ĐỀ Chủ đề 1: Tính giá trị Cộng trừ căn biểu thức bậc hai Tính giá trị biểu thức Số câu 1 1 2 Số điểm 0,5 1 1,5 Tỷ lệ 5% 10% 5% Chủ đề 2: Rút gọn biểu Rút gọn biểu thức thức chứa căn Số câu 1 1 Số điểm 1 1 Tỷ lệ 10% 10% Chủ đề 3: Giải phương trình Biến đổi Giải bất Tìm giá trị và bất phương căn thức phương trình nhỏ nhất trình Số câu 1 1 1 3 Số điểm 1 0,5 0,5 2 Tỷ lệ 10% 5% 5% 20% Chủ đề 4: Tính số đo Cách CM Tỉ số lượng giác- góc vuông góc HTL Số câu 1 1 2
Số điểm 1 0,5 1,5 Tỷ lệ 10% 5% 15% Chủ đề 5: CM điểm Chứng Nhận biết Chứng minh Tiếp tuyến của thuộc minh góc tiếp tuyến tiếp tuyến đường tròn đường tròn bằng nhau Số câu 1 1 1 1 2 Số điểm 1 0,5 0,75 0,5 2,5 Tỷ lệ 7,5% 5% 7,5% 5% 15% Chủ đề 6: Nhận biết Tính độ dài điểm thuộc Đồ thị hàm số đoạn thẳng ĐT Số câu 1 1 2 Số điểm 0,75 0,75 1, 5 Tỷ lệ 7,5% 7,5% 15% Tổng số câu 4 2 6 2 17 Tổng số điểm 3 1,5 4,5 1 10 Tỷ lệ 30% 15% 45% 10% 100 %