ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG NĂM HỌC 2009 - 2010
Huỳnh Kim Linh Sưu tầm và giới thiệu
——————
Bài 1 :
Cho a, b, c ∈(0; 1). Chứng minh rằng :√abc +q(1 −a) (1 −b) (1 −c)<1.
Bài 2 :
Cho các số thực x, y, z khác không. Tìm tất cả giá trị của :
f(x, y, z) = |x+y|
|x|+|y|+|y+z|
|y|+|z|+|z+x|
|z|+|x|.
Bài 3 :
Cho n là số tự nhiên lẻ và tập các số thực X={x1;x2;. . . ;xn}.
Tìm tất cả các song ánh f (hàm 1-1) trên tập X, f:X→X
sao cho :
|f(x1)−x1|=|f(x2)−x2|=··· =|f(xn)−xn|.
Bài 4 :
Cho 7 số thực thuộc khoảng (1; 13). Chứng minh rằng có ít nhất ba số trong đó là độ dài 3 cạnh của
1 tam giác.
Bài 5 :
Cho a, b, c > 0. Giải hệ phương trình :
ax −by +1
xy =c
bz −cx +1
zx =a
cy −az +1
yz =b.
Bài 6 :
Cho hình vuông ABCD có cạnh bằng 1 và bên trong hình vuông cho n điểm phân biệt. Chứng minh
rằng tồn tại một tam giác có đỉnh tại các điểm đã cho hoặc là đỉnh của hình vuông sao cho diện tích
S của nó thỏa mãn bất đẳng thức :
S≤1
2(n+1) .
——— HẾT ———
SỞ GIÁO DỤ C VÀ ĐÀO TẠ O GIA LAI KÌ THI CHỌ N HỌ C SINH GIỎ I CẤ P TRƯ Ờ NG
TRƯ Ờ NG THPT HUỲNH THÚC KHÁNG NĂM HỌ C 2009 – 2010
------------------------------------------ MÔN THI: TOÁN
ĐỀ CHÍNH THỨ C Thờ i gian: 180 phút (Không kể thờ i gian phát đề )
ĐỀ BÀI
Câu 1. (5.0 điể m)
a) Giả i hệ phư ơ ng trình:
2
2
2 4 4
2
2 4 4
2
log ( 4 5) 1 2
log ( 4 5) 1 2
y y
x x
x x
y y
b) Giả i phư ơ ng trình:
2 3 3 2
1 1 (1 ) (1 ) 2 1x x x x
Câu 2. (4.0 điể m)
Cho dãy số
n
x
đư ợ c xác đị nh bở i
0
2 2
1
1
0
2010
2 , , 1
n
n
n
x m m
x
x n n
x
.
Tìm
lim n
nx

Câu 3. (3.0 điể m)
Giả sử a, b,c là các số không âm. Chứ ng minh rằ ng
Câu 4. (3.0 điể m)
Cho
( )f x
là hàm số đồ ng biế n và là hàm số lẻ trên
. Giả sử a, b, c là ba số thự c thỏ a
mãn:
0abc
. Chứ ng minh rằ ng
( ) ( ) ( ) ( ) ( ) ( ) 0f a f b f b f c f c f a
.
Câu 5. (6.0 điể m)
1. Trong mặ t phẳ ng tọ a độ Oxy cho đư ờ ng tròn (C) có phư ơ ng trình
2 2
( 1) 1x y
Chứ ng minh rằ ng vớ i mỗ i điể m
( ;3)M m
trên đư ờ ng thẳ ng y = 3 ta luôn tìm đư ợ c hai
điể m T1, T2 trên trụ c hoành, sao cho các đư ờ ng thẳ ng
1 2
,MT MT
là tiế p tuyế n củ a (C).
Khi đó hãy viế t phư ơ ng trình đư ờ ng tròn ngoạ i tiế p tam giác MT1T2.
2. Cho tam giác đề u ABC có cạ nh a, ngư ờ i ta đặ t vào đó 5 điể m bấ t kì. Chứ ng minh
rằ ng luôn tồ n tạ i mộ t cặ p điể m mà khoả ng cách giữ a chúng nhỏ hơ n hoặ c bằ ng
2
a
.
------------------------------HẾ T-------------------------------
HƯ Ớ NG DẪ N CHẤ M ĐIỂ M KÌ THI HỌ C SINH GIỎ I CẤ P TRƯ Ờ NG
NĂM HỌ C 2008 – 2009
Bài
Đáp án
Điể m
1
a
Đặ t
2 2
4 4, v = y 4 4 (u,v 0)u x x y
Hệ phư ơ ng trình trở thành:
2
2
log ( 1) 1 2 (I)
log ( 1) 1 2
v
u
u
v
Giả sử (u0 ; v0) là mộ t nghiệ m củ a hệ (I).
Nhậ n xét, nế u
0 0 2 0 2 0
log ( 1) log ( 1)u v u v
0 0 0 0 0 0
2 2
v u v u u v
Tư ơ ng tự
0 0 0 0 0 0
u v v u u v
Do đó: (I)
2
2
log ( 1) 1 2
log ( 1) 1 2
u
v
u
v
u v
Đặ t
2
( ) 2 log ( 1) 1, D=[0;+ )
t
f t t
1
'( ) 2 ln 2 ( 1)ln 2
t
f t t
2
2
1
"( ) 2 ln 2 0 D
( 1) ln 2
t
f t t
t
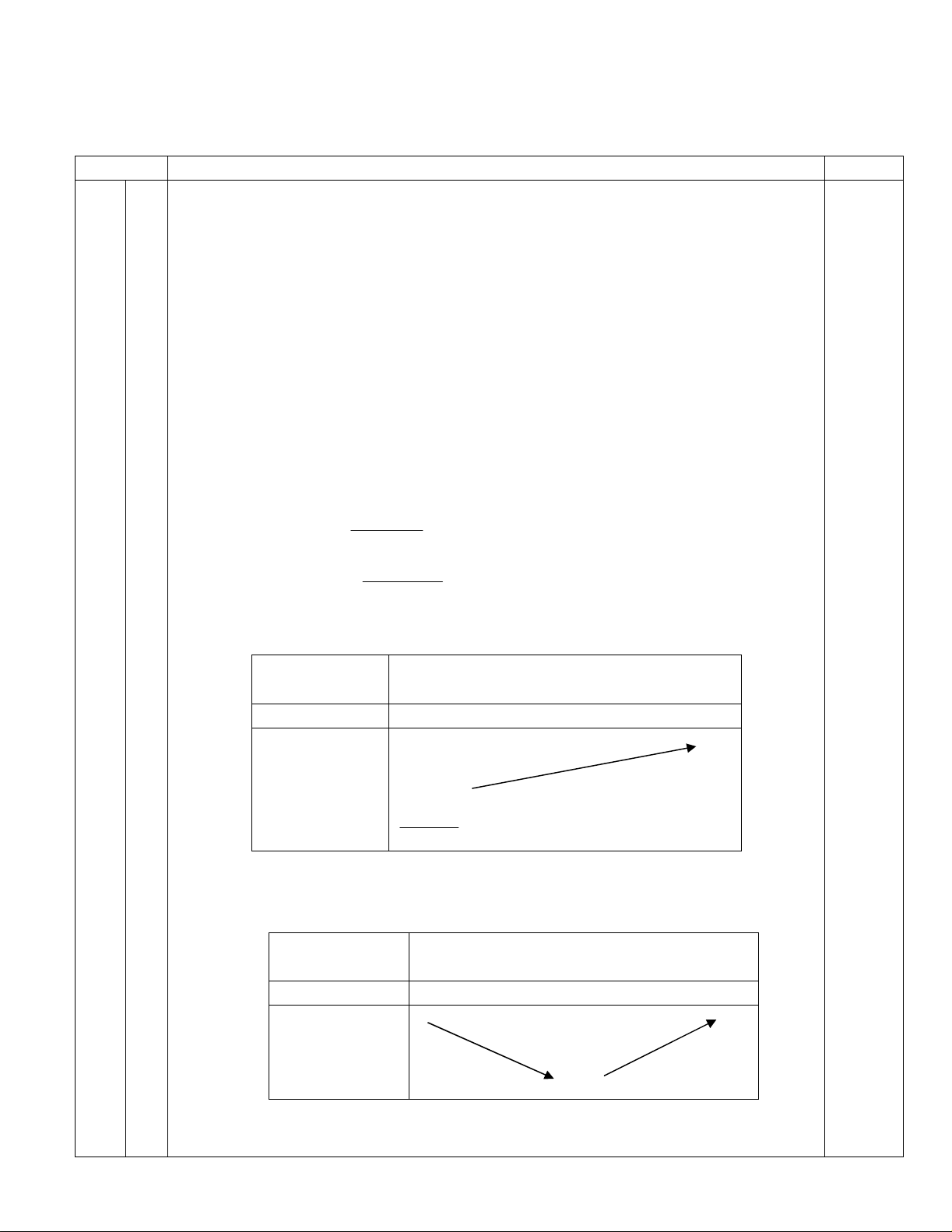
Ta lậ p bả ng biế n thiên củ a f’(x):
t
0
+
f”(t)
+
f'(t)
+
2
ln 2 1
ln 2
Suy ra phư ơ ng trình f’(t) = 0 có nghiệ m duy nhấ t t = a.
Ta lậ p đư ợ c bả ng biế n thiên củ a f(t)
t
0 a
+
f'(t)
- 0 +
f(t)
f(a)
Suy ra phư ơ ng trình
2
( ) 2 log ( 1) 1 0
t
f t t
(1) có nhiề u nhấ t hai nghiệ m
0.5
0.5
0.5
0.5
0.5
Mặ t khác, ta nhậ n thấ y t = 0, t = 1 là nghiệ m củ a phư ơ ng trình (1).
Vậ y phư ơ ng trình (1) có đúng hai nghiệ m là t = 0, t = 1.
Suy ra hệ (I) có hai nghiệ m là (0;0) và (1;1)
Suy ra hệ phư ơ ng trình đã cho có 5 nghiệ m: (2; 2), (1; 1), (3; 3), (1; 3), (3; 1)
0.5
b
ĐK:
1 1x
.
Nhậ n xét, nế u
1 0x
thì
3 3
(1 ) (1 ) 0x x
, suy ra phư ơ ng trình đã cho
vô nghiệ m. Do đó
0 1x
. Đặ t
os , 0; 2
x c t t
Khi đó phư ơ ng trình đã cho trở thành
1
2 2 ost 1 sin 2 sin
2
c t t
2
2 sin 2 cos 1 0 cos 2
t t t
Vậ y phư ơ ng trình có mộ t nghiệ m
2
2
x
0.5
0.5
1.0
2
+Từ giả thiế t, ta có :
2
1
1
1 2010
2
n n
n
x x x
Suy ra :
2
0
0
1
2
1
0
0
1 2010 2010
2
2010
2010 1 2010 2010
2
xx
x
xxx
=
1
2
2 2 1
0 0
2
2 2
0 0 1
2
2010
2.2010. 2010 2010
2.2010. 2010 2010
2010
x
x x m
x x m
x
Dự đoán :
2010
2010
n
n
x
x
=
2
2010
2010
n
m
m
Chứ ng minh bằ ng qui nạ p :
n = 1 , mệ nh đề đúng.
Giả sử mệ nh đề đúng vớ i n=k . Ta có
2010
2010
k
k
x
x
=
2
2010
2010
k
m
m
Ta cầ n chứ ng minh mệ nh đề đúng vớ i n=k+1, thậ t vậ y
1
1
2010
2010
k
k
x
x
=
2
2
1 2010 2010
2
1 2010 2010
2
k
k
k
k
xx
xx
=
2 2
2 2
2.2010. 2010
2.2010. 2010
k k
k k
x x
x x
2
2
2
2010
2010
2010
2010
kk
k
k
x
x
x
x
=
2
2
2010
2010
k
m
m
=
1
2
2010
2010
k
m
m
0.5
1.0
0.5
Vậ y ta có,
2010
2010
n
n
x
x
=
1
2
2010
2010
n
m
m
mà
lim
n
2
0
2010
2010
n
m
m
( do m>0)
Nên
lim
n
2010 0
2010
n
n
x
x
Đặ t
2010 1
2010
2010 1
n
n
n n
n n
y
x
y x
x y

mà
lim 0
n
ny

=>
lim 2010
n
nx

0.5
0.5
0.5
0.5
3
Theo bấ t đẳ ng thứ c AM-GM, vớ i
0x
, ta có
22
3 2 (1 ) 1
1 1 1 1
2 2
x x x x
x x x x
Áp dụ ng kế t quả trên vớ i a > 0, ta đư ợ c
3 2
3 2 2 2 2 2 2
33
2
1 1 1
11
1
12
a a
b c abc
b c
a a b b c
a
a
a
Bấ t đẳ ng thứ c hiể n nhiên đúng khi a = 0. Tư ơ ng tự , ta có
3 2
32 2 2
3
3 2
32 2 2
3
b b
abc
b c a
c c
abc
c a b
Cộ ng vế theo vế các bấ t đẳ ng thứ c trên ta đư ợ c kế t quả cầ n chứ ng minh.
Đẳ ng thứ c xả y ra khi
abc
1.0
0.5
0.5
0.5
0.5
Vai trò củ a a, b, c là như nhau nên ta giả sử
abc
Kế t hợ p vớ i giả thiế t
0a c
0.5
Do f là hàm số lẻ nên
( 0) (0) (0) 0f f f
và f đồ ng biế n trên R
( ) 0 ( ) ( ) ( ) 0f a f c f a f c
(1)
0.5
Nế u
0b
thì
( ) 0f b
và
0 ( ) ( ) ( )a c a c f a f c f c
( )( ( ) ( )) 0f b f a f c
(2)
Từ (1) và (2)
( ) ( ) ( ) ( ) ( ) ( ) 0f a f b f b f c f c f a
1.0
4
Nế u
0b
thì
( ) 0f b
và
0 ( ) ( ) ( )a c a c f a f c f c
( )( ( ) ( )) 0f b f a f c
(3)
Từ (1) và (3)
( ) ( ) ( ) ( ) ( ) ( ) 0f a f b f b f c f c f a
1.0
Đư ờ ng tròn (C) có tâm I(0 ;1) và bán kính R = 1
Điể m T thuộ c trụ c hoành thì T(t ;0) và điể m M(m;3) thuộ c đư ờ ng thẳ ng y = 3,
ta có phư ơ ng trình đư ờ ng thẳ ng MT :
3 ( ) 3 0
3
x m y m x t m y t
t m
0.5
Do MT là tiế p tuyế n củ a (C) nên
( , ) 1d I MT
, hay
2 2
2 2
31 ( 2 ) 9 ( )
3 ( )
t m t m t t m
t m
0.5