PHÒNG GIÁO D C VÀ ĐÀO T OỤ Ạ Đ THI CH N H C SINH GI I C PỀ Ọ Ọ Ỏ Ấ
HUY NỆ
CHÂU THÀNH L P 9 TRUNG H C S SỚ Ọ Ơ Ở
MÔN TOÁN - NĂM H C 2009 -2010Ọ
Đ chính th c ề ứ Th i gian : 150 phút ( không k phát đ )ờ ể ề
Bài 1. ( 4 đi m)ể
1) Không dùng máy tính, ch ng minh ứ
6 4 2 3 2 2+ − −
là m t s nguyên.ộ ố
2) Rút g n bi u th c: ọ ể ứ
( ) : ( )
x x y y xy x y
x y
−+ +
−
v i x ớ
≥
0; y
≥
0; x
≠
y.
3) Gi i ph ng trình: ả ươ
2 1 4 2 3 2 2 2 2 3 3x x x x+ + − − − − − =
.
Bài 2. ( 3 đi m)ể Tìm s t nhiên n sao cho n + 15 và n – 74 đ u là:ố ự ề
a) s nguyên t .ố ố
b) s chính ph ng.ố ươ
Bài 3. ( 5 đi m)ể Cho đ ng th ng (d): y = 2x + 3 ườ ẳ
a) Tìm trên đ ng th ng (d) nh ng đi m có to đ tho mãn đ ng th c xườ ẳ ữ ể ạ ộ ả ẳ ứ 2 + y2 – 2xy – 4 =
0.
b) T đi m A(–1; 1) v đ ng th ng (d’) vuông góc v i (d) và t đi m B(–3:–3) v đ ngừ ể ẽ ườ ẳ ớ ừ ể ẽ ườ
th ng (d’’) đi qua đi m C(1; 0). Vi t ph ng trình c a các đ ng th ng (d’) và (d’’).ẳ ể ế ươ ủ ườ ẳ
c) Tính di n tích c a tam giác t o b i các đ ng th ng (d), (d’), (d’’) và góc nh n t o b iệ ủ ạ ở ườ ẳ ọ ạ ở
hai đ ng th ng (d) và (d’’) (chính xác đ n phút).ườ ẳ ế
Bài 4. ( 3 đi m)ể Hãy tìm đi m M trên c nh AB c a tam giác ABC sao cho t đi m M đó ta vể ạ ủ ừ ể ẽ
đ c m t đ ng th ng chia tam giác ABC thành hai hình có di n tích b ng nhau. Có m y vượ ộ ườ ẳ ệ ằ ấ ị
trí c a đi m M nh th ?ủ ể ư ế
Bài 5. ( 5 đi m)ể Cho hình thang vuông ABCD (AB//CD,
µ
A
= 900) đ ng cao BH. Đi m M thu cườ ể ộ
đo n HC. T D k đ ng th ng vuông góc v i BM, đ ng th ng này c t BH và BM theoạ ừ ẻ ườ ẳ ớ ườ ẳ ắ
th t E và F.ứ ự ở
a) Ch ng minh b n đi m B, F, H, D cùng n m trên m t đ ng tròn và ứ ố ể ằ ộ ườ EB.EH = ED.EF.
b) Cho AB= 10 cm, BM= 13 cm, DM= 15 cm.Tính đ dài c a các đo n th ng AD, DF và BFộ ủ ạ ẳ
(chính xác đ n 2 ch s th p phân).ế ữ ố ậ
c) Khi M di chuy n trên đo n HC thì F di chuy n trên đ ng nào?ể ạ ể ườ
- H t -ế
PHÒNG GIÁO D C VÀ ỤĐÀO T OẠ H NG D N CH M ƯỚ Ẫ Ấ
CHÂU THÀNH KÌ THI CH N H C SINH GI I C P HUY NỌ Ọ Ỏ Ấ Ệ
L P 9 TRUNG H C S SỚ Ọ Ơ Ở
MÔN TOÁN - NĂM H C 2009 -2010Ọ
Bài 1. ( 4 đi m)ể
1) ( 1 đi m) ể
=
2 2
(2 2) ( 2 1)+ − −
=
2 2 2 1+ − +
= 3.
V y ậ
6 4 2 3 2 2+ − −
= 3, là m t s nguyên.ộ ố
2) ( 1,5 đi m) ể
( ) : ( )
x x y y xy x y
x y
−+ +
−
=
3 3
( ) : ( )
x y xy x y
x y
−+ +
−
=
( )( )
( ) : ( )
x y x xy y xy x y
x y
− + + + +
−
=
( ) : ( )x xy y xy x y+ + + +
=
2
( ) : ( )x y x y+ +
=
x y+
.
3) ( 1,5 đi m) ểĐi u ki n:ề ệ
3
2
x≥
.
Ta có:
2 1 4 2 3 2 2 2 2 3 3x x x x+ + − − − − − =
⇔
2 2
( 2 3 2) ( 2 3 1) 3x x− + + − − =
⇔
2 3 2 2 3 1 3x x− + + − − =
⇔
1 2 3 2 3 1x x− − = − −
Do đó
1 2 3 0x− − ≥
⇔
2x≤
.
K t h p v i đi u ki n ban đ u ta có: ế ợ ớ ề ệ ầ
32
2x≤ ≤
.
Vậy tập hợp nghiệm của ph ng trình là m i x: ươ ọ
32
2x≤ ≤
.
Bài 2. ( 3 đi m)ể
a) ( 1,5 đi m)ể
* N u n – 74 = 2 là s nguyên t (s nguyên t ch n duy nh t) ta tìm đ c n = 76, khi đóế ố ố ố ố ẵ ấ ượ
n+15 = 91 không ph i là s nguyên t . Tr ng h p này không tìm đ c n.ả ố ố ườ ợ ượ
* N u n – 74 là s nguyên t l n h n 2 thì n – 74 là s l suy ra n ph i là s l , khi đó n +ế ố ố ớ ơ ố ẻ ả ố ẻ
15 là s ch n không ph i là s nguyên t . Tr ng h p này cũng không tìm đ c n.ố ẵ ả ố ố ườ ợ ượ
V y không có s t nhi n n đ n + 15 và n – 74 đ u là s nguyên t .ậ ố ự ệ ể ề ố ố
b) ( 1,5 đi m)ể
Gi s n + 15 = aả ử 2 và n – 74 = b2 (a, b
∈
¥
, a<b)
⇒
a2 – b2 = 89
⇒
(a – b)(a + b) =1.89.
T đó tìm đ c ừ ượ a = 45, b = 44.
⇒
n = 2010.
V y v i n = 2010 thì n + 15 và n – 74 đ u là s chính ph ng.ậ ớ ề ố ươ
Bài 3. ( 5 đi m)ể
a) ( 1 đi m) ểThay y = 2x + 3 vào đ ng th c, đ c: xẳ ứ ượ 2+ (2x+3)2– 2x(2x+3) – 4= 0
⇔
x2+ 6x+ 5 = 0
⇔
(x+ 1)(x+ 5) = 0
⇔
x= –1 (
⇒
y= 1), x= –5 (
⇒
y= –7).
Nh ng đi m có to đ tho mãn đ ng th c xữ ể ạ ộ ả ẳ ứ 2 + y2 – 2xy – 4 = 0 là (–1; 1) và ( –5; –7).
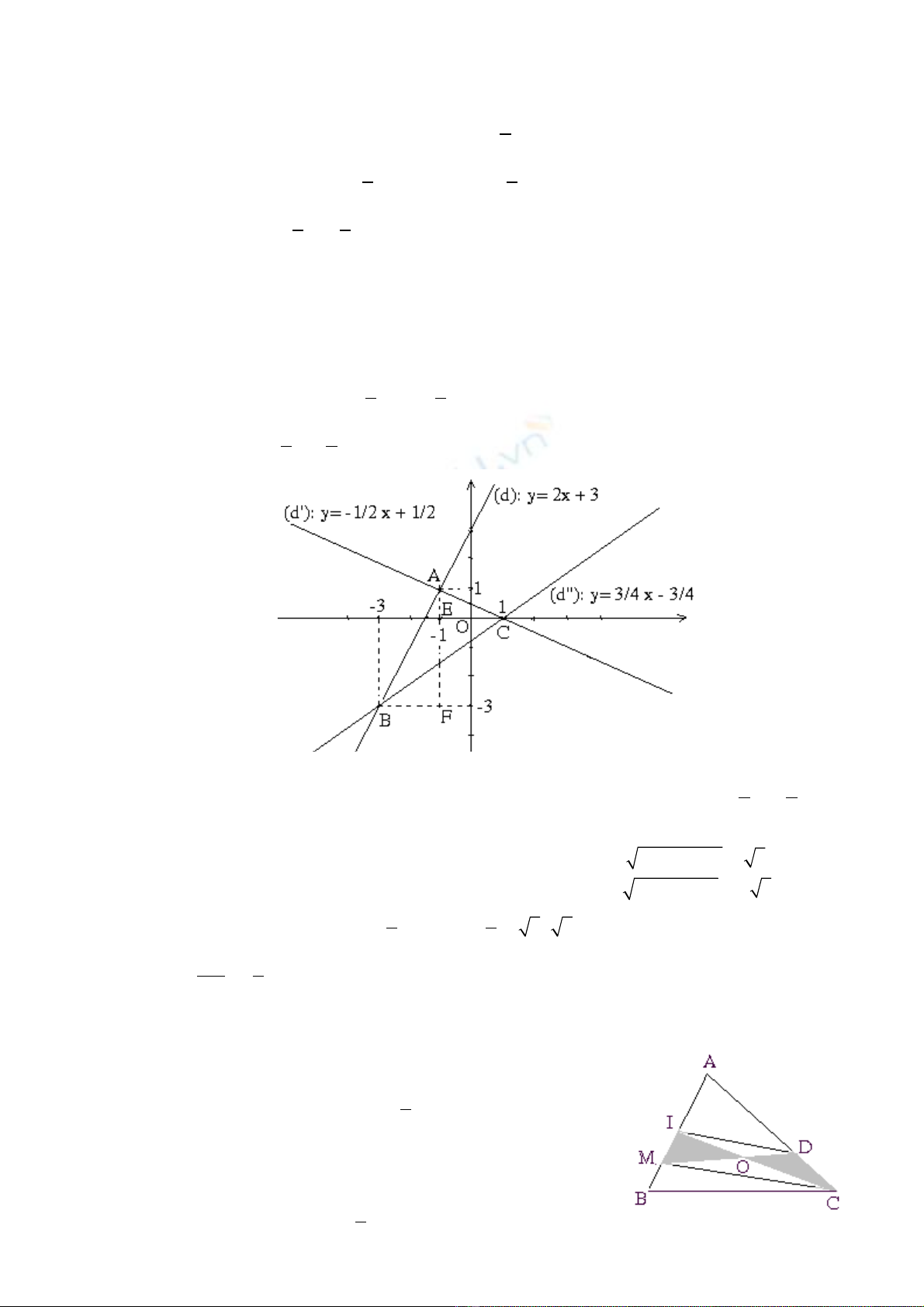
b) ( 2 đi m, k c hình v ) ể ể ả ẽ
* (d’) vuông góc v i (d) nên có d ng: y = ớ ạ
1
2
−
x + b.
(d’) qua A(–1; 1)
⇒
1=
1
2
−
.(– 1) + b
⇒
b=
1
2
Vậy (d’): y =
1
2
−
x +
1
2
.
* (d’’) có d ng y = ax+ bạ
(d’’) đi qua đi m B(–3:–3) ể
⇒
–3= a(–3)+b
⇒
–3a+ b= –3
(d’’) đi qua C(1; 0)
⇒
0= a.1+b
⇒
a+ b= 0.
Ta có h ph ng trình: ệ ươ
3 3
0
a b
a b
− + = −
+ =
.
Gi i h , ta tìm đ c: a = ả ệ ượ
3
4
, b =
3
4
−
.
Vậy (d’’): y =
3
4
x
3
4
−
.
c) ( 2 đi m)ể
(d’) đi qua C(1; 0) vì khi thay to đ C vào (d’) ta đ c đ ng th c đúng 0= ạ ộ ượ ẳ ứ
1
2
−
.1+
1
2
.
Tam giác ABC là tam giác đ c t o b i các đ ng th ng (d), (d’) và (d’’).ượ ạ ở ườ ẳ
Ta có: AE = 1; EC = 2. T tam giác vuông AEC ta đ c AC = ừ ượ
2 2
AE EC+
=
5
.
AF = 4; BF = 2. T tam giác vuông ABF ta đ c AB = ừ ượ
2 2
AF FB+
=
2 5
.
Di n tích tam giác ABC là S = ệ
1
2
.AB.AC =
1
2
.
2 5
.
5
= 5 (đvdt).
tgB =
AC
AB
=
1
2
⇒
·
ABC
= 26034’.
Bài 4. ( 3 đi m)ể
* (1 đi m) ểG i I là trung đi m c a c nh AB. Khi đó đ ngọ ể ủ ạ ườ
th ng IC s chia tam giác ABC thành hai hình tam giác cóẳ ẽ
di n tích b ng nhau Sệ ằ AIC = SAIC =
1
2
SABC.
* (2 đi m, k c hình v ) ể ể ả ẽ Ch n M là trung đi m c a BI.ọ ể ủ
T I v ID// MC (Dừ ẽ
∈
AC).
G i O là giao ọđi m c a MD và IC.ể ủ
Ta có SBCM = SMCI = SMCD =
1
4
SABC. M t khác SặMIO = SCDO.
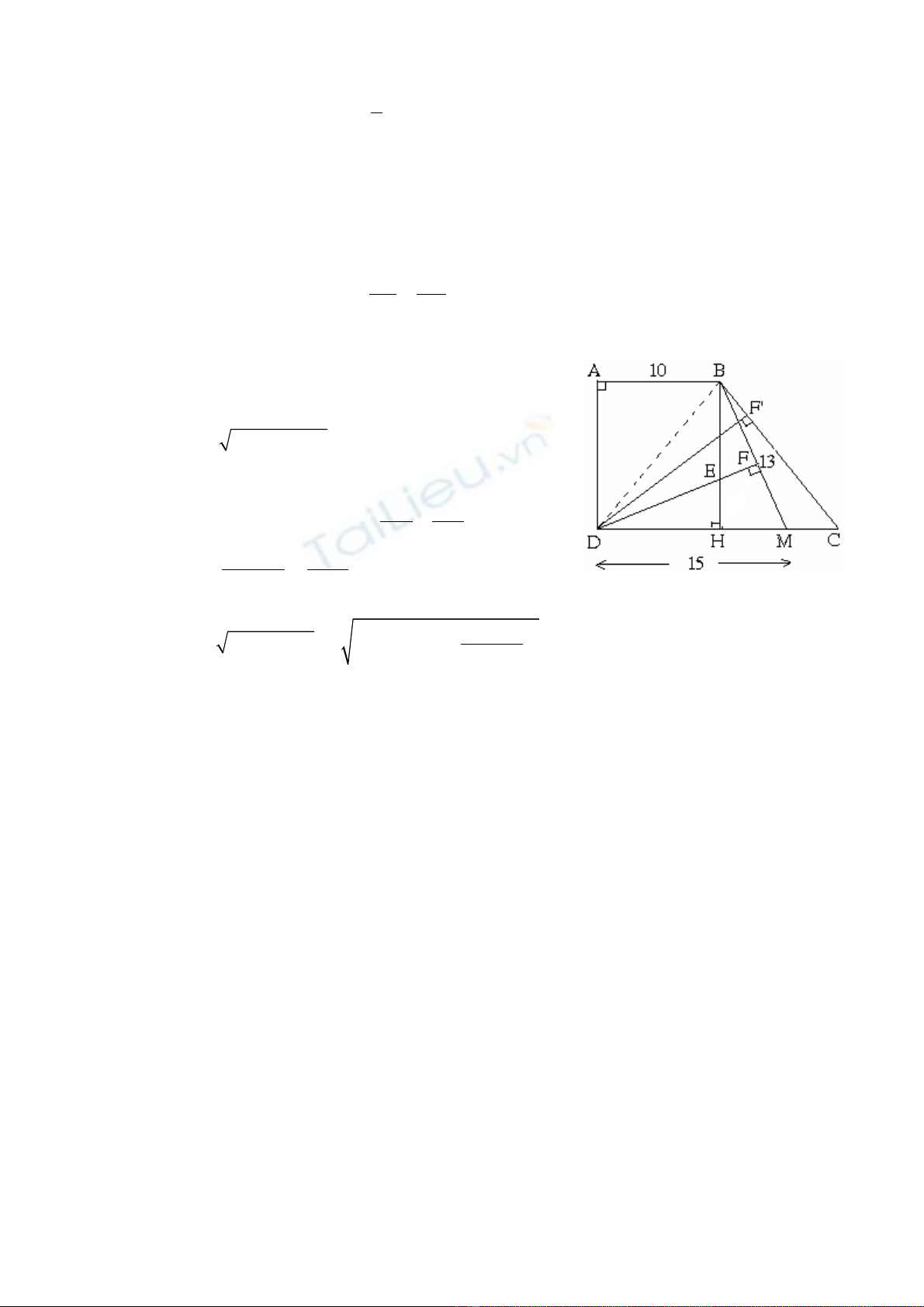
Do đó SBMDC = SBCI = SMAD =
1
2
SABC
V y có hai v trí c a đi m M.ậ ị ủ ể
Bài 5. ( 5 đi m)ể
a) (1,5 đi m)ể
* Ta có
·
·
BFD BHD=
= 900 (gt)
Nên b n đi m B, F, H, D cùng n m trên m t đ ng tròn đ ng kính BD.ố ể ằ ộ ườ ườ
*
FBE∆
~
HDE∆
(g.g) nên
EB ED
EF EH
=
suy ra EB.EH = ED.EF.
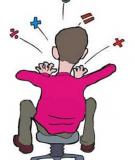
b) (2 đi m)ể
* ABHD là hình ch nh t (vì có 3 góc vuông)ữ ậ
⇒
DH= AB= 10 cm, HM= DM- DH= 5 cm.
Trong tam giác vuông BMH có BM2= BH2+ HM2.
⇒
BH=
2 2
BM HM−
= 12 cm.
Mà AD= BH ( do ABDH là hình ch nh t).ữ ậ
V y AD= 12 cm.ậ
*
MBH∆
~
MDF∆
(g.g) nên
BM MD
BH DF
=
⇒
DF=
.BH MD
BM
=
12.15
13
≈
13,85 (cm)
Trong tam giác vuông BDF có BD2= BF2+ DF2.
⇒
BF=
2 2
BD DF−
=
2 2 2
.
( )
BH MD
AB AD BM
+ −
≈
7,23 cm.
c) (1,5 đi m k c hình v )ể ể ả ẽ
* Ta có
·
BFD
= 900 (gt) và BD c đ nh nên F di chuy n trên đ ng tròn đ ng kính BD.ố ị ể ườ ườ
Gi i h n: - Khi M ớ ạ
→
C thì F
→
F’ (F’
∈
BC v i DF’ớ
⊥
BC).
- Khi M
→
H thì F
→
H.
V y F di chuy n trên cung nh F’H c a đ ng tròn đ ng kính BD. ậ ể ỏ ủ ườ ườ
- H t -ế