$&i
I l.]i:r t:
r: i.,rjr,? - .r: :
.:l:-,:.,, .:.,' i :.
;:,,." L,au
,1 I
x'
I
rl
/t . ,^
ll;c.(.,)
pn rm KSCL DAr HQC NAM 20:-2LAN ]'HrJ'I
MOn: TOAN; tcnOi g
]..1!.'::
I. PHAN CHUNG
: 1. Khio s6t sU bi6n thi6n vd v6 dO thi (C) cua hdm s6 (t).
",,,'2" Cho di6m Mthu6c dO thi (C) co xM =m.Tlm c6c giltrf thUc ciratham s6 *
de tiep tuy6n tai M cit d6 thi (C) tai hai di€m phAn bi6r A. B sao cho MA:3MB
(B nirn gifr'a A vn M). - = J Jt-
{'iu II (2,0 ttihnt) \ L=
i . Gi6i phuong trinh: 4sin2 x.cos x -Zsinzx -sin" = .or"..\
;:. Ciei bAt phuong tr:inh: *'.2" + x.z"nt +IZ <3.2" + 4x2 +gx .
Cfru III 1l,b mAnr) lllr' gi6i han , = SYa
Cf,u IV (1,0 cli,dnt)
Cho hinh ch6p S.ABCD c6 d6y ABCD ld hinh vuOng cpnh bing a. C4nh bOn SA vqdlg g6c
' !' r - "y vA SiA: "Ji . Goi B', D' lAn luqt ld hinh chi€u w6ng goc cua ctiiim l.
vOJ lnat pltang da
tr0n canh SB vA SD. Chirng minh rdng cqnh SC vu6ng g6c v6'i m5t phing (AB'D'). Gsi C'
ra giao di6m .uu ,oat Jr'-L;;;t;;il;. ffi,?;"r;;'ffitilj:16*;,;;:: :,:S
r*f5rsvurvurvL{cL.r.rraL}rudrrti\rrD JJ / vulgalulDL. lrnntllellcncllaKnoicnop).u'L.'D'. *17
Cffu Y (100 tli6nt) Cho bas0thucldr6ngAm x)y,zth6aman x+y*z:Z0Iz, Timgiritri u#-
,rirAt criabi6uthrc: p -{F(",*l| .iFb} +,).iF1; .4> ,[b+V
I[. ]tI{41\ RIENG (3,0 diam)
'.1'h{ sinh clri dngtc chgn nrpt trong hai. phfrn A ho{c B:
A. 'Ihco chu'o'ng frinll chuin
(lf,rr YIa. (2.0 di\rn) Trong mdt phing Oxy cho di6m Me;a)vd'ducrng tr.on (C) c'o
phirong tniih: x' + y' =2x * 6y + 6 = 0.
i.l. Vi6t phuorrg tr"inh duong thdng d di qua ditim M cit ducrng tron (C) rai hai di6rrr p. e
1r sao cho M la trung di6m cua PQ. )(1Y -0= D
2. vi6t phuong trinh duong trdn (c') d6i x#g uii ao*g troq(c ) quu di6m M.
Cffu VIIa .(1,0 di\nl Chrmg minh ring: \^-J) + (t- {) = +
(zn+1)3" =2'".C),,..1+2.22,-,.Cln*,+3.22,-2.C:,,*r *.., +(2n+t)cliil(r-*),
*f +["T ; lu lc^a
L1'.fi)U{l;D-)
\'lL
Tld'i gian ldm bdi; 180 philt, kh6ng k€ thdt gian phdt di
D0 g6m: 02 trang
crro rAr cA cAc rni srNH (7,0 diam)
r (2,0 ili\m)Cho hdm s6 y - -t +3*' -! (t).
'22\-'l-
Trung Il2
www.VNMATH.com
oii.,rrung rn4t phang Oxy, cho tam gi6c'ABC'c6 A(l;3). Ducrng phdn gi6c trong cria goc B
:nim tr6n duong thing d, c6 phuong trinh ld: x - y -l = 0 va'dulng "uo *n6t ph6t tt dinh C
lina* tr6n ducmg th8ng drc6 phucrng trinh lA:x + 3y + 2- 0 . Vi6trphuong trinh duhng thang
.. ::.i.-i," i: r.
l"r.:.'j:', 2 2
: 0"'" 2.Cho elfp (E): l* * =t, gqi F,(-.;0)
..'-'.,. r \ / 25 16
,.r ,cho dO ddi FrM co gi6 tri 16n nnat.
. Cf,u VIIb. (1,0 itidm) Cho mQt da gi6c
l6y trr 3 trong 32 di6m Ar, Az, ..., A:z
tlat
canh cita da gi6c l6i ArA2. ..An.
': I
'..::,:,.-i, r I i
i{,. .F +cfwri rr., ',. - '- .Jl.l
:'; l l. .,
. ilr 'l
bao nhi6u tam gi6c c6 ba dinh
lutn gi6c khdng c6 cqnh nho lir
.chria cpnh BC cira tetm gi6c ABC. *- ly-q>O : ,:
ld,mQt ti€u di6m cira (E). Tim di6m M tr6n (E) sao
[t '4
l6i ArA2...A:2. Hoi c6
sao cho mdi canh cira
frrq
L.rE'T]
lrri I -----
(Cdn bd coi thi khdng gidi thich gi th€m)
Trang2/2
I.j .-
! -rl I
www.VNMATH.com
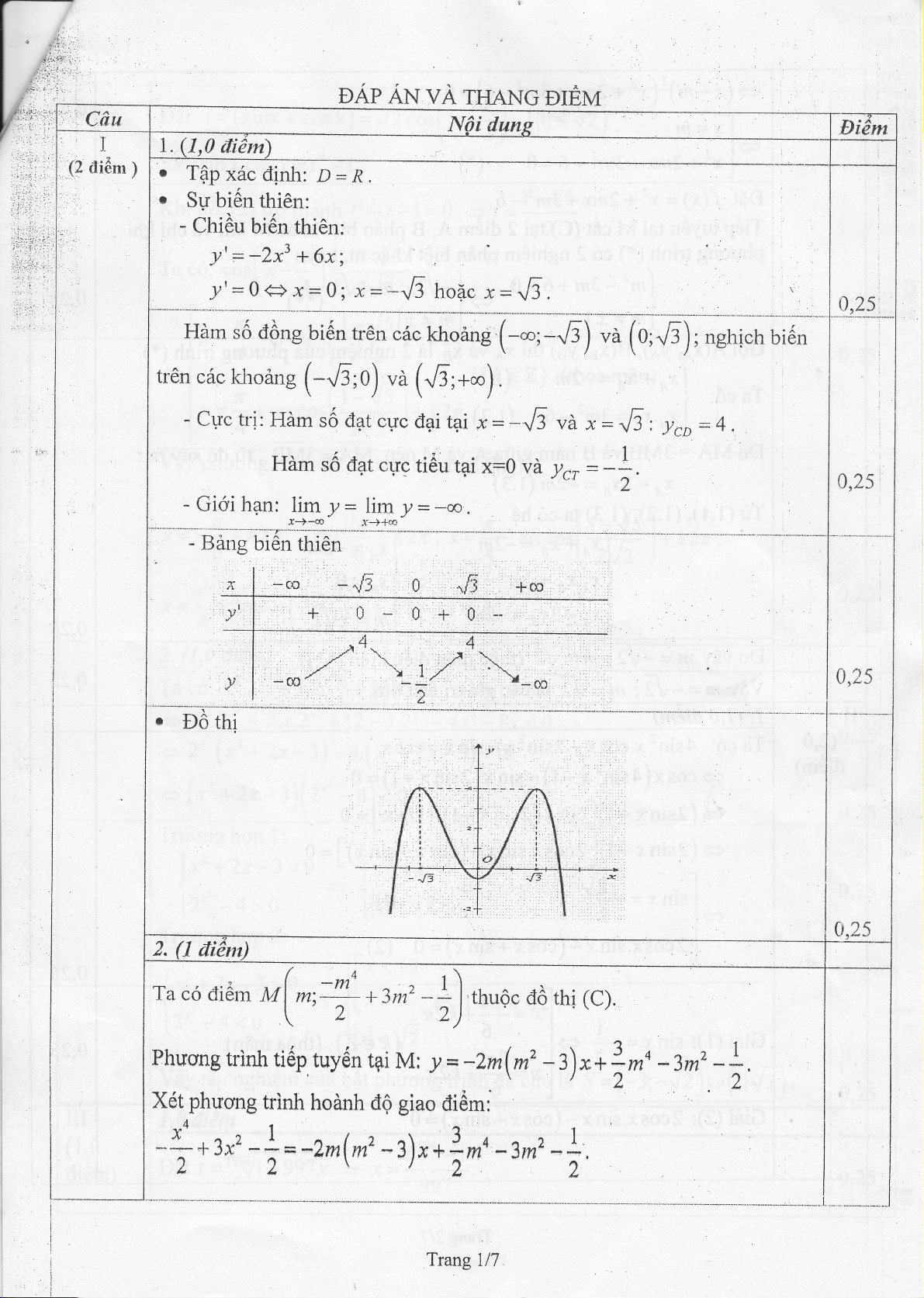
I. (1,0 tli1m
2. (1 iti
PAp AN VA THANG EIEM
,T I
'(2 ili0m )T0px6cdinh: D=R,
Su bi6n thi6n:
- Chi6u bi6n thi6n:
!'= -2x3 + 6x;
!'=0g;s=0; x=--rE hoAc x=$.
Hdm '6 AOng bi6n trdn c6c kho6n* (-*'-..6) va (o;"-6); nehich bicn
tron c6c khoang (-16'o) va (..6;**).
- CUc tri: Hdrm sO dat cuc dpi t4r x= -..,6 vdL x: 1f, 1 lcn = 4 .
Hdm sO dat cgc ti6u tpi x:0 vd lcr
- Gi6i han: lim y: lim ! =-oo.
-t-+-co x-)+o
- BAng bi€n thi6n
r DO thi
Ta c6 diOrn
0,25',
4,25
4,25
0,25
I
2'
+ : 0 - 0 ,+ '0.',,_
Phuong trinh ti6p tuyiln ei M: ! = -Zm(^' -3)x+ |*- *U*, *I .
AL
Xdt phuong trinh hodnh d9 giao dii5m:
-^4 1
-** 3xz -l=-z*(,n' -3)x+ 1*^ -3,r' -!.
2 2 2' z',
Trang Il7
www.VNMATH.com
<+ (, - *)' (r'
f*=*
.'-tt I
-- L"t +Zmx +
-6)=o
(-)'
EAt /(x) = x2 1- 2mx +3m2 - 6 -
Ti0p tuy6n t4i M clt 1C; t4i 2 di6rn A, B phdn bi6t kh6c M khi vd clii khi
phucrng trinh (*) c6 2 nghiQm ph6n bipt kh6c m, hay :
Iaco:' l*n'*u :3m2 - 6 (t.z)
Do IWt : 3MB vd B nim gitaA vd M n6n M{ = 3MB , tri d6 suy ra :
1- -?- -_1 -^fr r\
""A - )xB = -2m 0.:)
rr (1.1), (r .rr,rr,r)^?::r)r*r* [". : _2m
),i,,*"=r*'-u *l;: =Q
I" " l'6
1", - 3x, : -2nt l* - tJt
Do vAy * = -Ji; m:J7 (tnOu mdn didu kiQn (**)).
YQy m = -Ji ; m = rlz n cilc gi|tri cAn tim.
Ta c6: 4sin2 x.cos x - Zsin2x - sinx = cosx
{+ cos"(4rin" - 1)- sinx(zsinx + 1)= g
<* (zsinx + l)[cosx(2sin" - 1)- sin*] = o
e (2sinx + t)[zcosx.sinx * (cosx + sinx)] - o
l1
lsinx--- (l)
c+l 2
[z ,o, x. sin x - (cos x +:sin .r) - 0 (2)
Giai (1): (tr e z) . (th6a mdn).
,
Gi6i (2): 2cosx.sinx - (cosx + sinx)= 0
-r 2rnx +3rnz
3m2 -6=0
(2,0
*.4 \
Cllem)
1.4,.'t1t
iiiii,f :,1
T
I *--L+kur
sinx=-t ol 6
2 I *=A+k2n
L6
Trang2lT
4,25
www.VNMATH.com
!i': ,, :
+2sinr.cos *=t'-'1.
Khi d6, (2) tro thinh t2 - t- I = 0 e t -LS
2
Taco: .or["-z'']-1-S
---("" 4 ) 2J,
I *=o -u,""or[t-f.) +k2n
| 4 \zJz)
el ) ,_'., ,(k=z).6naamdn)
l*-o*ur".orf!-fl +kzn
| 4 \2J2)
Vpy phuong trinh dE cho c6 c6c nghigm ln
*= -1+ k2n, * =!+ k2tr, x=L- ur""orf!:gl + katr,
6 6 4 -[zJz ) --'
n (t r-\
.rr=1+arccosl -^ p l+kzn (kez)
4 lzJz) \
J,25
*,25
2. (1,0 clidm)
Ta c6: *'.2" + x.2"*1 +r2 <3.2*' + 4x2 +Bx
o *'.2"' +2.x.2" +12-3.2*' -4x2 -Bx<o
e 2*' (x' + 2x 3) a.(*t + 2x 3) . 0
o (r' +2x -t)(r' - o) . o
l*'"*2'x'-3<o [-3<x<1
1 ci I - <+'-3<rc<-Ji.
lzu -4>o [l'l'.D
Truong hgp 2:
, ^ llx<-3
[*'*Zx-3>o ll'"- -
1"",-'" <+{1"t1 <+I<*<Ji.
l2* _4<o [u.o
Vfly tap nghiQm'cfra bdt phuong trinh dd cho ld S = (-:;-.,n) , (r;rD ) ,i],25
l
+,25 ]
I
l
,).2s 1
'*--l
l
r.),25 ]
ili
(l,r)
di6m)
1,0 &i6m
Ddt r= lleea _ 1
997
+997 xn1t
'J yLJ
Trung3/7
www.VNMATH.com