Trang 1/6 - Mã đề thi 013
SỞ GIÁO DỤC & ĐÀO TẠO VĨNH PHÚC
TRƯỜNG THPT NGUYỄN VIẾT XUÂN
Mã đề thi: 013
ĐỀ THI KSCL LẦN 3 NĂM HỌC 2020-2021
Môn thi: TOÁN 12
Thời gian làm bài: 60 phút;
(50 câu trắc nghiệm)
Câu 1: Cho cấp số cộng
( )
n
u
với
13u= −
và
2
3u=
. Công sai
d
của cấp số cộng đó bằng
A.
6−
. B.
0
. C.
. D.
9−
.
Câu 2: Trong không gian
Oxyz
, hình chiếu vuông góc của điểm
( )
2; 3; 4A
trên trục
Oz
có tọa độ là
A.
( )
2; 0; 4
. B.
( )
0; 3; 4
. C.
( )
2; 3; 0
. D.
( )
0; 0; 4
.
Câu 3: Cho hình trụ có bán kính đáy
2ra
và độ dài đường sinh
la
. Diện tích xung quanh của hình
trụ đã cho bằng
A.
2
8a
π
. B.
2
2a
π
. C.
2
a
π
. D.
2
4a
π
.
Câu 4: Giá trị lớn nhất của hàm số
1
yxx
= −
trên đoạn
[ ]
1; 2
là:
A.
[ ]
1;2
3
2
max y =
. B.
[ ]
1;2
0max y =
. C.
[ ]
1;2
2max y =
. D.
[ ]
1;2
5
2
max y =
.
Câu 5: Số giao điểm của đồ thị hàm số
2
( 1)( )yx xx=−+
với trục
Ox
là:
A.
1
. B.
3
. C.
. D.
2
.
Câu 6: Trong không gian
Oxyz
, cho hai điểm
( )
20; 8; 2A−
và
( )
20; 4; 4B−
. Trung điểm của đoạn thẳng
AB
có tọa độ là
A.
( )
20; 2;1
. B.
( )
20; 2;1−
. C.
( )
20; 2; 2
. D.
( )
0; 6;3−
.
Câu 7: Đường tiệm cận ngang của đồ thị hàm số
28
2
x
yx
−
=−+
có phương trình là
A.
2y= −
. B.
4y= −
. C.
2x= −
. D.
2x=
.
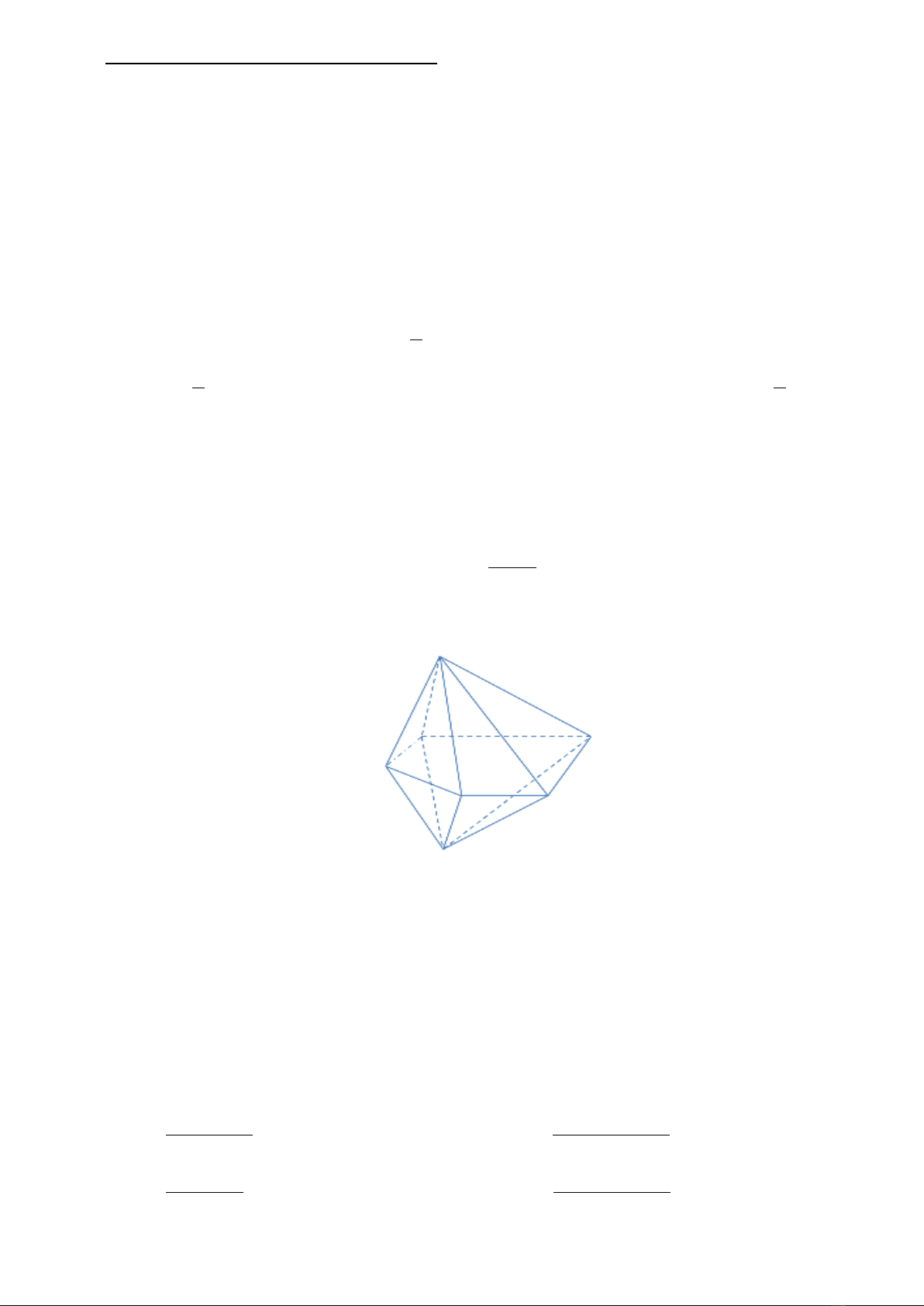
Câu 8: Hình đa diện ở hình vẽ bên dưới có tất cả bao nhiêu cạnh?
A.
11
. B.
14
. C.
10
. D.
15
.
Câu 9: Trong các khẳng định sau, khẳng định nào sai ?
A.
0dxC=
∫
. B.
dx xC= +
∫
.
C.
cos d sinxx x C= +
∫
. D.
sin d cosxx x C= +
∫
.
Câu 10: Với
a
,
là hai số thực dương tùy ý,
( )
2
ln ab
bằng
A.
2ln lnab+
. B.
ln 2lnab+
. C.
2.ln .lnab
. D.
ln 2lnab−
.
Câu 11: Có bao nhiêu cách xếp 5 học sinh thành một hàng dọc?
A.
120
. B.
1
. C.
5
. D.
25
.
Câu 12: Đạo hàm của hàm số
2
2
log 2y xx 
là
A.
2
2 1 ln 2
'2
x
yxx

. B.
2
21
'2 ln 2
x
yxx

.
C.
2
21
'2
x
yxx

. D.
2
21
'2 ln 2
x
yxx

.
Trang 2/6 - Mã đề thi 013
Câu 13: Cho hàm số
( )
y fx=
có bảng biến thiên như hình vẽ dưới đây.
Giá trị cực tiểu của hàm số đã cho là
A.
0x=
. B.
0y=
. C.
1y=
. D.
1y= −
.
Câu 14: Họ tất cả các nguyên hàm của hàm số
( )
1f x cosx= +
là
A.
x cosx C++
. B.
sinx xC++
. C.
xcosxC−+
. D.
sinx xC−+
.
Câu 15: Họ tất cả các nguyên hàm của hàm số
( )
x
fx e=
là
A.
x
e
. B.
x
eC−+
. C.
x
e−
. D.
x
eC+
.
Câu 16: Tập xác định của hàm số
( )
4
2
yxx
−
= −
là
A.
{ }
\ 0;1D=
. B.
( ) ( )
; 0 1;D= −∞ ∪ +∞
.
C.
D=
. D.
( )
0;1D=
.
Câu 17: Cho khối cầu
T
có tâm
O
bán kính
R
. Gọi
S
và
V
lần lượt là diện tích mặt cầu và thể tích
khối cầu. Mệnh đề nào sau đây là đúng ?
A.
3
4
3
VR
. B.
2
4
3
SR
π
. C.
3
4VR
π
. D.
2
4SR
π
.
Câu 18: Tập nghiệm
S
của bất phương trình
( )
2
log 2 2x−>
là
A.
( )
;6S= −∞
. B.
( )
2; 6S=
. C.
( )
4;S= +∞
. D.
( )
6;S= +∞
.
Câu 19: Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
`
x
-1
O
y
1
-1
A.
42
21yx x=−−
. B.
331yx x=−+ −
.
C.
42
21yx x=−+ −
. D.
331yx x=+−
.
Câu 20: Cho hàm số
( )
y fx=
có đồ thị như hình vẽ.
Hàm số đã cho đồng biến trên khoảng nào?
A.
( )
;1−∞ −
. B.
( )
1;3−
. C.
( )
0;+∞
. D.
( )
1;1−
.
Câu 21: Cho hàm số
( )
y fx=
có bảng biến thiên như sau:
Trang 3/6 - Mã đề thi 013
Số nghiệm thực phân biệt của phương trình
( )
2 90fx+=
là
A.
1
. B.
4
. C.
3
. D.
2
.
Câu 22: Cho hàm số
()y fx=
liên tục trên đoạn
[ 3; 4]−
và có đồ thị như hình vẽ.
Gọi
M
và
m
lần lượt là các giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn
[ 3 ;1]−
. Tích
.Mm
bằng
A.
3−
. B.
0
C.
12
. D.
4
.
Câu 23: Cho hàm số
( )
y fx=
liên tục trên
và có bảng biến thiên như sau:
Số điểm cực trị của hàm số đã cho là
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 24: Cho biết
( )
3
2020x
Fx x= −
là một nguyên hàm của hàm số
( )
fx
. Tìm
( )
2dI fx x x= +


∫
A.
32
2020x
I xxC= −++
B.
32
2020
ln 2020
x
I xxC= −++
.
C.
3
2020 2
x
I x xC= −+ +
. D.
2
2020 ln 2020 2
x
I xC= −+
.
Câu 25: Cho phương trình
( )
2
33
log 3 4log 4 0xx− −=
. Bằng cách đặt
3
logtx=
phương trình đã cho trở
thành phương trình nào dưới đây?
A.
2
4 30tt− −=
. B.
2
4 40tt− −=
.
C.
2
2 30tt− −=
. D.
2
3 20tt− +=
.
Câu 26: Cho khối lăng trụ đứng tam giác
.ABC A B C
′′′
có
3AA a
′=
, đáy
ABC
là tam giác vuông tại
A
và
2,AC a AB a= =
. Thể tích
V
của khối lăng trụ đã cho là
A.
3
6Va=
. B.
3
3
a
V=
. C.
3
Va=
. D.
3
3Va=
.
Câu 27: Cho hình nón có bán kính đáy bằng
a
và diện tích toàn phần bằng
π
2
5a
. Độ dài đường sinh
l
của hình nón bằng
A.
3la=
. B.
5la=
. C.
4la=
. D.
2la=
.
Câu 28: Một hộp đựng
20
viên bi gồm
7
viên bi màu vàng,
5
viên bi màu đỏ và
8
viên bi màu xanh.
Có bao nhiêu cách chọn 6 viên bi trong hộp đó mà không có viên bi nào màu vàng?
A.
66
20 13
CC−
. B.
66
20 7
CC−
. C.
6
13
C
. D.
6
7
C
.
Trang 4/6 - Mã đề thi 013
Câu 29: Cho hình chóp tam giác
.S ABC
có
( )
,3SA ABC SA a⊥=
, đáy
ABC
là tam giác vuông cân tại
A
, biết
32BC a=
. Số đo của góc giữa cạnh
SB
và mặt phẳng
( )
ABC
bằng
A.
0
90
. B.
0
60
. C.
0
30
. D.
0
45
.
Câu 30: Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
để hàm số
32
1y x mx mx=− ++
đồng
biến trên khoảng
( )
;−∞ +∞
. Số phần tử của tập
S
là
A.
21
. B.
4
. C.
10
. D.
6
.
Câu 31: Cho hàm số
( )
=y fx
có bảng biến thiên như hình dưới.
||
-1
∞
1
0
+
∞
∞
∞
+
0
1
y
y'
x
+
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
( )
=y fx
là
A.
4
. B.
3
. C.
. D.
1
.
Câu 32: Biết
( )
Fx
là một nguyên hàm của hàm số
( )
11
,;
2 1 ln
fx x e
xx

= ∀ ∈ +∞

+
thỏa mãn
( )
12F=
. Giá trị của
( )
8
Fe
là
A.
3
. B.
8
. C.
9
. D.
4
.
Câu 33: Cho hình bát diện đều cạnh
4a
. Gọi
S
là tổng diện tích của tất cả các mặt của hình bát diện đều
đó. Khi đó
S
bằng:
A.
2
83Sa=
. B.
2
16 3Sa=
.
C.
2
32 3Sa=
. D.
( )
2
32 3 1Sa= +
.
Câu 34: Cho
35
a
=
. Tính
25
2log 27
theo
a
.
A.
3
2
a
. B.
3
a
. C.
3
2a
. D.
2
3
a
.
Câu 35: Tiếp tuyến của đồ thị hàm số
321yx x=−−
tại điểm
( )
1; 2A−
có phương trình
A.
1yx= −
. B.
3yx= −
. C.
1yx= +
. D.
3yx=−−
.
Câu 36: Cắt hình nón đỉnh
S
bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền
bằng
2a
. Thể tích của khối nón theo
a
là
A.
3
4
3
a
π
. B.
3
3
a
π
. C.
3
a
π
. D.
3
4a
π
.
Câu 37: Một người gửi tiết kiệm vào một ngân hàng với lãi suất
6,9% /r=
năm. Biết rằng nếu không rút
tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tính lãi cho năm tiếp theo.
Hỏi sau ít nhất bao nhiêu năm nữa người đó thu được (cả vốn và lãi) gấp bốn lần số tiền gửi ban đầu, giả
định trong khoảng thời gian này, lãi suất không thay đổi và người đó không rút tiền ra?
A.
21
năm. B.
19
năm. C.
18
năm. D.
22
năm.
Câu 38: Cho hình chóp
.S ABCD
có đáy là hình vuông cạnh
a
. Cạnh bên
7SA a=
và vuông góc với
đáy
( )
ABCD
. Tính theo
a
diện tích mặt cầu ngoại tiếp khối chóp
.S ABCD
.
A.
2
12 a
π
. B.
2
18 a
π
. C.
2
9a
π
. D.
2
36 a
π
.
Câu 39: Cho hàm số
( )
fx
liên tục trên
thỏa mãn
( ) ( )
2
2. ,
1
x
xe
fx f x x
x
−
′
= − ∀∈
+
và
( )
01f=
. Tính
( )
1f
A.
ln 2
e
. B.
ln 2 e
e
+
. C.
1 ln 2+
. D.
ln 2e
e
.
Trang 5/6 - Mã đề thi 013
Câu 40: Chọn ngẫu nhiên một số từ tập các số tự nhiên có năm chữ số đôi một khác nhau. Xác suất để số
được chọn có mặt đồng thời cả ba chữ số
1, 2
và
3
là
A.
23
420
. B.
23
378
. C.
11
140
. D.
11
126
.
Câu 41: Cho hàm số
( )
y fx=
có đạo hàm
( ) ( ) ( )
3
2
52 1fx x x x
′= −+
. Khi đó số điểm cực trị của hàm
số
2
1
x
yf
x

=
+

là
A.
5
. B.
4
. C.
. D.
3
.
Câu 42: Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng
3
lần đường kính của đáy ;
một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng của cốc
nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó ( như hình vẽ ) thì thấy nước trong cốc tràn
ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu ( bỏ qua bề dày của
lớp vỏ thủy tinh).
A.
2
3
. B.
5
9
. C.
4
9
. D.
1
2
.
Câu 43: Cho hàm số
( )
y fx=
liên tục trên
và có đồ thị như hình vẽ dưới đây.
Tập hợp tất cả các giá trị thực của tham số
m
để phương trình
( )
4 2 90
x
fm− +=
có nghiệm là
A.
[
)
4;+∞
. B.
9
1; 2


. C.
( )
;6−∞
. D.
( )
0;+∞
.
Câu 44: Cho hình chóp
.S ABC
có
2, 3, 4= = =SA a SB a SC a
và
60 , 90==°=°ASB BSC ASC
. Tính thể
tích
V
của khối chóp
..S ABC
A.
3
42
3
=a
V
. B.
3
22=Va
. C.
3
2=Va
. D.
3
22
9
=a
V
.
Câu 45: Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông tại
, 3 , 4 .B AB a BC a= =
Cạnh bên
SA
vuông góc với đáy. Góc tạo bởi giữa
SC
và đáy bằng
60°
. Gọi
M
là trung điểm của
AC
, tính khoảng
cách giữa hai đường thẳng
AB
và
SM
.
A.
5 237
79 a
. B.
8 237
79 a
. C.
10 237
79 a
. D.
7 237
79 a
.
Câu 46: Cho hàm số
( )
fx
. Hàm số
( )
y fx
′
=
có đồ thị như hình bên.
O
x
y
1−
1−
1
3
1
2
2−