MÃ ĐỀ: 562
TRƯỜNG CĐ KT CAO THẮNG ĐỀ THI HK1 (2013-2014) LẦN 1
KHOA ĐIỆN TỬ - TIN HỌC MÔN: LÝ THUYẾT TÍN HIỆU
LỚP: CĐ ĐTTT 12A, B
THỜI GIAN LÀM BÀI: 75 PHÚT
NGÀY THI: 03/01/2014
(Sinh viên được sử dụng 1 tờ A4 viết tay)
Bài 1 (2đ):
Hãy cho biết các tín hiệu sau là tín hiệu công suất hay năng lượng? Tại sao? Hãy
tính năng lượng hoặc công suất của tín hiệu tương ứng?
a) 𝑥1(𝑡)=2𝑒−3𝑡.1(𝑡)
b) 𝑥2(𝑡)=3.1(𝑡)
Bài 2 (2đ):
Cho tín hiệu 𝑥(𝑡)=𝑒−2𝑡.1(𝑡). Hãy xác định phổ, mật độ phổ năng lượng, hàm tự
tương quan của 𝑥(𝑡). Tính năng lượng của tín hiệu 𝑥(𝑡).
Bài 3 (3đ):
Tín hiệu 𝑥(𝑡)=𝑆𝑎(2𝑡) được đưa qua mạch lọc như hình, với 𝑘(𝑡)=𝑆𝑎2(2𝑡).
Hãy tìm 𝑦(𝑡) ở đầu ra mạch lọc và tính năng lượng 𝐸𝑦 của nó.
Biết tín hiệu 𝑦(𝑡)=𝑘(𝑡)∗𝑥(𝑡)
)(ty
)(tx
)(tk
Bài 4 (3đ):
Cho tín hiệu điều chế: 𝑦𝐴𝑀(𝑡)=[1+𝑥(𝑡)]cos⁡𝜔0𝑡
Với 𝑥(𝑡)=2cos(Ω1𝑡)+3𝑐𝑜𝑠(Ω2𝑡);
𝜔0=2𝜋105⁡𝑟𝑎𝑑/𝑠;⁡Ω1=𝜋103𝑟𝑎𝑑/𝑠;⁡Ω2=2𝜋103𝑟𝑎𝑑/𝑠
a. Tìm 𝑦𝐴𝑀(𝑡). Xác định 𝑌𝐴𝑀(𝜔). Vẽ phổ 𝑌𝐴𝑀(𝜔).
b. Xác định Ψ𝑦𝐴𝑀(𝜔). Tính 𝑃𝑦𝐴𝑀và băng thông của tín hiệu điều chế.
***Hết***
Ngày 21 tháng 12 năm 2013
Bộ Môn GV ra đề
Lưu Văn Đại
ĐÁP ÁN ĐỀ 562
Câu 1
a.
𝑥1(𝑡) là tín hiệu năng lượng vì khi t →
thì x(t) → 0
0.5
0.5
b.
𝑥2(𝑡) là tín hiệu công suất vì khi t →
thì y(t) → 3≠0
0.5
2
9
3
2
1
lim3
2
1
lim
0
22
dt
T
dt
T
P
T
T
T
T
T
y
0.5
Bài 2
𝑿(𝝎)=𝟏
𝜶+𝒋𝝎=𝟏
𝟒+𝝎𝟐
0.5
𝝓(𝝎)=|𝑿(𝝎)|𝟐=𝟏
𝜶𝟐+𝝎𝟐=𝟏
𝟑𝟐+𝝎𝟐
0.5
𝝋𝒙(𝝉)=𝟏
𝟐𝜶𝒆−𝜶|𝝉|=𝟏
𝟒𝒆−𝟐|𝝉|⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡⁡(𝝋𝒙(𝝉)↔𝝓(𝝎))
0.5
𝑬𝒙=𝝋𝒙(𝟎)=𝟏
𝟒𝒆𝟎=𝟏
𝟒
0.5
Bài 3
𝑿(𝝎)=𝝅
𝟐∏(𝝎
𝟒)
0.5
𝑲(𝝎)=𝝅
𝟐⋀(𝝎
𝟒)
0.5
𝒀(𝝎)=𝝅𝟐
𝟒(𝟏
𝟐∏(𝝎
𝟒)+𝟏
𝟐⋀(𝝎
𝟐))
0.5
𝒚(𝒕)=𝝅
𝟒𝑺𝒂(𝟐𝒕)+𝝅
𝟖𝑺𝒂𝟐(𝒕)
0.5
𝑬𝒚=𝝅
𝟒.𝝅
𝟐+𝝅
𝟖.𝟐
𝟑.𝝅
𝟏=𝟓𝝅𝟐
𝟐𝟒 =𝟐.𝟎𝟓
0.5
Vẽ hình
0.5
Bài 4
a.
𝒚𝑨𝑴(𝒕)=𝒄𝒐𝒔(𝝎𝟎𝒕)+𝟐.𝒄𝒐𝒔(𝛀𝟏𝒕).𝒄𝒐𝒔(𝝎𝟎𝒕)+
𝟑.𝒄𝒐𝒔(𝛀𝟐𝒕).𝒄𝒐𝒔(𝝎𝟎𝒕)=𝒄𝒐𝒔(𝝎𝟎𝒕)+𝒄𝒐𝒔(𝝎𝟎−𝛀𝟏)+
𝒄𝒐𝒔(𝝎𝟎+𝛀𝟏)+𝟑
𝟐𝒄𝒐𝒔(𝝎𝟎−𝛀𝟐)+𝟑
𝟐𝒄𝒐𝒔(𝝎𝟎+𝛀𝟐)
0.5
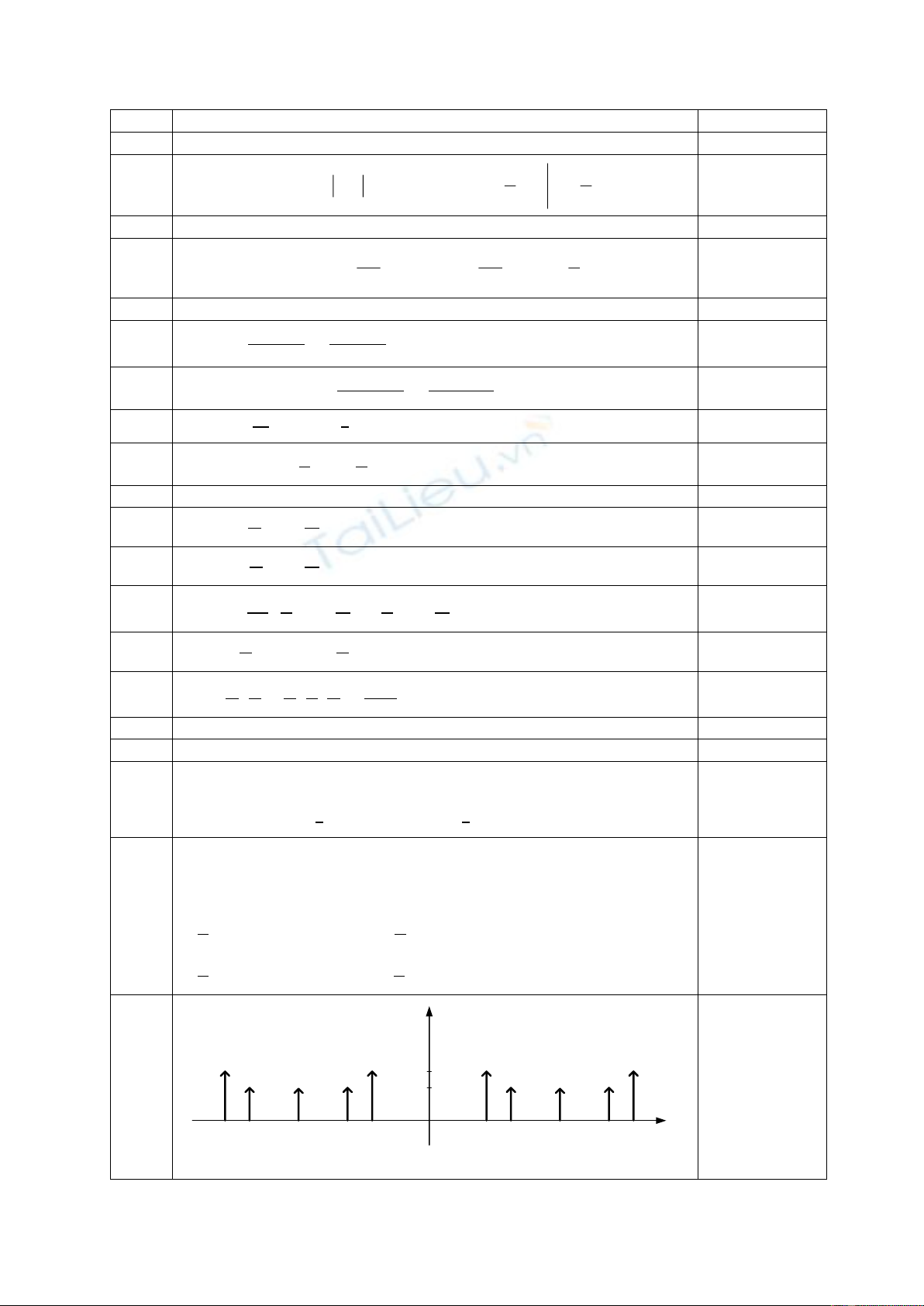
𝒀𝑨𝑴(𝝎)=⁡𝝅𝜹(𝝎−𝝎𝟎)+𝝅𝜹(𝝎+𝛚𝟎)
+⁡𝝅𝜹(𝝎−(𝝎𝟎−𝛀𝟏))+⁡𝝅𝜹(𝝎+(𝝎𝟎−𝛀𝟏))
+⁡⁡𝝅𝜹(𝝎−(𝝎𝟎+𝛀𝟏))+⁡𝝅𝜹(𝝎+(𝝎𝟎+𝛀𝟏))
+𝟑
𝟐𝝅𝜹(𝝎−(𝝎𝟎−𝛀𝟐))+𝟑
𝟐𝝅𝜹(𝝎+(𝝎𝟎−𝛀𝟐))
+𝟑
𝟐𝝅𝜹(𝝎−(𝝎𝟎+𝛀𝟐))+𝟑
𝟐𝝅𝜹(𝝎+(𝝎𝟎+𝛀𝟐))
0.5
1.5π
)(
AM
Y
0
π
A B C
D
E
-A -D -E
-B
-C
0.5
b.
𝚿𝑨𝑴(𝝎)=⁡𝟐𝝅[𝟏
𝟒𝜹(𝝎−𝝎𝟎)+𝟏
𝟒𝜹(𝝎+𝛚𝟎)]
+𝟐𝝅[𝟏
𝟒𝜹(𝝎−(𝝎𝟎−𝛀𝟏))+𝟏
𝟒𝜹(𝝎+(𝝎𝟎−𝛀𝟏))]
+𝟐𝝅[𝟏
𝟒𝜹(𝝎−(𝝎𝟎+𝛀𝟏))+𝟏
𝟒𝜹(𝝎+(𝝎𝟎+𝛀𝟏))]
+𝟐𝝅[𝟗
𝟏𝟔𝜹(𝝎−(𝝎𝟎−𝛀𝟐))+ 𝟗
𝟏𝟔𝜹(𝝎+(𝝎𝟎−𝛀𝟐))]
+𝟐𝝅[𝟗
𝟏𝟔𝜹(𝝎−(𝝎𝟎+𝛀𝟐))+𝟗
𝟏𝟔𝜹(𝝎+(𝝎𝟎+𝛀𝟐))]
0.5
𝑷𝒚𝑨𝑴 =𝟏
𝟒.𝟐+𝟏
𝟒.𝟒+ 𝟗
𝟏𝟔.𝟒=𝟐𝟏
𝟒=𝟑.𝟕𝟓
0.5
𝑩𝑾=𝟐𝝎𝒎𝒂𝒙 =𝟐(𝝎𝟎+𝛀𝟐)=𝟐(𝟐𝝅𝟏𝟎𝟓
𝟐𝝅 +𝟐𝝅𝟏𝟎𝟑
𝟐𝝅 )
=𝟐𝟎𝟐⁡𝑲𝑯𝒛
0.5
Chú ý:
A = 𝝎𝟎 = 200000π
B = 𝝎𝟎+𝛀𝟏=⁡201000π
C = 𝝎𝟎+𝛀𝟐=⁡202000π
D = 𝝎𝟎−𝛀𝟏= 199000π
E = 𝝎𝟎−𝛀𝟐=⁡198000π