OLYMPIC C H C TOÀN QU C L N TH XXIII NĂM 2011Ơ Ọ Ố Ầ Ứ

Đ THI MÔN NGUYÊN LÝ MÁYỀ
CÓ NG D NG CÔNG NGH THÔNG TINỨ Ụ Ệ
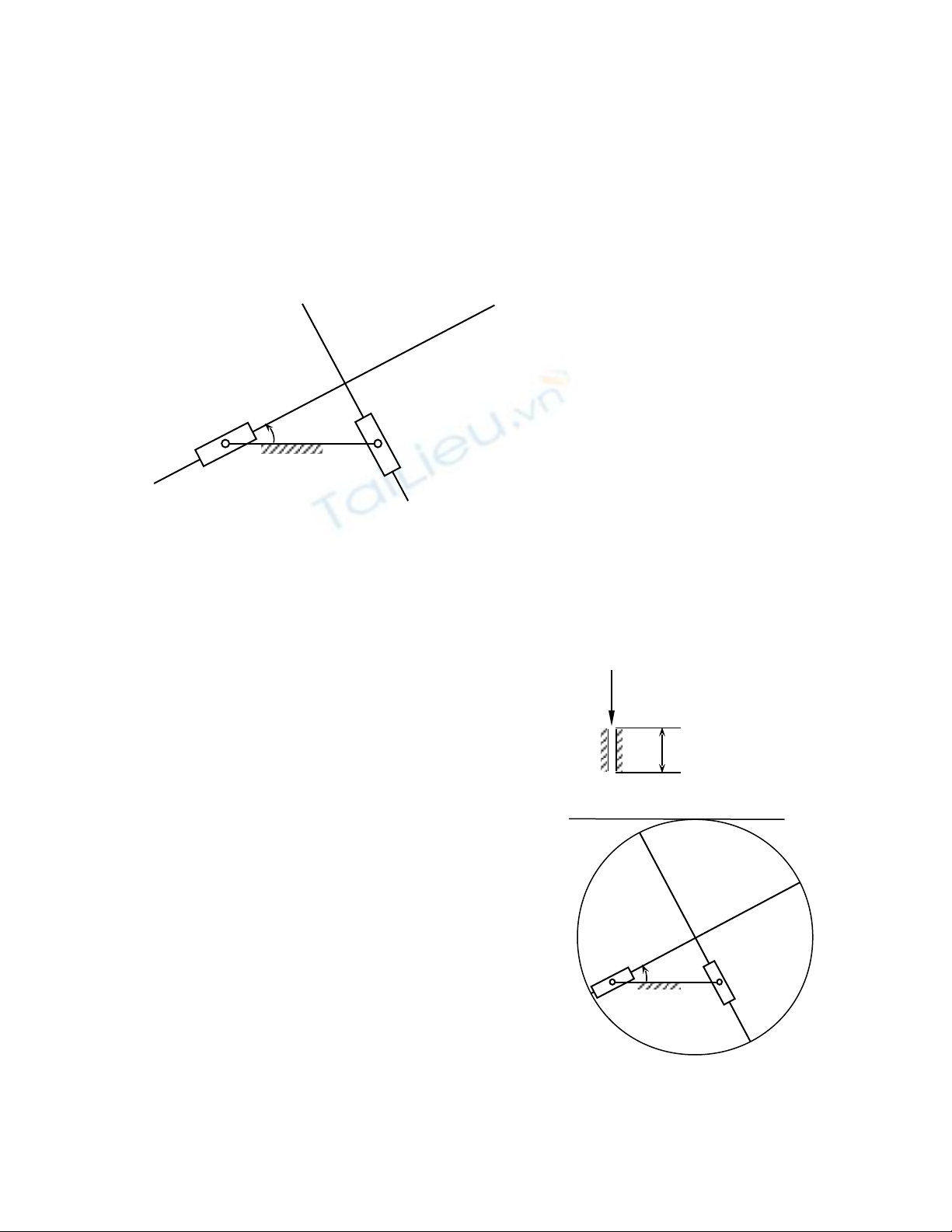
Hình 1 là c c u ph ngơ ấ ẳ
Onđam truy n chuy n đ ngề ể ộ
quay gi a hai con tr t 1,3. Haiữ ượ
con tr t này n i v i giá 4 b ngượ ố ớ ằ
hai kh p quay ớA(1,4), B(4,3) có
kho ng cách ảAB = d bi n đ iế ổ
trong kho ng 3cm ả≤ d ≤ 4cm,
đ ng th i n i v i thanh truy nồ ờ ố ớ ề
2 (khâu ch th p) b ng haiữ ậ ằ
kh p tr t ớ ượ A(1,2) và B(2,3) có
ph ng vuông góc t i ươ ạ C.
1. V i ớω1 = const, hãy :
a. D ng l c đ đ ng c a c c u;ự ượ ồ ộ ủ ơ ấ
b. V ẽquĩ đ o, h a đ v n t c và gia t c c a đi m ạ ọ ồ ậ ố ố ủ ể E trên khâu 2 (là
đi m đ i x ng v i ể ố ứ ớ A qua C khi φ = 0);
c. Mô ph ng chuy n đ ng c a cỏ ể ộ ủ ơ
c u.ấ
2. Gi th ả ử g n c ngắ ứ v i khâu ch th p 2ớ ữ ậ
m t đĩa tròn (hình 2) có tâm ộC và bán kính
r2 = 4cm, đ t o thành m t c c u camể ạ ộ ơ ấ
ph ng v i c n đáy b ng 5, t nh ti n theoẳ ớ ầ ằ ị ế
kh p tr t ớ ượ K(4,5) vuông góc v i ớAB t iạ
A. Khi d bi n đ i t 4cm t i 3cm, hãy :ế ổ ừ ớ
a. D ng l c đ đ ng c a c c u;ự ượ ồ ộ ủ ơ ấ
b. V h a đ v n t c và gia t c c aẽ ọ ồ ậ ố ố ủ
c n đ y;ầ ẩ
c. Mô ph ng chuy n đ ng c a cỏ ể ộ ủ ơ
c u.ấ
1
AB
C
E
φ
2
3
1
4
d
Hình 1
AB
C
E
φ
2
3
1
d
T
4
5
Ka
Q
Hình 2
3. Thay c c u Onđam đã cho b ng c c u tâm tích (hình thành t tâmơ ấ ằ ơ ấ ừ
v n t c t c th i ậ ố ứ ờ P24) th c hi n chuy n đ ng c a c c u cam trên đây.ự ệ ể ộ ủ ơ ấ
4. Ch n ph ng án c u t o 3D ọ ươ ấ ạ kh thiả cho các khâu trong các c c u 1, 2ơ ấ
và 3 trên đây (v i c c u 3, t ng ng v i c p tâm tích là c p bánh maớ ơ ấ ươ ứ ớ ặ ặ
sát và c p bánh răng th ng). L p và ặ ẳ ắ mô ph ng 3Dỏ các c c u đó.ơ ấ
2