Trang1/7-Mãđềthi147
TRƯỜNGTHPT………….
TỔ TOÁN
BÀI:………………….
NĂM HỌC 2018 – 2019
Môn: Toán - Lớp 11 - Chương trình chuẩn
ĐỀ CHÍNH THỨC Thời gian: ……… phút
Mã đề thi
147
Họ và tên:
………………………………………….
Lớp:
……………...……..………
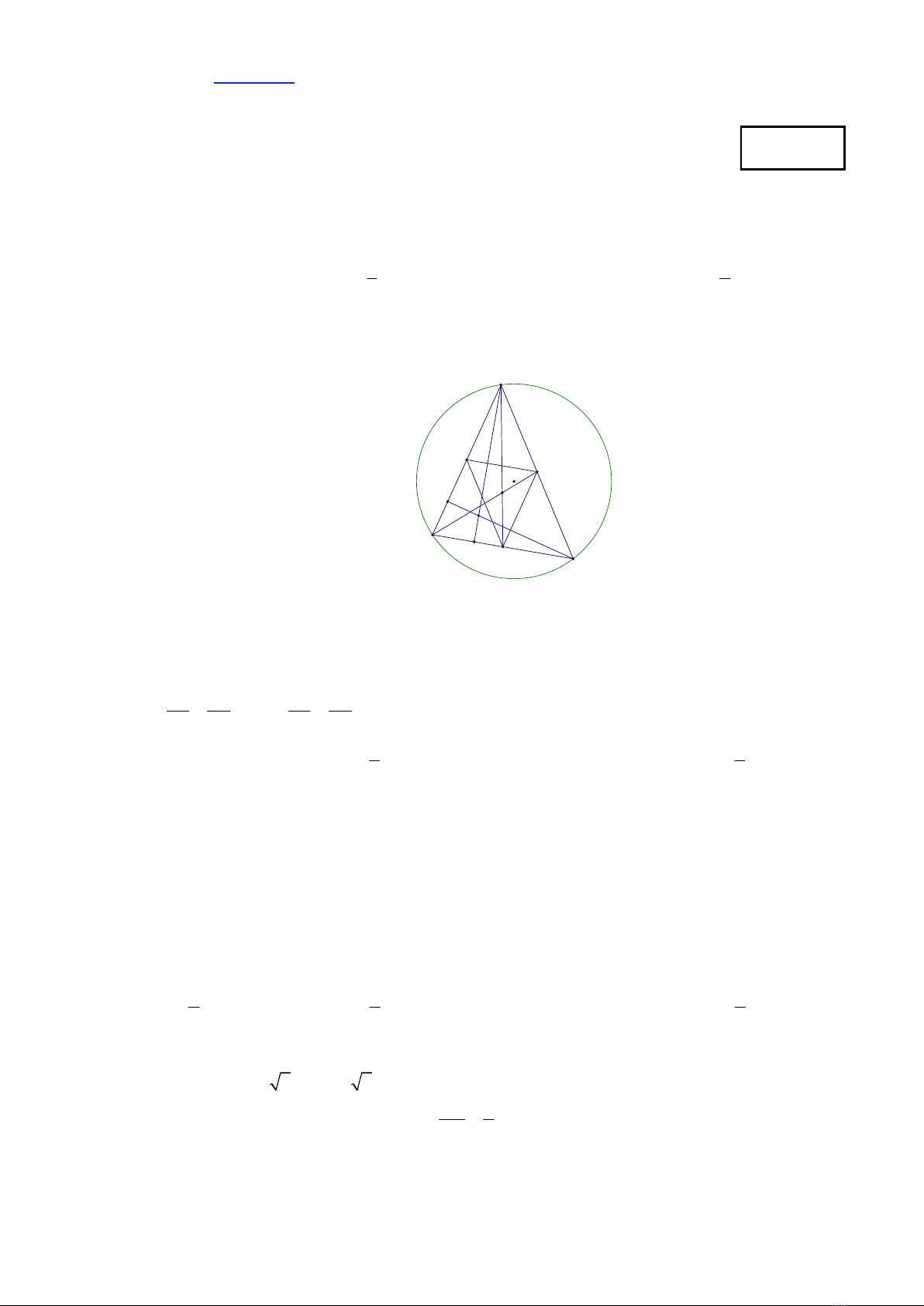
Câu 1. Cho tam giác
ABC
với
G
là trọng tâm, trực tâm
H
và tâm đường tròn ngoại tiếp
O
. Gọi
, ,
ABC
lầnlượtlàtrungđiểmcáccạnh
, ,BC CA AB
củatamgiác
ABC
. Hỏiquaphépbiếnhình
nàothìđiểm
O
biếnthànhđiểm
H
?
A. Phéptịnhtiếntheovectơ 1
. B. Phépvịtựtâm
G
,tỉsố
1
2
.
C. Phépvịtựtâm
G
,tỉsố
–2
. D. Phépquaytâm
O
,gócquay
60
.
Lờigiải
Chọn C
Tacó ,
OA BC BC B C OA B C
dođótacó
O
chínhlàtrựctâmcủatamgiác
A B C
.
Vìphépvịtựtâm
G
tỉsố
2
biếntamgiác
, ,
ABC
thành
ABC
nênsẽbiếntrựctâmtamgiác
nàythànhtamgiáckia,tứclà
O
biếnthànhđiểm
H
.
Câu 2. TrongmặtphẳngvớihệtrụctọađộOxy,chohaiElip
1
E
và
2
E
lầnlượtcóphươngtrìnhlà:
và .Khiđó
2
E
làảnhcủa
1
E
quaphépđồngdạngtỉsố
k
bằng:
A.
1
k
B. C. D.
Lờigiải
Chọn A
1
E
cótrụclớn 1 2
3
B B
2
E
cótrụclớn 1 2
3
A A
2
E
làảnhcủa
1
E
quaphépđồngdạngtỉsố
k
thì 1 2 1 2
. 3 3 1A A k B B k k
Câu 3. TrongmặtphẳngvớihệtọađộOxy,chobốnđiểm
2;1 , 0;3 ,
A B
1; 3 ,
C
2;4
D.Nếucó
phépđồngdạngbiếnđoạnthẳng
AB
thànhđoạnthẳng
CD
thìtỉsố
k
củaphépđồngdạngđó
bằng:
A.
5
2
B.
7
2
C.
2
D.
3
2
Lờigiải
Chọn A
Tacó:.
2 2, 5 2
AB CD
Suyratỉsốcủaphépđồngdạnglà
5
2
CD
k
AB
.
H
K
N
G
C'
B'
A'
O
C
A
B
1
95
22 yx 1
59
22 yx
5
9
1k
9
5
Trang2/7-Mãđềthi147
Câu 4. Cácphépbiếnhìnhbiếnđườngthẳngthànhđườngthẳngsongsonghoặctrùngvớinócóthểkểra
là:
A. Phépdờidình,phépvịtự. B. Phépvịtự.
C. Phépđồngdạng,phépvịtự. D. Phépđồngdạng,phépdờihình,phépvịtự.
Lờigiải
Chọn B
Giảsửđườngthẳng
: 0
d ax by c
(với 2 2
0
a b
)cóvéctơchỉphương
(a;b)
v
Gọi ( ; )
M x y d
,
0 0
( ; )I x y

M
làảnhcủa
M
qua
;V I k
khiđó
0
0
0 0
kx
( )
k(y y ) y ky
x
x
x k x x k
IM kIM yyk
Do
M d
nên 0 0 0 0
kx y ky
0 0
xa b
a b c x y c ax by
k k k k
Nênphươngtrìnhảnh
d
cóvéctơchỉphương
;v k a b
dođó
d
và
d
songsonghoặctrùng
nhau.
Chúý:loạiphépdờihìnhvàphépđồngdạngvìphépquaycũnglàphépdờihìnhvàđồngdạng
Câu 5. Mọiphépdờihìnhcũnglàphépđồngdạngtỉsố
A.
3
k
. B.
–1
k
. C.
0
k
. D.
1
k
.
Lờigiải
Chọn D
Theotínhchấtcủaphépđồngdạng.
Câu 6. TrongmặtphẳngvớihệtrụctọađộOxycho
–2; – 3 , 4;1 .
A B Phépđồngdạngtỉsố
1
2
k
biến
điểm
A
thành
,A
biếnđiểm
B
thành
.B
Khiđóđộdài
A B
là:
A. B. C. D.
Lờigiải
Chọn C
Vìphépđồngdạngtỉsố
1
2
k
biếnđiểm
A
thành
,A
biếnđiểm
B
thành
B
nên
2 2
1 1
4 2 1 3 52
2 2
A B AB
Câu 7. Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường tròn:
2 2
: 2 2 2 0
C x y x y
,
2 2
D : 12 16 0
x y x y
.Nếucóphépđồngdạngbiếnđườngtròn
C
thànhđườngtròn
D
thìtỉsố
k
củaphépđồngdạngđóbằng:
A.
2.
B.
3
C.
4
D.
5
Lờigiải
Chọn D
+Phươngtrìnhcủa
2 2
: 2 2 2 0
C x y x y
cótâm
1;1
I,bánkính.
2R
+Phươngtrìnhcủa
2 2
D : 12 16 0
x y x y
D
cótâm
( 6;8)
J
,bánkính
10
r
Tỉsốcủaphépđồngdạnglà
5
r
k
R
Câu 8. Chohìnhvẽsau:
50
2
52 52
2
50
Trang3/7-Mãđềthi147
Hình 1.88
XétphépđồngdạngbiếnhìnhthangHICDthànhhìnhthangLJIK.Tìmkhẳngđịnhđúng:
A. Phépđốixứngtâm
I
Ñvàphépvịtự
1
C,2
V
B. Phéptịnhtiến
AB
T
vàphépvịtự
,2I
V
C. Phépđốixứngtrục
BD
Ñvàphépvịtự
B, 2
V
D. Phépđốixứngtrục
AC
Ñvàphépvịtự
B,2
V
Lờigiải
Chọn A
Tacó:
I
Ñ : HICD KIAB;
1
C,2
V :KIAB LJIK
DođótachọnđápánB
Câu 9. Chohaidiểm
, A B
phânbiệt.Hãychọnmệnhđềsai.
A. Códuynhấtphépđốixứngtrụcbiếnđiểm
A
thành
.B
B. Códuynhấtphépđốixứngtâmbiếnđiểm
A
thành
.B
C. Códuynhấtphéptịnhtiếnbiếnđiểm
A
thành
.B
D. Códuynhấtphépvịtựbiếnđiểm
A
thành
.B
Lờigiải
Chọn D
Códuynhấtphépđốixứngtrục
d
biếnđiểm
A
thành
B
với
d
làtrungtrực
AB
(mỗiđoạncóduy
nhấtmộttrungtrực)
Códuynhấtphépđốixứngtâm
I
biếnđiểm
A
thành
B
(
AB
códuynhấtmộttrungđiểm
I
)
Códuynhấtphéptịnhtiếnbiếnđiểm
A
thành
B
(vì
AB

làduynhấtvới
,A B
cốđịnhchotrước)
Phépvịtự
;V I k A B IB kIA
dođóứngvớimỗitâmvịtự
I
vàmộttỉsố
k
chotamột
phépvịtựdođócóvôsốphépvịtự.
Câu 10. Trong mặt phẳng
Oxy
cho đường tròn
2 2
: 6 4 23 0C x y x y
, tìm phương trình đường
tròn
C
làảnhcủađườngtròn
C
quaphépđồngdạngcóđượcbằngcáchthựchiệnliêntiếp
phéptịnhtiếntheovectơ
3;5v
vàphépvịtự
1
;3
.
O
V
A.
2 2
' : 2 1 2.C x y
B.
2 2
' : 2 1 4.C x y
C.
2 2
' : 2 1 36.C x y
D.
2 2
' : 2 1 6.C x y
Lờigiải
Chọn B
Đườngtròn
C
cótâm
3; 2I
vàbánkính
9 4 23 6.R
.
1
;3
3;5
3; 2 ' 6;3 '' 2; 1 .
O
v
V
T
v
I I I
Trang4/7-Mãđềthi147
1
' 2.
3
R R
Vậy
2 2
: 2 1 4.
C x y
Câu 11. Trongmặtphẳngvớihệtrụctọađộ
Oxy
,chođiểm
1;1
Ivàđườngtròn
C
cótâm
I
bánkính
bằng
2
.Gọiđườngtròn
C
làảnhcủađườngtròntrênquaphépđồngdạngcóđượcbằngcách
thựchiệnliêntiếpphépquaytâm
O
,góc
45
vàphépvịtựtâm
O
,tỉsố
2
.Tìmphươngtrình
củađườngtròn
C
?
A.
2 2
1 1 8
x y
. B.
2
2
1 8
x y
.
C.
2
2
2 8
x y
. D.
22
2 8
x y
.
Lờigiải
Chọn C
Đườngtròn
C
cótâm
(1;1)I
,bánkínhbằng
2
.
Gọi
( ; )
J J
J x y
làảnhcủa
(1;1)I
quaphépquaytâm
O
gócquay
45
.
Ta có:
1.cos 45 1.sin 45 0
1.cos 45 1.sin 45 2
J
J
x
y
. (công thức này không có trong SGK cơ bản, nếu sử
dụngphảichứngminhchohs)
Phươngtrìnhcủaảnhcủađườngtrònquaphépquaytrênlà:
2
2
2 4
x y
.
Gọi
( ; )
K K
K x y
làảnhcủa
J
quaphépvịtựtâm
O
tỉsố
2
.
Tacó:
2.0 0
2. 2 2
K
K
x
y
.Bánkínhcủađườngtrònquaphépvịtựnàybằng
2 2
.
Phươngtrìnhcủaảnhcủađườngtrònquaphépvịtựtrênlà
2
2
2 8
x y
.
Câu 12. TrongmặtphẳngvớihệtrụctọađộOxychođườngthẳng
: – 2 1 0
d x y
,Phépvịtựtâm
0;1
Itỉ
số
–2
k
biếnđườngthẳngd thànhđườngthẳng
d
,phépđốixứngtrụcOxbiếnđườngthẳng
d
thànhđườngthẳng
1
d
.Khiđóphépđồngdạngbiếnđườngthẳngdthành
1
d
cóphươngtrìnhlà:
A.
2 – 4 0
x y
B.
2 4 0
x y
C.
– 2 8 0
x y
D.
2 4 0
x y
Lờigiải
Chọn C
Gọi
;
M x y d
,
x ; y
M
làảnhcủa
M
qua
; 2
V I
Tacó:
0 2 0
3
2
2 ;
32 2
1 2 1
2
x
x
x x x y
IM IM M
y
y y y
Vì
;
M x y d
nên: – 2 1 0 2
3
2
8 0
2
x y x y
Vậy
:x 2 y 8 0
d
Câu 13. Trongmătphẳng
Oxy
chođiểm
2;4 .
MPhépđồngdạngcóđượcbằngcáchthựchiệnliêntiếp
phépvịtựtâm
O
tỉsố
1
2
k
vàphépđốixứngquatrục
Oy
sẽbiến
M
thànhđiểmnàotrongcác
điểmsau?
A.
1;2 .
B.
1; 2 .
C.
1;2 .
D.
2;4 .
Trang5/7-Mãđềthi147
Lờigiải
Chọn A
Tacó:
1 1
, ;
2 2
; .
Oy
O O
M V M M D V M
Tọađộđiểm
M
là:
1 1
2. 1 0
1
2 2
.
2
1 1
4. 1 0
2 2
xx
y
y
Tọađộđiểm
M
là:
1.
2
x x x
y y y
Câu 14. Trongcácmệnhđềsau,mệnhđềnàosai?
A. Phépquaylàmộtphépđồngdạng. B. Phépđồngdạnglàmộtphépdờihình.
C. Phépdờihìnhlàmộtphépđồngdạng. D. Phépvịtựlàmộtphépđồngdạng.
Lời giải
Chọn B
Phépdờihìnhlàmộtphépđồngdạngvớitỉsốđồngdạngbằng
1
,điềungượclạikhôngđúng.
Câu 15. Trongmătphẳng
Oxy
chođườngthẳngdcóphươngtrình
2 0.
x y
Phépđồngdạngcóđược
bằngcáchthựchiệnliêntiếpphépvịtựtâm
O
tỉsố
2
k
vàphépđốixứngquatrục
Oy
sẽbiến
d
thànhđườngthẳngnàotrongcácđườngthẳngsau?
A.
2 0.
x y
B.
2 0.
x y
C.
4 0.
x y
D.
2 2 0.
x y
Lờigiải
Chọn B
TâmvịtựO thuộcđườngthẳng
d
nên ( ; 2)
( )
O
d V d
.
( )
Oy
d D d
cóphươngtrìnhlà:
.
x x x x
y y y y
Mà
2 0 2 0 2 0.
x y x y x y
Câu 16. Tìmmệnhđềsaitrongcácmệnhđềsau:
A. Cómộtphéptịnhtiếnbiếnmỗiđiểmtrongmặtphẳngthànhchínhnó.
B. Cómộtphépquaybiếnmỗiđiểmtrongmặtphẳngthànhchínhnó.
C. Cómộtphépvịtựbiếnmỗiđiểmtrongmặtphẳngthànhchínhnó.
D. Cómộtphépđốixứngtrụcbiếnmỗiđiểmtrongmặtphẳngthànhchínhnó.
Lờigiải
Chọn D
Chỉcónhữngđiểmtrêntrụcđốixứngmớibiếnthànhchínhnó.
Câu 17. TrongmặtphẳngvớihệtrụctọađộOxy,chođườngtròn(C)tâm
,3;2
Ibánkính
2R
.Gọi
'C
làảnhcủa
C
quaphépđồngdạngtỉsố
3
k
.Khiđótrongcácmệnhđềsaumệnhđềnào
sai ?
A.
C
cóphươngtrình
2 2
– 3 – 2 36
x y
. B.
C
cóphươngtrình 2 2
– 2 – 35 0
x y y
.
C.
C
cóphươngtrình 2 2
2 – 36 0
x y x
. D.
C
cóbánkínhbằng6.
Lờigiải
Chọn C
Tacó
C
làảnhcủa
C
quaphépđồngdạngtỉsố
3
k
thì
C
cóbánkính
3 6
R R
Màphươngtrình 2 2
( ) : 2 – 36 0
C x y x
cóbánkính
37
RnênđápánCsai