Trang 1/8 - Mã đề thi 147
TRƯỜNG THPT ………….
TỔ TOÁN
BÀI:………………….
NĂM HỌC 2018 – 2019
Môn: Toán - Lớp 11 - Chương trình chuẩn
ĐỀ CHÍNH THỨC Thời gian: ……… phút
Mã đề thi
147
Họ và tên:
………………………………………….
Lớp:
……………...……..………
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt
phẳng đáy,
SA a
. Gọi M là trung điểm của CD. Khoảng cách từ M đến mặt phẳng
SAB
nhận
giá trị nào sau đây?
A.
2a
B.
2a
C.
2
2
a
D.
a
Lời giải
Chọn D
Ta có:
/ / , ,AB CD d M SAB d D SAB
Mặt khác
AD AB AD SAB
AD SA
Do vậy
,d M SAB AD a
.
Câu 2. Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc nhau và
SA SB SC a
. Khi đó
khoảng cách từ S đến mặt phẳng
ABC
bằng:
A.
3
a
B.
2
a
C.
3
a
D.
2
a
Lời giải
Chọn C
Gọi
2 2 2 2 2
1 1 1 1 3
,3
a
h d S ABC h
h SA SB SC a
.
Câu 3. Cho hình chóp
ABCDS.
có đáy
ABCD
là hình chữ nhật tâm
I
, cạnh bên
SA
vuông góc với đáy.
KH,
lần lượt là hình chiếu của
A
lên SDSC,. Kí hiệu
( ,( ))d A SCD
là khoảng cách giữa điểm A
và mặt phẳng
( )SCD
. Khẳng định nào sau đây đúng?
A.
( ,( ))d A SCD AH
. B.
( ,( ))d A SCD AD
.
C.
( ,( ))d A SCD AC
. D.
( ,( ))d A SCD AK
.
Lời giải:
Chọn D
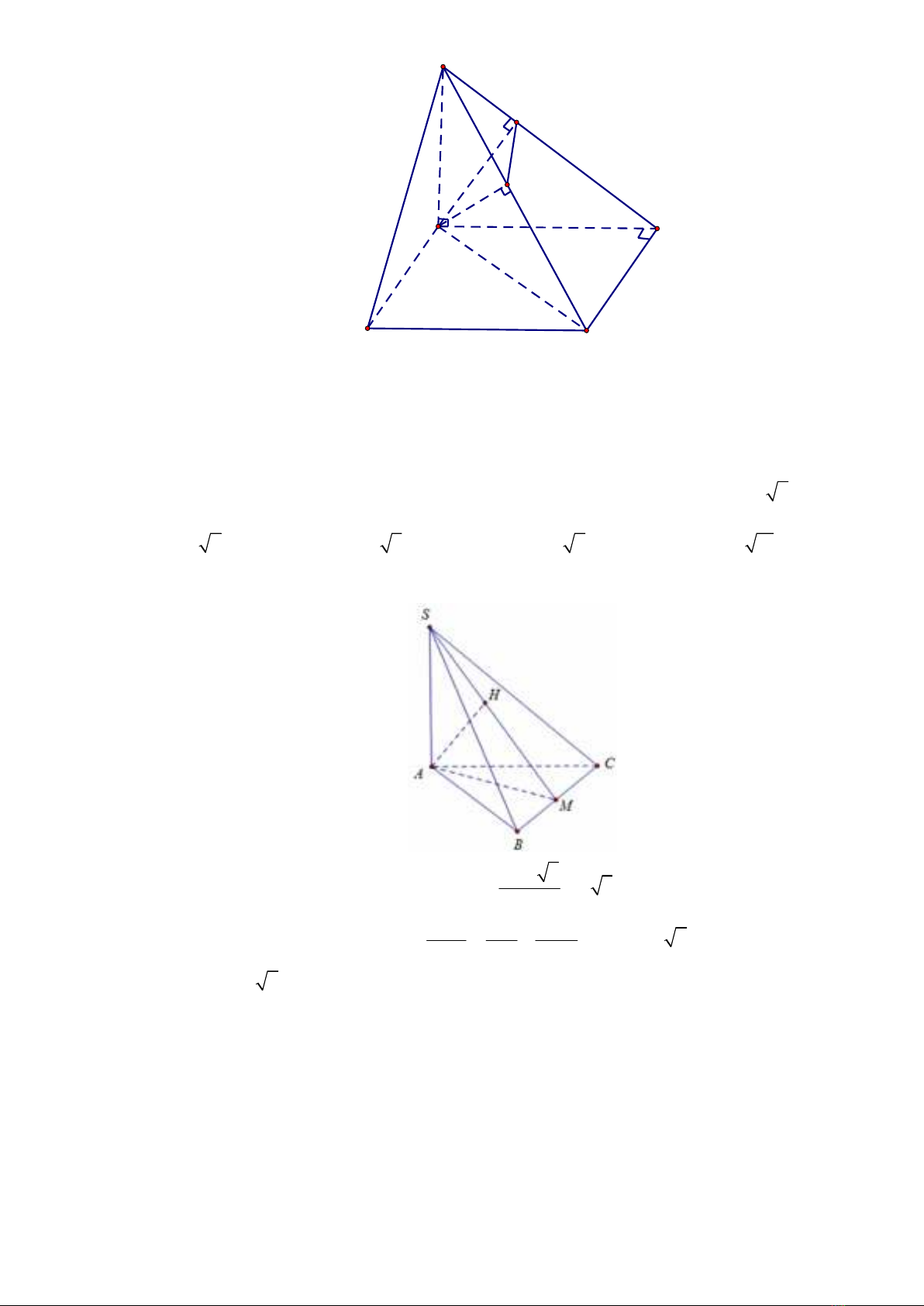
Trang 2/8 - Mã đề thi 147
Ta có:
1AK SD
2
SA CD CD SAD CD AK
AD CD
Từ (1) và (2)
AK SCD
. Hay
,AK d A SCD
.
Câu 4. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a,
SA ABC
và
6SA a
. Gọi M là
trung điểm của BC, khi đó khoảng cách từ A đến đường thẳng SM bằng:
A.
2a
B.
3a
C.
6a
D.
11a
Lời giải
Chọn A
Dựng
2 3
, ; 3
2
a
AH SM d A SM AH AM a
Xét tam giác SAM vuông tại A ta có:
2 2 2
1 1 1 2AH a
AH SA AM
Do đó
2d a
.
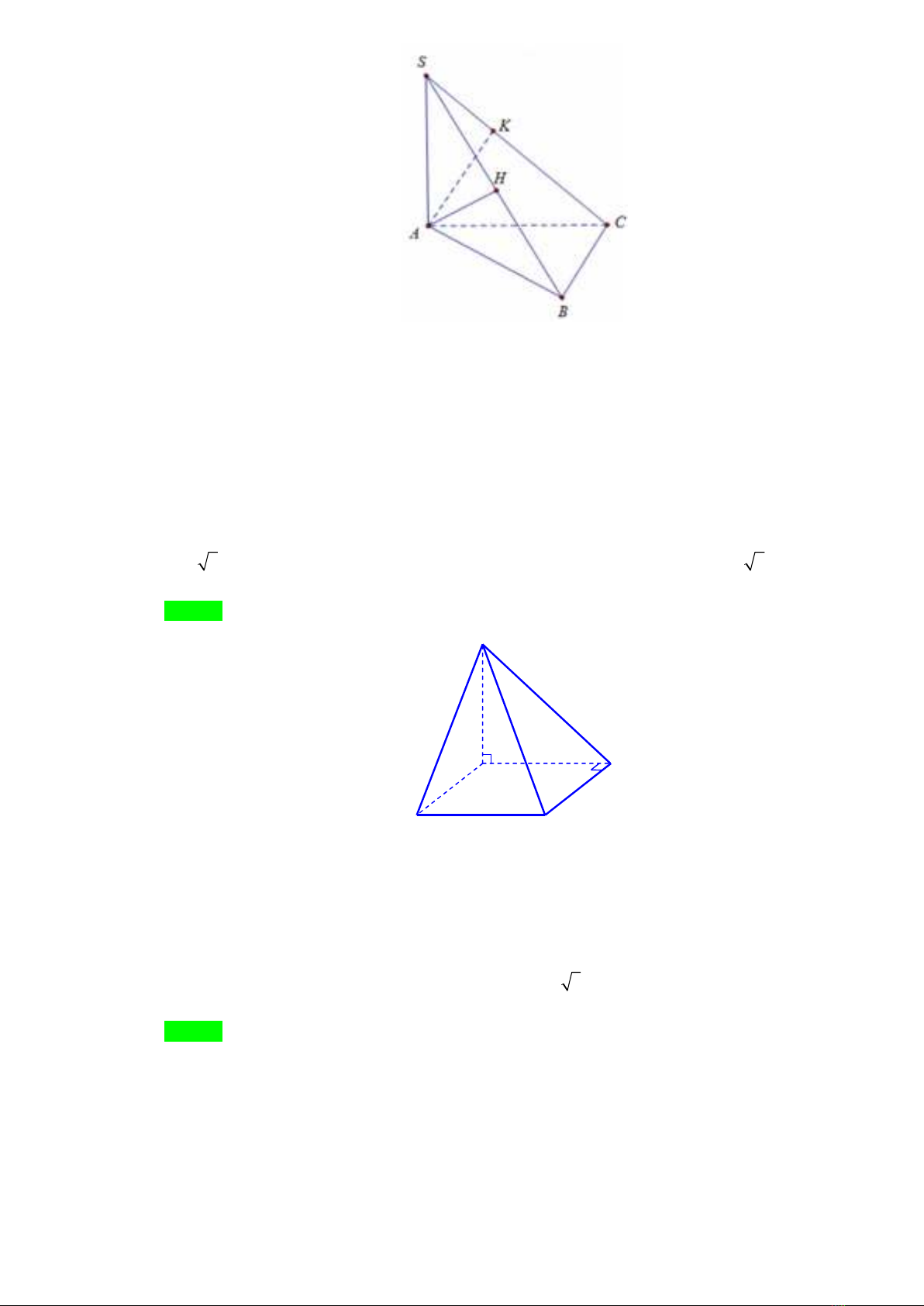
Câu 5. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với mặt phẳng
ABC
.
Gọi H và K lần lượt là hình chiếu của A lên SB và SC. Mệnh đề nào sau đây sai?
A.
,d S ABC SA
B.
,d A SBC AH
C.
,d A SBC AK
D.
,d C SAB BC
Lời giải
Chọn C
C
A
D
B
S
H
K
Trang 3/8 - Mã đề thi 147
Ta có:
,
BC AB BC SAB d C SAB BC
BC SA
.
Lại có:
,
BC AH AH SBC d A SBC AH
AH SB
Mặt khác
,SA ABC d S ABC SA
.
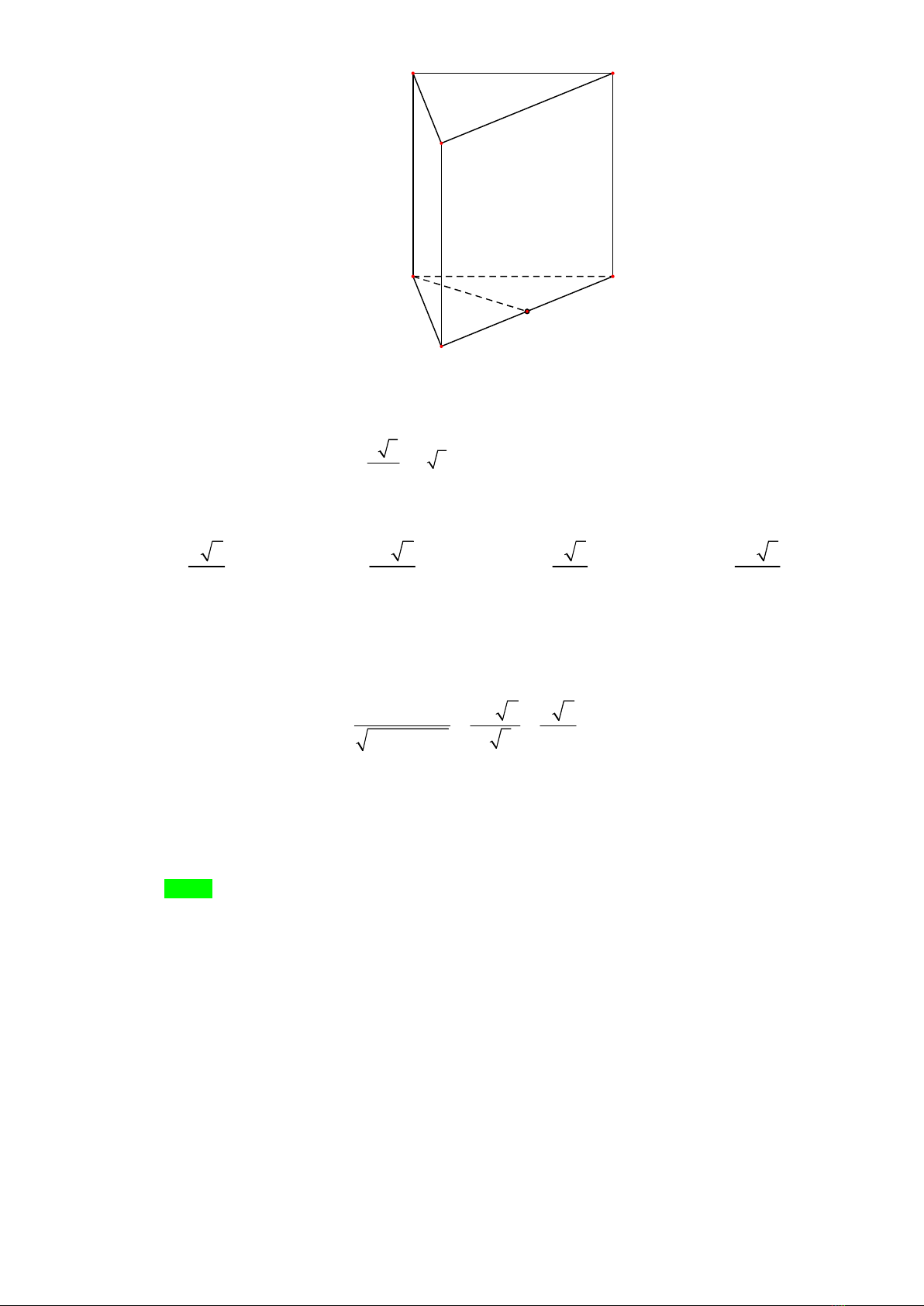
Câu 6. (Sở Giáo dục Gia Lai – 2018-BTN)Cho hình chóp
.S ABCD
có đáy là hình chữ nhật
AB a
,
2BC a
, cạnh bên
SA
vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng
SA
và
CD
.
A. 5a. B.
a
. C.
2a
. D. 6a.
Lời giải
Chọn C
Ta có AD SA AD
AD CD
là đoạn vuông góc chung của
AD
và
SA
.
Do đó
, 2d SA CD AD a .
Câu 7. (THPT Sơn Tây - Hà Nội - 2018 – BTN – 6ID – HDG) Đáy của hình lăng trụ đứng tam giác
.ABC A B C
là tam giác đều cạnh bằng
4
. Tính khoảng cách giữa hai đường thẳng
AA
và
BC
.
A.
4
B.
3
C. 2 3 D.
1
Lời giải
Chọn C
S
A
B
C
D
Trang 4/8 - Mã đề thi 147
Gọi
M
là trung điểm của
BC
. Khi đó
AM AA
tại
A
,
AM BC
tại
M
.
Do đó
AM
là đoạn vuông góc chung giữa
AA
và
BC
,
suy ra
,
d AA BC AM
4 3
2 3
2
.
Câu 8. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, biết
2 2SA AC a
và SA vuông
góc với mặt phẳng đáy. Khoảng cách từ điểm A đến mặt phẳng
SBC
bằng:
A.
6
3
a B.
2 6
3
a C.
3
3
a
D.
4 3
3
a
Lời giải
Chọn A
Ta có
SA BC
BC SAB
AB BC
, kẻ
AH SB AH SBC
.
2 2
. . 2 6
,
3
3
SA AB a a a
d A SBC AH a
SA AB
.
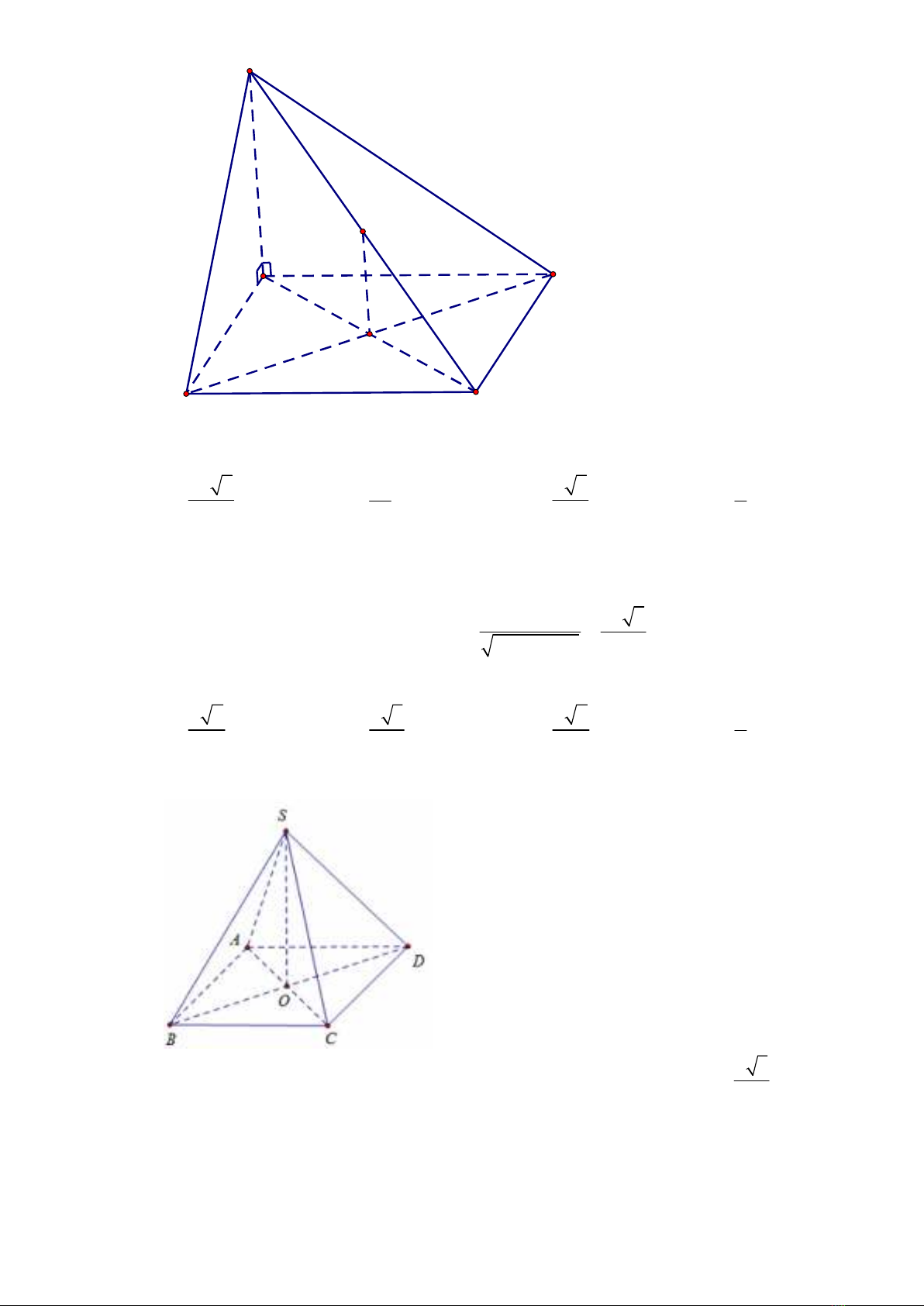
Câu 9. (THPT Lê Quý Đôn - Hà Nội - 2017 - 2018 - BTN) [1D3-1] Cho hình chóp .
S ABCD
có đáy
ABCD
là hình
vuông tâm
O
,
SA ABCD
. Gọi
I
là trung điểm của
SC
. Khoảng cách từ
I
đến mặt phẳng
ABCD
bằng độ dài đoạn thẳng nào?
A.
IB
. B.
IA
. C.
IC
. D.
IO
.
Lời giải
Chọn D
Do
I
là trung điểm của
SC
và
O
là trung điểm
AC
nên
//IO SA
. Do
SA ABCD
nên
IO ABCD
, hay khoảng cách từ
I
đến mặt phẳng
ABCD
bằng độ dài đoạn thẳng
IO
.
M
C
A
C'
A'
B'
B
Trang 5/8 - Mã đề thi 147
Câu 10. Cho hình chóp S.ABC có đáy ABC là tam giac vuông tại B với
AB a
,
2BC a
và
SA ABC
. Khoảng cách từ B đến mặt phẳng
SAC
bằng:
A.
2 5
5
a
B.
2
5
a
C.
5
5
a
D.
5
a
Lời giải
Chọn A
Kẻ
BH AC H AC
mà
SA ABC SA BH
2 2
. 2 5
,5
AB BC a
BH SAC d B SAC BH AB BC
.
Câu 11. Cho hình lăng trụ
. ' ' 'ABC A B C
có cạnh đáy bằng
a
và
'AA a
. Khoảng cách giữa
'AB
và
'CC
:
A.
2
2
a
B.
3
2
a
C.
2
3
a
D.
2
a
Lời giải
Chọn B
Ta có
3
', ' ', ' ' , ' ' , 2
a
d AB CC d CC ABB A d C ABB A d C AB
O
I
C
A
B
D
S


























