Đ s 9ề ố
Đ THI H C KÌ 1 – Năm h c 2010 – 2011Ề Ọ ọ
Môn TOÁN L p 11 Nâng caoớ
Th i gian làm bài 120 phútờ
Câu 1: (4 đi m)ể
1) Tìm giá tr l n nh t và giá tr nh nh t (n u có) c a hàm s ị ớ ấ ị ỏ ấ ế ủ ố
y x xsin2 3cos2 3= − +
.
2) Xét tính ch n, l và v đ th c a hàm s ẵ ẻ ẽ ồ ị ủ ố
y xsin 2= −
.
3) Gi i các ph ng trình sau:ả ươ
a)
x x
x
cos2 3cos 2 0
2sin 3
+ + =
−
b)
x x x x
2 2
sin sin cos 4cos 1 0+ − + =
c)
x x x
2
cos2 cos (2tan 1) 0+ − =
Câu 2: (3 đi m)ể
1) Xác đ nh h s c a ị ệ ố ủ
x3
trong khai tri n ể
x6
(2 3)−
.
2) M t t có 9 h c sinh, g m 5 nam và 4 n .ộ ổ ọ ồ ữ
a) Có bao nhiêu cách x p 9 h c sinh đó vào m t dãy bàn có 9 gh sao cho các h c sinh n luônế ọ ộ ế ọ ữ
ng i c nh nhau.ồ ạ
b) Ch n ng u nhiên 2 h c sinh. Tính xác su t đ :ọ ẫ ọ ấ ể
i) Trong 2 h c sinh đ c ch n có 1 nam và 1 n .ọ ượ ọ ữ
ii) M t trong 2 h c sinh đ c ch n là An ho c Bình.ộ ọ ượ ọ ặ
Câu 3: (1,5 đi m) ể
1) Cho đ ng tròn (C): ườ
và đi m I(–3; 2). Vi t ph ng trình đ ng tròn (Cể ế ươ ườ ′)
là nh c a (C) qua phép v t tâm I t s ả ủ ị ự ỉ ố
k2
= −
.
2) Cho tam giác đ u ABC. G i M, N l n l t là trung đi m c a AB, AC. Xác đ nh tâm và góc c aề ọ ầ ượ ể ủ ị ủ
phép quay bi n vect ế ơ
AM
uuur
thành vect ơ
CN
uuur
.
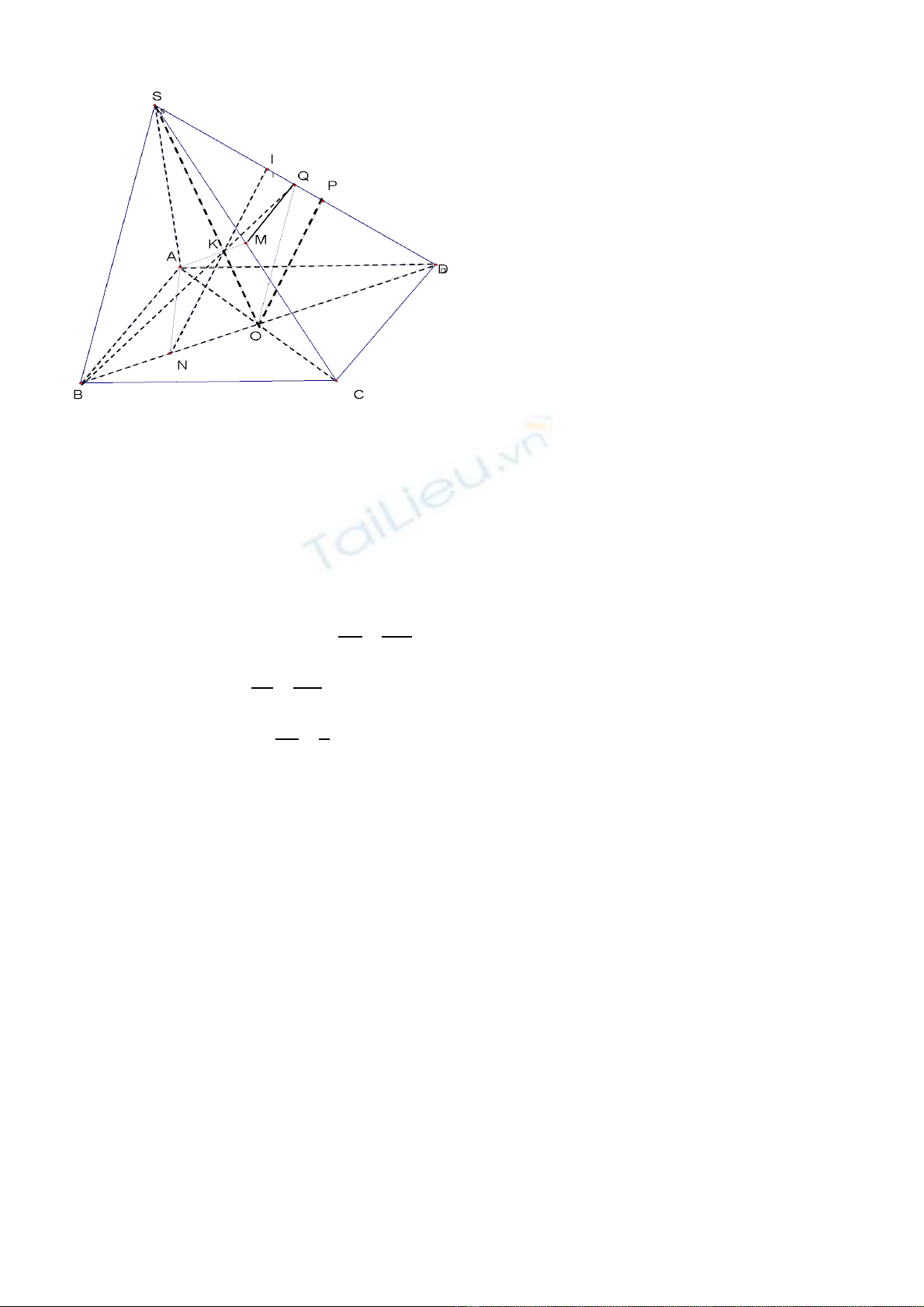
Câu 4: (1,5 đi m) Cho hình chóp S.ABCD, đáy là hình bình hành ABCD có tâm là O. G i M là trungể ọ
đi m c a SC.ể ủ
1) Xác đ nh giao tuy n c a (ABM) và (SCD).ị ế ủ
2) G i N là trung đi m c a BO. Hãy xác đ nh giao đi m I c a (AMN) v i SD. Ch ng minh r ngọ ể ủ ị ể ủ ớ ứ ằ
SI
ID
2
3
=
.
--------------------H t-------------------ế
H và tên thí sinhọ: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
1
Đ s 9ề ố
ĐÁP ÁN Đ THI H C KÌ 1 – Năm h c 2010 – 2011Ề Ọ ọ
Môn TOÁN L p 11 Nâng caoớ
Th i gian làm bài 120 phútờ
Câu 1: (4 đi m)ể
1) Giá tr l n nh t, giá tr nh nh t c a hàm s ị ớ ấ ị ỏ ấ ủ ố
y x xsin2 3cos2 3= − +
Ta có:
y x xsin2 3cos2 3= − +
=
x x
1 3
2 sin2 cos2 3
2 2
� �
− +
� �
� �
=
x2sin 2 3
3
π
� �
− +
� �
� �
⇒
y1 5
(vì
x1 sin 2 1
3
π
� �
− −
� �
� �
)
⇒
ymin 1=
khi
x k
12
ππ
= − +
;
ymax 5=
khi
x k
5
12
ππ
= +
.
2) Xét tính ch n, l c a hàm s ẵ ẻ ủ ố
y f x x( ) sin 2= = −
T p xác đ nh: D = Rậ ị
V i ớ
x2
π
=
, ta có:
fsin 2 1
2 2
π π
� �
= − = −
� �
� �
,
fsin 2 3
2 2
π π
� � � �
− = − − = −
� � � �
� � � �
⇒
f f
2 2
π π
� � � �
−
� � � �
� � � �
⇒ hàm s đã cho không là hàm s ch n cũng không là hàm s l .ố ố ẵ ố ẻ
3) Gi i ph ng trìnhả ươ
a)
x x
x
cos2 3cos 2 0
2sin 3
+ + =
−
. Đi u ki n: ề ệ
x x
2
3 1
sin cos
2 4
�۹
(*)
Khi đó PT ⇔
x
x x x x k k Z
x loai�
2cos 1
2cos 3cos 1 0 cos 1 2 ,
1
cos ( )
2
π π
= −
+ + = = − = +�� � �
= −
b)
x x x x x x x x
2 2 2 2
sin sin cos 4cos 1 0 2sin sin cos 3cos 0+ − + = + − =�
+ D th y cosễ ấ x = 0 không th a mãn ph ng trình đã choỏ ươ
+ V i cosớx ≠ 0, ta có:
PT ⇔
x x
2
2tan tan 3 0+ − =
x k
x
xx k
tan 1 4
33
tan arctan
22
ππ
π
= +
=
� � � �
= −
= − +
� �
� �
c)
x x x
2
cos2 cos (2tan 1) 0+ − =
. Đi u ki n cosề ệ x
0 (*)
Khi đó: PT ⇔
x
x x x x x
x
2
2 3 2
(1 cos )
2cos 2 cos 1 0 2cos 3cos cos 2 0
cos
−
+ − − = − − + =�
x
x x x x
2cos 1
(cos 1)(2cos cos 2) 0 1 17
cos 4
=
− − − =� � −
=
(tho (*))ả
x k
x k
2
1 17
arccos 2
4
π
π
=
−
= +
. V y PT có nghi m: ậ ệ
x k x k
1 17
2 ; arccos 2
4
π π
−
= = +
Câu 2:
1)
x6
(2 3)−
S h ng th ố ạ ứ k + 1 là
k k k k k k k k k
k
T C x C x
6 6 6
1 6 6
( 1) (2 ) 3 ( 1) 2 3
− − −
+= − = −
Đ s h ng ch a ể ố ạ ứ
x3
thì
k k6 3 3
− = =�
. V y h s c a ậ ệ ố ủ
x3
là
C3 3 3
6.2 .3 4320− = −
2
2) a) G i 5 h c sinh nam là A, B, C, D, E. ọ ọ
Vì 4 h c sinh n luôn ng i g n nhau nên ta có 4! = 24 cách s p x p 4 h c sinh n .ọ ữ ồ ầ ắ ế ọ ữ
M t khác ta có th xem nhóm 4 h c sinh n này là F.ặ ể ọ ữ
S cách s p x p A, B, C, D, E, F là 6! = 720 (cách)ố ắ ế
V y có t t c : 24ậ ấ ả ×720 = 17280 (cách)
b) Ch n ng u nhiên 2 h c sinh trong 9 h c sinh có ọ ẫ ọ ọ
C2
936=
(cách) ⇒ Không gian m u cóẫ
n( ) 36
Ω
=
i) G i A là bi n c "trong 2 h c sinh đ c ch n có 1 nam và 1 n ". ọ ế ố ọ ượ ọ ữ
⇒ S cách ch n 2 h c sinh trong đó có 1 nam và 1 n là: ố ọ ọ ữ
n A C C
1 1
5 4
( ) . 5.4 20= = =
V y ậ
n A
P A n
( ) 20 5
( ) ( ) 36 9
Ω
= = =
ii) V n không gian m u trên nên ẫ ẫ
n( ) 36
Ω
=
G i B là bi n c m t trong hai h c sinh đ c ch n là An ho c Bình.ọ ế ố ộ ọ ượ ọ ặ
Gi s h c sinh th nh t đ c ch n là An ho c Bình ả ử ọ ứ ấ ượ ọ ặ ⇒ có 2 cách ch n h c sinh th nh t.ọ ọ ứ ấ
S cách ch n h c sinh còn l i là: ố ọ ọ ạ
C1
77=
(cách)
⇒
n B( ) 2.7 14= =
⇒
n B
P B n
( ) 14 7
( ) ( ) 36 18
Ω
= = =
Câu 3:
1) Xét phép v t ị ự
I
V( ; 2)−
.
M i đi m ỗ ể
M x y C( ; ) ( )
có nh là ả
M x y C'( '; ') ( )
x x x x
IM IM y y
y y
2 9 2 ' 9
' 2 2 ' 6
2 6
= − − = − −
= −� � �
� � = − +
= − +
uuur uuur
Ta có:
M x y C( ; ) ( )
⇔
⇔
x y x
2 2
(2 ) (2 ) 16(2 ) 24 0+ − + =
⇔
x y x
2 2
( ' 9) ( ' 6) 16( ' 9) 24 0− − + − + − − − + =
⇔
x y x y
2 2
( ') ( ') 34 ' 12 ' 285 0+ + − + =
⇔
M x y C'( '; ') ( )
V y ph ng trình đ ng tròn ậ ươ ườ
C x y x y
2 2
( ): 34 12 285 0
+ + − + =
Cách 2: Đ ng tròn (C): ườ
có tâm K(4; 0) và bán kính
R10=
G i ọ
K x y'( ; )
và R′ là tâm và bán kính c a đ ng tròn nh (Củ ườ ả ′).
⇒
I
K V I
( ; 2)( )
−
=
và
R R2 2 10
= =
.
Ta có:
x x K
y y
3 2(4 3) 17 ( 17;6)
2 2(0 2) 6
� �
+ = − + = − −� �
� �
− = − − =
� �
V y ph ng trình c a (Cậ ươ ủ ′) là
x y
2 2
( 17) ( 6) 40+ + − =
.
2)
G i O là tâm c a tam giác đ u ABC. ọ ủ ề
Ta có: OA = OC,
OA OC 0
( , ) 120= −
(ho c ặ
OA OC 0
( , ) 120=
)
và OM = ON,
OM ON 0
( , ) 120= −
(ho c ặ
OM ON 0
( , ) 120=
)
Do đó: phép quay
O
Q A C M N
0
( , 120 ) : ;
−
a a
hay
AM CN
uuur uuur
.
(ho c ặphép quay
O
Q A C M N
0
( ,120 ) : ;
a a
hay
AM CN
uuur uuur
).
3
A
BC
O
M N
0
120
Câu 4:
1) Giao tuy n c a (ABM) và (SCD).ế ủ
Ta có: M ∈ (ABM) ∩ (SCD). Gi s ả ử
ABM SCD Mx( ) ( ) =�
.
Vì (ABM) // CD nên Mx // CD. Trong (SCD), g i Q = Mọx ∩ SD. Suy ra MQ // CD ⇒ Q là trung
đi m c a SD.ể ủ
V y: ậ
ABM SCD MQ( ) ( ) =�
v i Q là trung đi m c a SD.ớ ể ủ
2) Giao đi m c a (AMN) v i SD.ể ủ ớ
Trong (SAC), g i K = AM ọ∩ SO ⇒ K ∈ (AMN) và K là tr ng tâm c a ọ ủ ∆SAC.
Trong (SBD), g i I = NK ọ∩ SD ⇒ I = (AMN) ∩ SD.
Trong ∆SBD, d ng OP//NI ự
DI DN DI PI
PI ON 3 3= = =� �
(1)
Trong ∆SOP, ta có
SI SK SI PI
PI OK 2 2= = =�
(2)
T (1) và (2) ta suy ra ừ
SI
DI
2
3
=
(đpcm).
============================
4