KY THI OLYMPIC TRUYÊN THÔNG 30/4
LÂN TH XIII TAI THANH PHÔ HUÊ Ư
ĐÊ THI MÔN V T LÝ 11 Ậ
Th i gian lam bai 180’ơ
Chu y: Môi câu hoi thi sinh lam trên 01 t giây riêng biêt ơ
( Đ thi có 02 trang)ề
Câu 1: (4 đi m) ể
M t t m ván dài kh i l ng M n m trên m tộ ấ ố ượ ằ ộ
m t ph ng nh n n m ngang không ma sát và đ c giặ ẳ ẵ ằ ượ ữ
b ng m t s i dây không giãn. M t v t nh kh i l ngằ ộ ợ ộ ậ ỏ ố ượ
m tr t đ u v i v n t c vượ ề ớ ậ ố 0 t mép t m ván d i tácừ ấ ướ
d ng c a m t l c không đ i F (hình v ). Khi v t điụ ủ ộ ự ổ ẽ ậ
đ c đo n đ ng dài ượ ạ ườ l trên t m ván thì dây b đ t.ấ ị ứ
a. Tính gia t c c a v t và t m ván ngay sau khi dây đ t.ố ủ ậ ấ ứ
b. Mô t chuy n đ ng c a v t và t m ván sau khi dây đ t trong m t th i gianả ể ộ ủ ậ ấ ứ ộ ờ
đ dài.Tính v n t c, gia t c c a v t và t m ván trong t ng giai đo n.ủ ậ ố ố ủ ậ ấ ừ ạ
c. Hãy xác đ nh chi u dài ng n nh t c a t m ván đ v t không tr t kh i t mị ề ắ ấ ủ ấ ể ậ ượ ỏ ấ
ván.
Câu 2 : (4 đi m)ể
Cho c h nh hình v . Qu c u đ c có ơ ệ ư ẽ ả ầ ặ kh i l ng m, bán kính r lăn khôngố ượ
tr t trong máng có bán kính R. Máng đ ng yên trên m t ph ng n m ngang. Tìm chuượ ứ ặ ẳ ằ
kỳ dao đ ng nh c a qu c u. Cho bi t mô men quán tính c a qu c u đ c làộ ỏ ủ ả ầ ế ủ ả ầ ặ
2
.
5
2rmI =
.
Câu 3 : (4 đi m)ể
M t gi t th y ngân l n n m gi a hai b n th y tinh n m ngang. D i tác d ngộ ọ ủ ớ ằ ữ ả ủ ằ ướ ụ
c a tr ng l c, gi t có d ng hình tròn b t có bán kính R= 3cm và b dày d = 0,5cm. ủ ọ ự ọ ạ ẹ ề
Tính kh i l ng c a m t v t n ng c n đ t lên b n trên đ kho ng cách gi aố ượ ủ ộ ậ ặ ầ ặ ả ể ả ữ
các b n gi m đi n = 9 l n. ả ả ầ Bi t góc b ế ở ờ
θ
= 1350.
Su t căng m t ngoài c a th y ngân là ấ ặ ủ ủ
σ
= 0,490 N/m,
2
= 1,41, g = 9,81
2
s
m
.
F
Câu 4: (4 đi m)ể
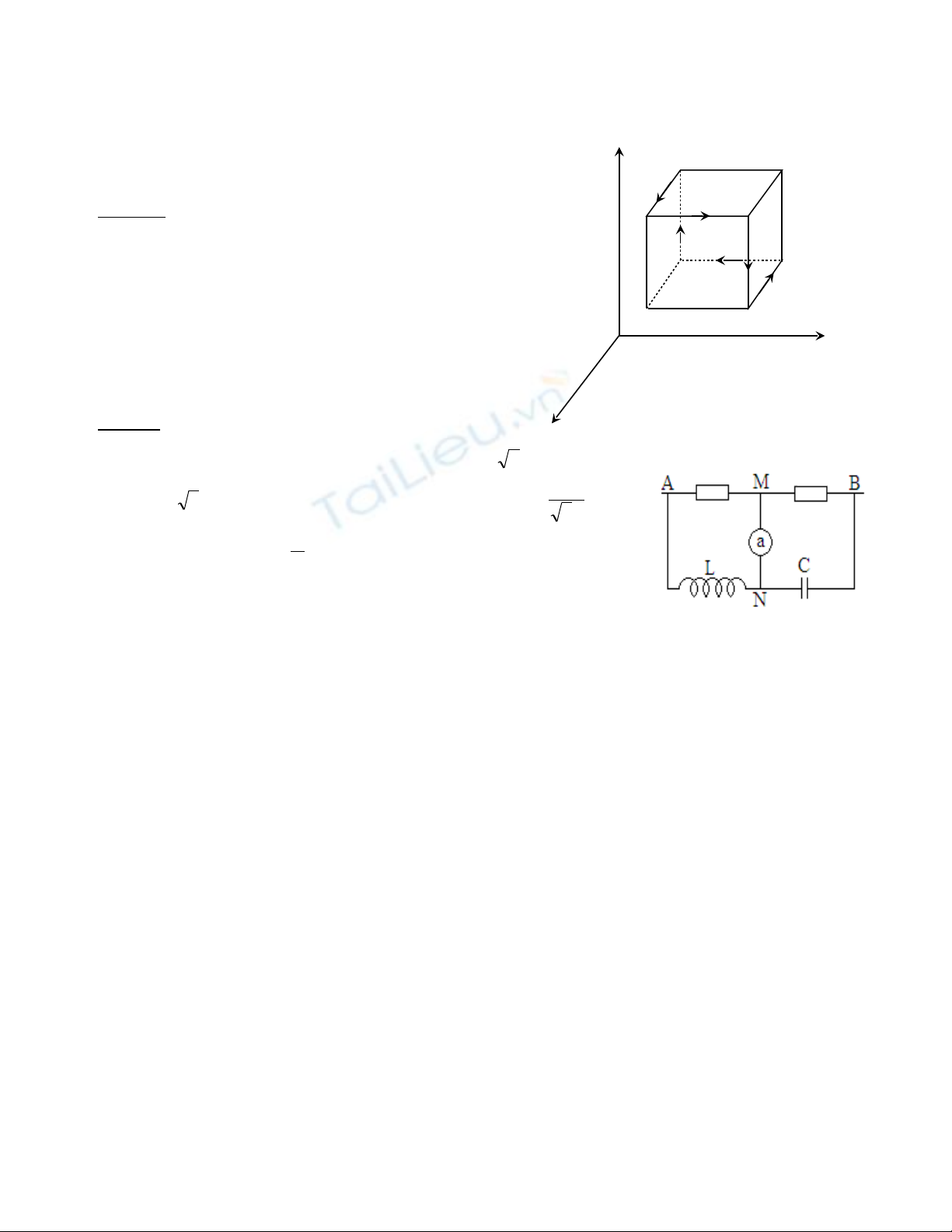
M t kh i l p ph ng c nh a cóộ ố ậ ươ ạ
dòng đi n c ng đ I ch y qua cácệ ườ ộ ạ
c nh c a nó theo m t đ ng nh hìnhạ ủ ộ ườ ư
v . Tìm c m ng t t i tâm c a kh iẽ ả ứ ừ ạ ủ ố
l p ph ng.ậ ươ
Câu 5: ( 4đi m)ể
Cho đo n m ch nh hình v : ạ ạ ư ẽ
tuAB
π
100sin2400=
(V)
R1 = 100
3
(Ω), R2 = 100(Ω).T có đi n dung C =ụ ệ
)(10
3
14F
−
π
;
cu n thu n c m L =ộ ầ ả
.Ampe k có đi n tr không đáng k .ế ệ ở ể
Xác đ nh s ch c a ampe k .ị ố ỉ ủ ế
O
A
BC
D
G
HE
F
z
y
x
R1R2
ĐÁP ÁN
Đáp án câu 1:
- Trước khi dây bị đứt: F – Fms = 0 ⇒ F = Fms (0,5đ)
- Ngay sau khi dây đứt: vật vẫn trượt đều với vận tốc v0; am = 0 (0,5đ)
Tấm ván chuyển động nhanh dần đều:
M
F
=
M
F
=
M
F
=a 1ms2ms
M
(0,5đ)
- Trường hợp vật không rời tấm ván:
+ Tấm ván đạt vận tốc v0 khi
F
Mv
=
a
v
=t 0
M
0
(0,5đ)
+ Sau đó vật cùng tấm ván chuyển động với gia tốc
m+M
F
=a
(0,5đ)
- Trường hợp vật rời khỏi tấm ván:
+ Vật chuyển động với gia tốc:
m
F
='am
, vận tốc ban đầu là v0
+ Tấm ván chuyển động thẳng đều, với vận tốc v’ < v0 khi vật rời khỏi tấm ván.
- Quãng đường vật đi được trên tấm ván (kể từ khi dây đứt)
F
Mv
tatvl M22
1
Δ
2
0
2
0=−=
-
Chiều dài tối thiểu của tấm ván:
F
Mv
llll 2
Δ
2
0
min +=+=
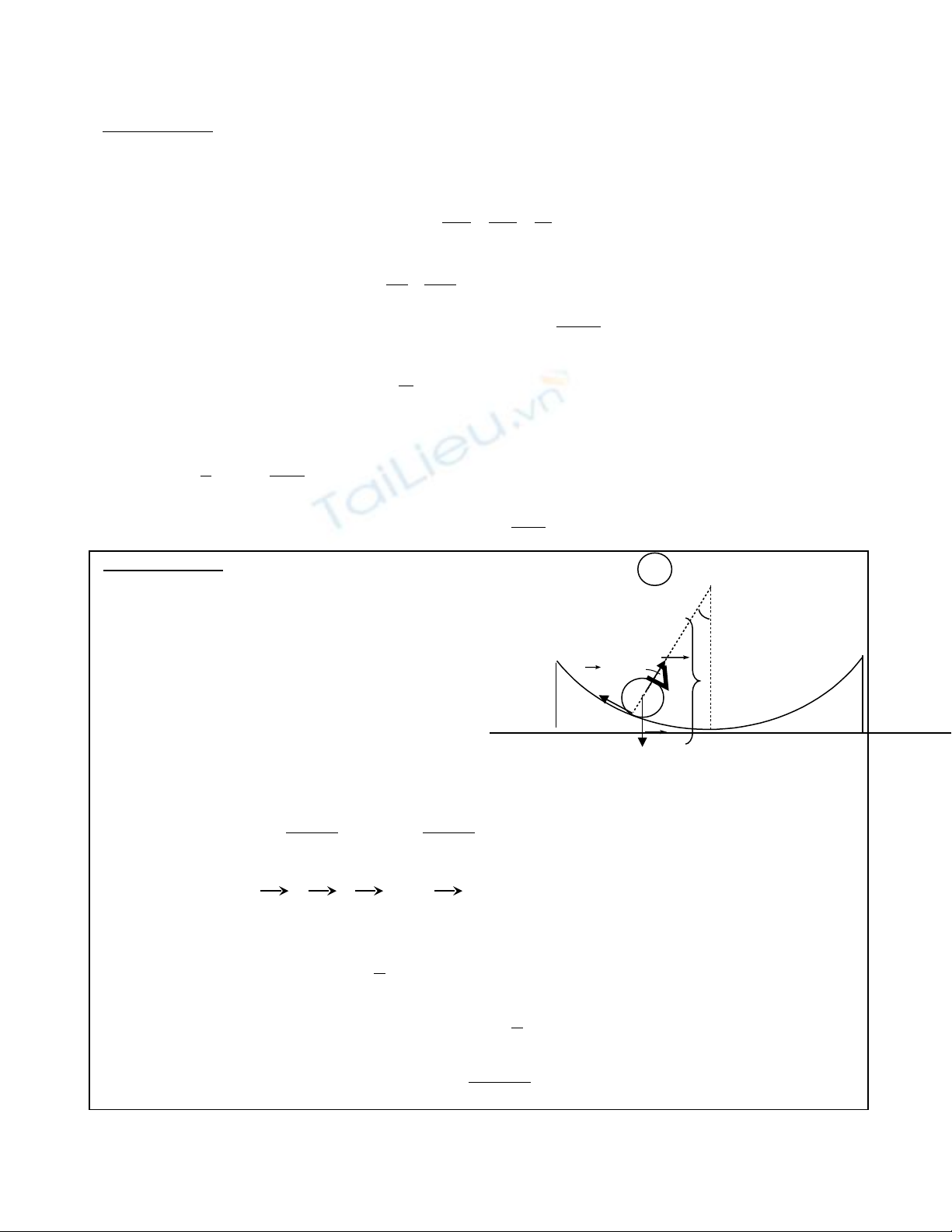
Đáp án câu 2 : XÐt thêi ®iÓm qu¶ cÇu lÖch so víi ph¬ng th¼ng ®øng mét gãc
ϕ
nhá, vµ
nã ®ang l¨n vÒ vÞ trÝ c©n b»ng (VTCB) (h×nh vÏ).
Gäi
1
ω
lµ vËn tèc gãc cña qu¶ cÇu quay quanh t©m O’ cña nã :
1
ω
=
'
β
2
ω
lµ vËn tèc gãc cña qu¶ cÇu quay quanh t©m O :
'
2
ω ϕ
=
Ta cã :
'
β
r =
'
ϕ
(R – r)
' '
( )
β ϕ
−
→ = R r
r
vµ
'' "
( )
β ϕ
−
=R r
r
(1)
XÐt chuyÓn ®éng quay cña qu¶ cÇu víi t©m quay tøc thêi K, ta cã ph¬ng tr×nh:
M(P)+M(N)+M(FMS)=Ik.β’’
Chän chiÒu híng vµo trong lµ chiÒu (+), ta cã:
- mgr sin
2 2 "
2
( )
5
ϕ β
= +mr mr
V×
ϕ
nhá nªn sin
ϕ
=
ϕ
do ®ã cã : - mgr.
2 "
7
5
ϕ β
=mr
(2)
Thay (1) vµo (2) ta cã ph¬ng tr×nh :
"
50
7( )
ϕ ϕ
+ =
−
g
R r
O
ϕ
R
o’
P
N
ms
F
K
+
§Æt
2
5
7( )
ω
=−
g
R r
→
" 2
0
ϕ ω ϕ
+ =
§©y lµ ph¬ng tr×nh dao ®éng ®iÒu hoµ cã chu kú T =
7( )
25
π
−R r
g
Đáp án câu 3:
mép c a gi t th y ngân, m t thoáng có d ng m t m t trònỞ ủ ọ ủ ặ ạ ộ ặ
xoay (hình chi c máng cong, xem hình). Ti t di n n m ngang làế ế ệ ằ
đ ng tròn bán kính R =3cm. Ti t di n th ng đ ng là cung trònườ ế ệ ẳ ứ
bán kính
r =
)cos(2
θπ
−
d
= -
θ
cos2
d
(0,25 đ)
R
Thay s r = ố
2
2
45cos2 0
dd =
(0,25 đ)
Áp su t t o nên b i m t thoáng c a gi t th y ngân là:ấ ạ ở ặ ủ ọ ủ
+= rR
p11
1
σ
=
+dR
21
σ
(0,25 đ)
L c c a áp su t ph tác d ng lên b n trên và cân b ng v i tr ng l c c a b n y là:ự ủ ấ ụ ụ ả ằ ớ ọ ự ủ ả ấ
22
11
21 R
dR
RpF
πσπ
+==
. (0,25 đ)
N u kho ng cách gi a hai b n gi m đi n = 9 l n thì :ế ả ữ ả ả ầ
d
→
d’=
9
d
n
d=
(0,25 đ)
R
→
R’ =
nR
=
RR 39 =
(0,5 đ)
L c c a áp su t ph tác d ng lên b n trên lúc này là:ự ủ ấ ụ ụ ả
22
22 '
'
2
'
1
'R
dR
RpF
πσπ
+==
V i d’ = ớ
n
d
; R’ =
nR
(0,5 đ)
Do đó
nR
d
n
nR
nRpF 22
22
21
πσπ
+==
(0,25 đ)
Tr ng l ng c a v t r n đ t lên b n trên b ng hi u s Fọ ượ ủ ậ ắ ặ ả ằ ệ ố 2 – F1
P = Mg = F2 – F1 (0,5 đ)
T đó suy ra : M = ừ
−+− d
nn
Rg
R2
)1()1(
12
2
πσ
. (0,5 đ)
Thay các giá tr b ng s :ị ằ ố
M =
+−
−
2
4
10.5,0
41,1
802
3
100
81,9
10.9.14,3.49,0
(0,5 đ)
M
≈
3,19 kg .
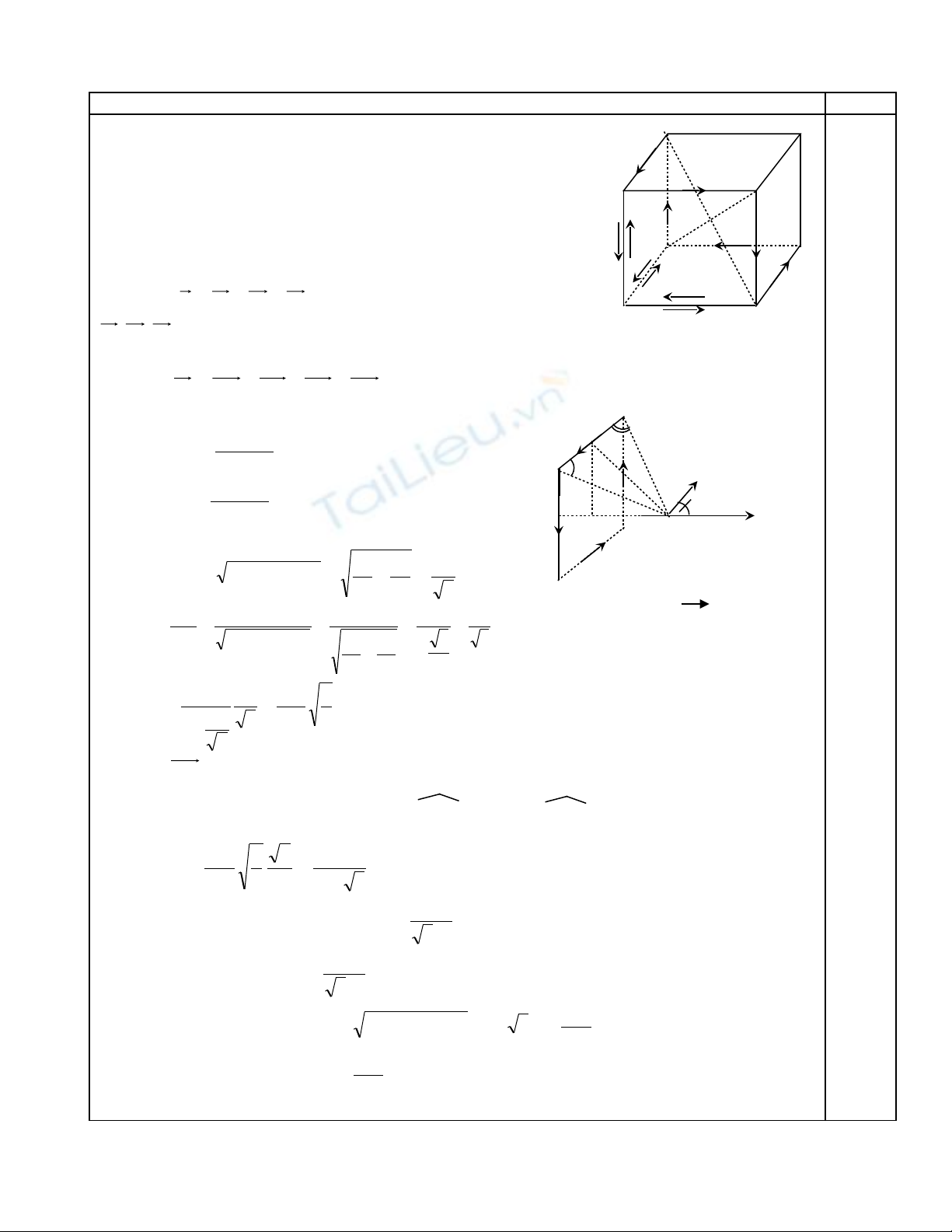
Đáp án câu 4
- Đ đ n gi n, ta có th xem trong m t c nh không cóể ơ ả ể ộ ạ
dòng đi n s t ng đ ng nh có 2 dòng đi n có c ng ệ ẽ ươ ươ ư ệ ườ
đ I ng c chi u đi qua c nh đó.ộ ượ ề ạ
- T hình v , ta th y s có 3 m t c a hình l p ph ng có ừ ẽ ấ ẽ ặ ủ ậ ươ
dòng đi n c ng đ I ch y qua c 4 c nh c a t ng m t, ệ ườ ộ ạ ả ạ ủ ừ ặ
đó là các m t AEFB, FEHG, ADHE.ặ
Do đó t tr ng do 3 m t gây ra tâm O là: ừ ườ ặ ở
321 BBBB ++=
321
,, BBB
l n l t là các vect c m ng t gây ra t i O b i các m t ầ ượ ơ ả ứ ừ ạ ở ặ
AEFB, FEHG, ADHE.
Xét
AEFBEF1 BBBBB AB +++=
T tr ng do c nh AB gây ra O:ừ ườ ạ ở
Ta có:
)cos(cos
.4 21
0
αα
π
µ
+= OM
I
BAB
α
π
µ
cos2
.4
0
OM
I
BAB =
(
ααα
== 21
)
V i: ớ
2
44
22
22
aaa
HMOHOM
=+=+=
3
1
2
3
2/
44
2/
cos
2222
==
+
=
+
==
a
a
aa
a
MBOM
MB
OB
MB
α
⇒
3
2
2
3
1
2
2
00
a
I
a
I
B
AB
π
µ
π
µ
==
Ta xét
AB
B
theo Oy thì:
MOHBMOHBBB ABABABABy sin90cos.cos 0=
−==
β
32
2
2
3
2
2
00
a
I
a
I
π
µ
π
µ
==
Do tính đ i x ng nên: ố ứ
a
I
BB ABy
π
µ
3
24 0
1==
T ng t : ươ ự
a
I
BB
π
µ
3
20
32 ==
,
C m ng t t i tâm O: ả ứ ừ ạ
a
I
BBBBBO
π
µ
0
1
2
3
2
2
2
123 ==++=
B0
a
I
π
µ
0
2=
0.25đ
0.25đ
0.25đ
0.25đ
0.25đ
0.25đ
0.25đ
0.25đ
0.25đ
0.25đ
0.5đ
0.5đ
0.5đ
A
BC
D
G
HE
F
21
35
6
4
O
A
B
E
F
H
M
O
1
α
2
α
β
y
BAB