1
www.VNMATH.com
Së gi¸o dôc - ®µo t¹o h¶I phßng ®Ò thi thö ®¹i häc
Trêng thpt trÇn nguyªn h·n M«n to¸n líp 12- n¨m häc 2011-2012
Thêi gian lµm bµi : 180phót
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH ( 07 điểm )
Câu I ( 2,0điểm) Cho hàm số
3 2 3
3 1
2 2
y x mx m
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m = 1
2. Tìm m để đồ thị hàm số có hai điểm cực đại , cực tiểu đối xứng qua đường thẳng y = x.
Câu II(2.0điểm)
1. Giải phương trình:
3 3 17
6 2 sin 2 8cos 2 2 cos( 4 )cos2
2
16
cos
x x x x
x
víi
5
( ; )
2 2
x
2. Giaûi heä phöông trình :
0222
0964
22
224
yxyx
yyxx
Câu III (1.0 điểm) Cho ph¬ng tr×nh
x x x 3
(7 3 5) a(7 3 5) 2
a,Gi¶i ph¬ng tr×nh khi a = 7
b, T×m a ®Ó ph¬ng tr×nh chØ cã mét nghiÖm
Câu IV(1.0 điểm) Cho khèi l¨ng trô ABC.A’B’C’ cã ®¸y ABC lµ tam gi¸c vu«ng c©n c¹nh huyÒn AB =
2
.
MÆt ph¼ng (A A’B) vu«ng gãc víi mÆt ph¼ng (ABC) , AA’ =
3
.Gãc
'
A AB
lµ gãc nhän vµ mÆt ph¼ng
(A’AC) t¹o víi mÆt ph¼ng (ABC) mét gãc 600 . TÝnh thÓ tÝch khèi l¨ng trô ABC.A’B’C’
Câu V(1.0 điểm) Cho
,
x y
, z lµ c¸c sè thùc d¬ng vµ tho¶ m·n ®iÒu kiÖn
1
x y z
. H·y t×m gi¸ trÞ nhá
nhÊt cña
1 1 1
(1 )(1 )(1 )
M
x y z
.
PHẦN RIÊNG CHO TỪNG CHƯƠNG TRÌNH ( 03 điểm )
(Thí sinh chỉ chọn một trong hai chương trình Chuẩn hoặc Nâng cao để làm bài.)
A/ Phần đề bài theo chương trình chuẩn
Câu VI.a: (2.0điểm)
1,Trong mặt phẳng với hệ toạ độ Oxy, hãy viết phương trình các cạnh của tam giác ABC biết trực tâm
(1;0)
H, chân đường cao hạ từ đỉnh B là
(0; 2)
K, trung điểm cạnh AB là
(3;1)
M.
2,T×m hÖ sè cña sè h¹ng chøa
6
x
trong khai triÓn
1
2
n
x
x
, biết rằng 2 1
1
4 6
n
n n
A C n
.
Câu VII.a: (1.0điểm) Giải phương trình:
2 3
8
2
4
log 1 2 log 4 log 4
x x x
B/ Phần đề bài theo chương trình nâng cao
Câu VI.b: (2 .0 điểm) 1, Trong mặt phẳng toạ độ Oxy cho hai đường thẳng (d1) : 4x - 3y - 12 = 0 và (d2): 4x +
3y - 12 = 0. Tìm toạ độ tâm và bán kính đường tròn nội tiếp tam giác có 3 cạnh nằm trên (d1), (d2), trục Oy.
2, Cho elip ( E ): 2 2
x y
1
16 9
và đường thẳng (d3): 3x + 4y = 0
a) Chứng minh rằng đường thẳng d3 cắt elip (E) tại hai điểm phân biệt A và B. Tìm toạ độ hai điểm đó
(với hành độ của điểm A nhỏ hơn hoành độ của của điểm B ).
b) Tìm điểm M (x ; y) thuộc (E) sao cho tam giác MAB có diện tích bằng 12.
2
www.VNMATH.com
Câu VII.b: (1.0 điểm) Giải hệ phương trình: 2
log ( 2 8) 6
8 2 .3 2.3
x x y x y
y x
-------------------HÕt -------------------
®¸p ¸n vµ biÓu ®iÓm Thi thö ®¹i häc lÇn 1
M«n to¸n líp 12- 2011-2012
Câu ý
Híng dÉn gi¶i chi tiÕt §iÓ
m
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH 7.00
Câu I 2
Khi m = 1 ta có 3 2
3 1
2 2
y x x
.
Tập xác định:
Sự biến thiên
-Giới hạn tại vô cực:
lim
xy


lim
xy


-Chiều biến thiên
Ta có 2
' 3 3
yxx
;
0
' 0
1
x
yx
3
www.VNMATH.com
Bảng biến thiên
x

0 1

y’ + 0 - 0 +
y
1
2

0

hàm số đồng biến trên khoảng
;0
 và
1;

,
hàm số nghịch biến trên khoảng
0;1
,
-Cực trị: Hàm số đạt cực đại tại x = 0,
1
(0)
2
CÐ
y y
Hàm số đạt cực tiểu tại x = 1,
1 0
CT
y y
3.
Đồ thị: Đồ thị cắt trục hoành tại điểm 1
;0
2
;
và cắt trục tung tại điểm
1
0;
2
. Đồ thị nhận điểm uốn
1 1
;
2 4
U
làm tâm đối xứng.
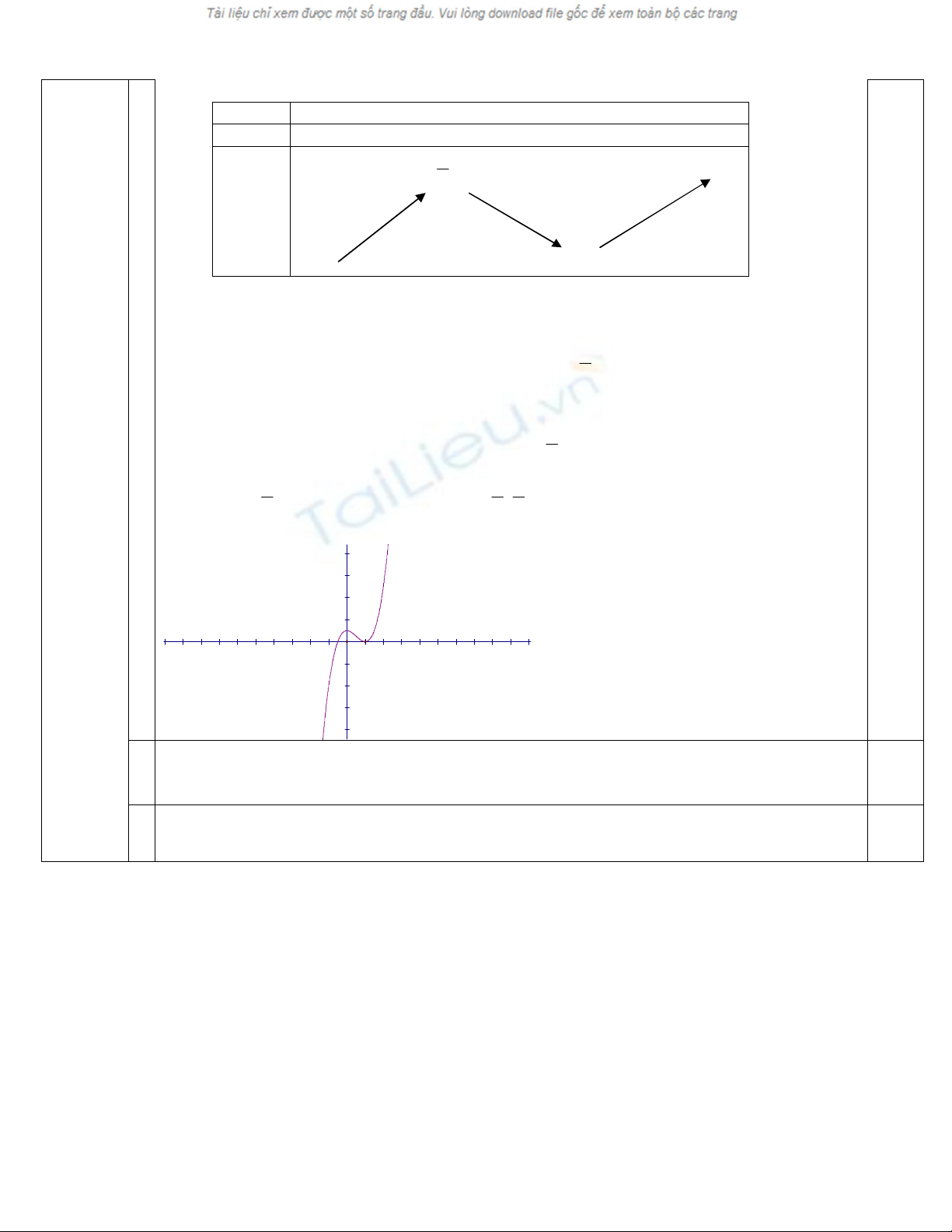
4
2
-2
-4
y
-10
-5
5
10
x
2
Tìm m để đồ thị hàm số có hai điểm cực đại , cực tiểu đối xứng qua đường thẳng y = x.
1
Ta có y’= 2
3 3
x mx
0
' 0 x
y
x m
0.25
4
www.VNMATH.com
Để đồ thị hàm số có cực đại, cực tiểu thì
' 0
y
có hai nghiệm phân biệt
0
m
. Khi đó
giả sử các điểm cực đại, cực tiểu là :
3
0;
2
m
A
và
; 0
B m
Ta có:
3
;
2
m
AB m
; trung điểm I của AB là:
3
;
2 4
m m
I
Theo yêu cầu bài toán để A và B đối xứng với nhau qua đường thẳng y = x thì
đường thẳng AB vuông góc với :
y x
và trung điểm I của AB thuộc đường thẳng
. 0
AB u
I

3
3
00
2
2
4 2
m
mm
m
m m
Đối chiếu điều kiện ta có
2
m
0.25
0.25
0.25
Câu II
2
1
1
Ta có:cos 0
2
x x k
0.25
Với đk pt(1)
3 2 2
8cos 6 2 sin 2 sin 2 cos 2 16cos
x x x x x
3
4cos 3 2 sin 2 8cos
x x x
2
(2cos 3 2 sin 4) 0
x x
2
2sin 3 2 sin 2 0
x x
2
4
32
4
x k
k
x k
Vậy phương trình đã cho có 2 nghiệm
5
( ; )
2 2
x
lµ
3 9
;
4 4
x x
0.5
2
1. 1
022)2(
4)3()2(
22
222
xyx
yx
0202)33)(42(
4)3()2(
22
222
xyx
yx
0202)33)(42(
4)3()2(
22
222
xyx
yx
§Æt
vy
ux
3
2
2 * Thay vµo ta cã hÖ pt
8)(4.
4
22
vuvu
vu
0.5
Gi¶I hÖ ta ®îc
0
2
v
uHoÆc
2
0
v
u
Thay vµo gi¶I ta cã
3
2
y
x ;
3
2
y
x;
5
2
y
x;
5
2
y
x
0.5
Câu III 1
5
www.VNMATH.com
7 3 5
( )
2
x
t
( t > 0) ta cã pt 2
8 0
t t a
(1)
Với a = 7 ta có 2
8 0
t t a
t 1
t 7
Ph¬ng tr×nh cã hai nghiÖm lµ 7 3 5
2
x 0
x log 7
0.5®
2, Sè nghiÖm cña pt (1) lµ sè nghiÖm t > 0 cña ph¬ng tr×nh 2
8
a t t
lµ sè ®iÓm chung
cña ®êng th¼ng y = a vµ ®å thÞ 2
8
y t t
víi t > 0
lËp b¶ng biÕn thiªn cña hµm sã 2
8
y t t
víi t > 0 kÕt luËn pt chØ cã mét nghiÖm khi
a = 16 hoÆc
0
a
0.5
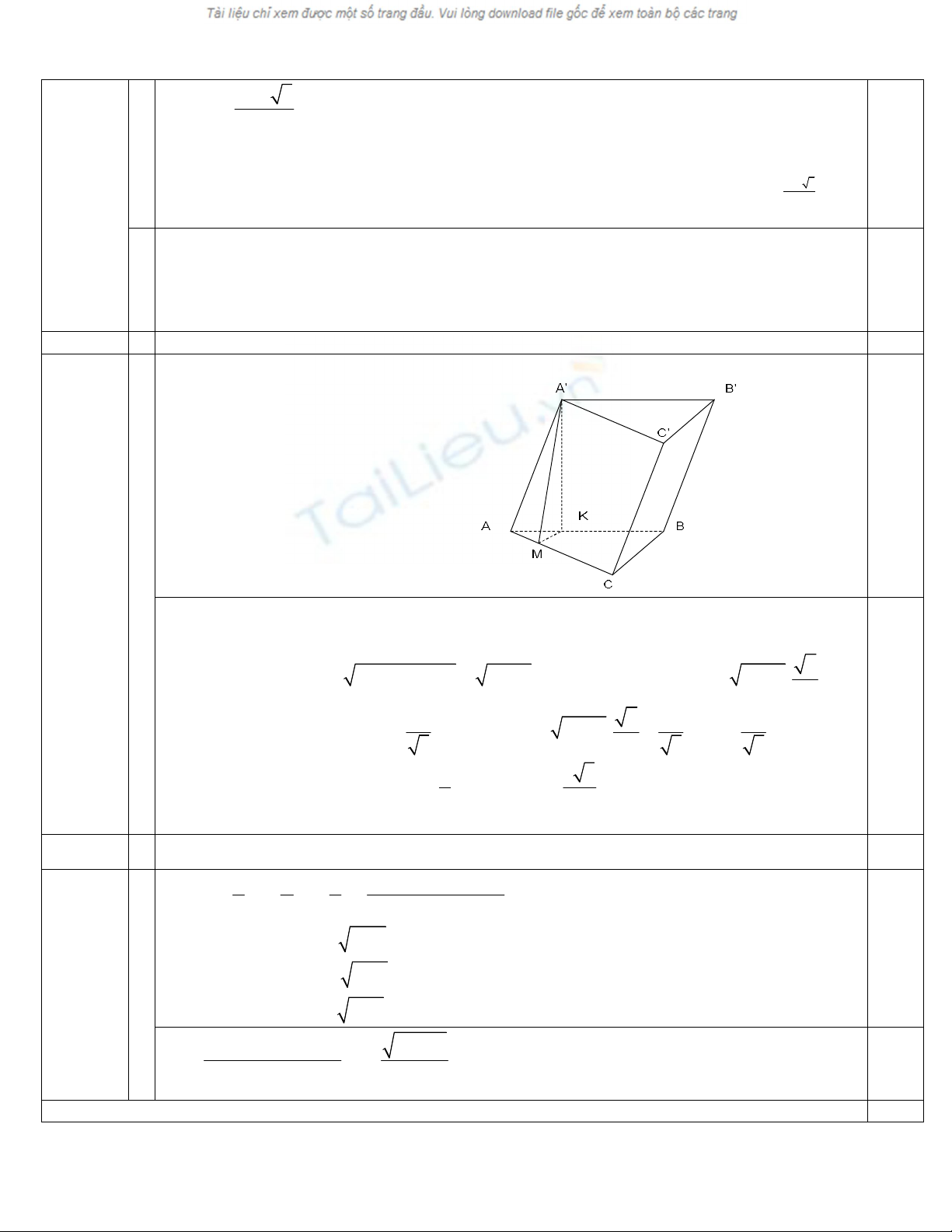
Câu IV
1
Gäi K., M lµ h×nh chiÕu cña A’ trªn AB vµ AC
cã :
( ' ) ( ) ' ( )
AA B ABC A K ABC
. Ta cã A’M
AC vµ KM
AC
0
' 60
A MK
,
'
A K x
. ta cã
2 2 2
' ' 3
AK A A A K x
, MK =
2
2
sin 3 .
2
AK KAM x
MÆt kh¸c
0
' cot60
3
x
MK A K vËy ta cã pt
2
2 3
3 . 2
3 5
x
x x
. ' ' '
1 3 5
. ' . . '
2 10
ABC A B C ABC
V S A K AC BC A K
0.5
0.5
Câu V 1
1 1 1 ( 1)( 1)( 1)
(1 )(1 )(1 ) x y z
Mx y x xyz
.
2
4
2
4
2
4
1 4
1 4
1 4
x x x y z x yz
y y x y z xy z
z z x y z xyz
0.25
0.25
0.25
4 4 4
4
( 1)( 1)( 1) 64
x y z
xyz
M
xyz xyz
. DÊu = x¶y ra khi x =y =z =1/3 0.25