ĐỀ THI THỬ ĐẠI HỌC, CAO ĐẲNG
Môn thi : TOÁN
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7 điểm )
Câu I ( 2,0 điểm ) Cho hàm số
1
1
x
y C
x
.
1. Khảo sát và vẽ đồ thị hàm số .
2. Xác định m để đường thẳng
2
y x m
cắt
C
tại hai điểm phân biệt A, B
sao cho tiếp tuyến của
C
tại A và B song song với nhau.
Câu II (2,0 điểm)
1. Giải phương trình : 2 2
3tan 4tan 4cot 3cot 2 0
x x x x
(1) .
2. Giải bất phương trình :
2
1 2 1
x x
(2) .
Câu III (1,0 điểm ) Tính diện tích hình phẳng giới hạn bởi đường :
2
: 4 3
P y x x
và hai tiếp tuyến của (P) tại hai điểm
0 ; 3 , 3; 0
A B
Câu IV (1,0 điểm )
Cho một hình chóp tứ giác đều có cạnh đáy là a, cạnh bên hợp với mặt đáy một
góc 600. Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp.Tính diện tích
mặt cầu.Tính thể tích khối cầu tương ứng .
Câu V ( 1,0 điểm ) Giải hệ phương trình , khi a > 1 :
2
2
1
3
1
3
a
x a y a z a
a
a
a x a y a z
a
II. PHẦN RIÊNG (3,0 điểm )Thí sinh chỉ được làm một trong hai phần ( phần
1 hoặc phần 2)
1). Theo chương trình Chuẩn :
Câu VI.a ( 2,0 điểm )Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có
phương trình :
2 2 2
: 2 4 6 0
S x y z x y z
1. Xét vị trí tương đối của mặt phẳng
: 0
x y z m
và mặt cầu (S) tùy
theo giá trị của m .
2. Tìm tọa độ giao điểm của (S) với đường thẳng () đi qua hai điểm
1;1;1
M
và
2 ; 1; 5
N
và viết phương trình các mặt phẳng tiếp xúc với mặt cầu (S) tại
các giao điểm đó .
Câu VII.a (1, 0 điểm ) Cho 8 quả cân có trọng lượng lần lượt là : 1 kg , 2 kg , 3
kg , 4 kg , 5 kg , 6 kg , 7 kg , 8 kg . Chọn ngẫu nhiên 3 quả cân trong số đó . Tính
xác suất để trọng lượng 3 quả cân được chọn không vượt quá 9 kg .

2). Theo chương trình nâng cao :
Câu VI.b ( 2,0 điểm ) 1. Trong mặt phẳng tọa độ Oxy, cho parabol
2
: 64
P y x
và đường thẳng
:4 3 46 0
x y
. Hãy viết phương trình đường tròn có tâm nằm trên đường
thẳng (∆) , tiếp xúc với parabol (P) và có bán kính nhỏ nhất .
2. Trong không gian với hệ tọa độ Oxyz cho ba điểm
2 ; 4 ; 1
A
,
1; 4 ; 0
B
0 ; 0 ; 3
C
.Xác định tâm và bán kính đường tròn (ABC) .
Câu VII. b (1, 0 điểm ) Có hai hộp chứa các viên bi chỉ khác về màu . Hộp thứ
nhất chứa 3 bi xanh , 2 bi vàng , 1 bi đỏ . Hộp 2 chứa 2 bi xanh , 1 bi vàng , 3 bi
đỏ . Lấy ngẫu nhiên từ mỗi hộp một viên bi . Tính xác suất để lấy được 2 bi xanh .
Lôøi giaûi
Câu I.
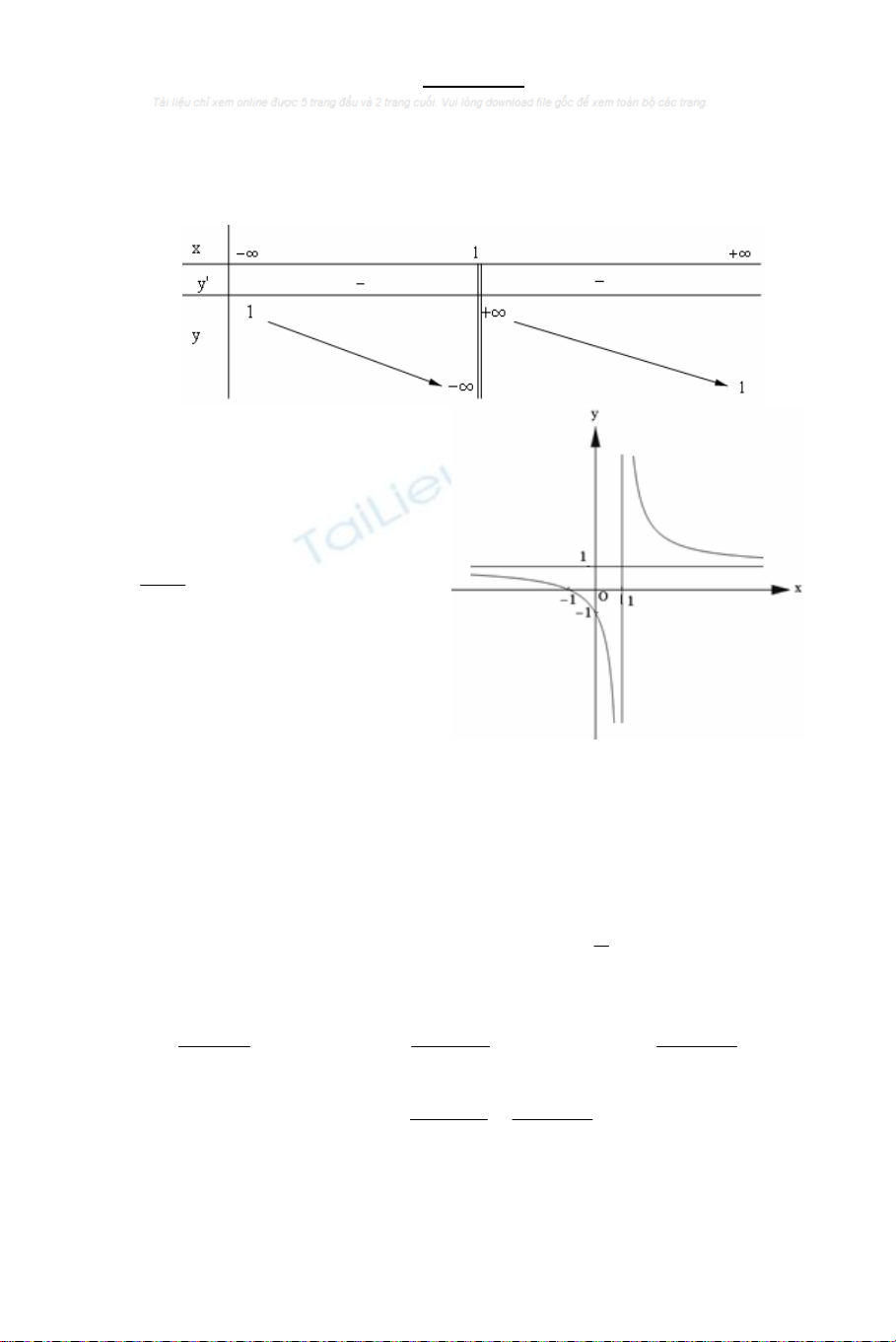
1. Phần khảo sát chi tiết bạn đọc tự làm , dưới đây là bảng biến thiên và đồ thị
(C) của hàm số .
+ Bảng biến thiên :
+ Đồ thị (C) :
2. Phương trình hoành độ giao điểm của
: 2
d y x m
và
C
:
12
1
x
x m
x
2
2 3 1 0 1
1
x m x m
x
Ta có:
2 2
3 8 1 1 16 0,
1 2 0,
m m m m
g m
phương trình (1) luôn luôn có hai nghiệm phân biệt khác 1.
Vậy
d
luôn luôn cắt
C
tại hai điểm phân biệt A và B .
Gọi
1 2
,
x x
1 2
x x
lần lượt hoành độ của A và B thì
1 2
,
x x
là nghiệm của
phương trình (1). Theo định lí Vi-et, ta có:
1 2 13
2
x x m
Tiếp tuyến
1 2
,
tại A, B có hệ số góc lần lượt là :
Vì
2
2
'
1
yx
1 1
2
1
2
'
1
k y x x
,
2 2
2
2
2
'
1
k y x x
1 2 1 2
/ /
k k
2 2
1 2
2 2
1 1
x x
2 2
1 2
1 1
x x

1 2
1 2
1 1
1 1
x x
x x
1 2
1 2 2
x x
x x
loaïi
1
3 2
2
m
1
m
.
Vậy, giá trị cần tìm là:
1
m
.
Câu II (2,0 điểm)
1. Giải phương trình
Điều kiện : sin 0 sin2 0 ,
cos 0 2
xx x k k
x
¢
2 2
1 3 tan cot 4 tan cot 2 0
x x x x
Đặt 2
tan cot , 2
sin 2
t x x t
x
2 2 2
tan cot 2
t x x
2 2 2
tan cot 2
x x t
Ta có :
2
3 2 4 2 0
t t
2
3 4 4 0
t t
2
2
3
t
t
loaïi
2
2
sin2
x
sin 2 1
x
2 2 ,
2
x l l
¢
,
4
x l l
¢
So với điều kiện, ta có nghiệm của phương trình : ,
4
x l l
¢
.
2. (1)
2
2
2
2 1 0
1 0
2 1 1
x
x
x x
2
1 1
1
2 3 0
x x
x
x x
1
1
1 3
x
x
x
1
1 3
x
x
Vậy nghiệm của bất phương trình :
1 1 3
x x
.
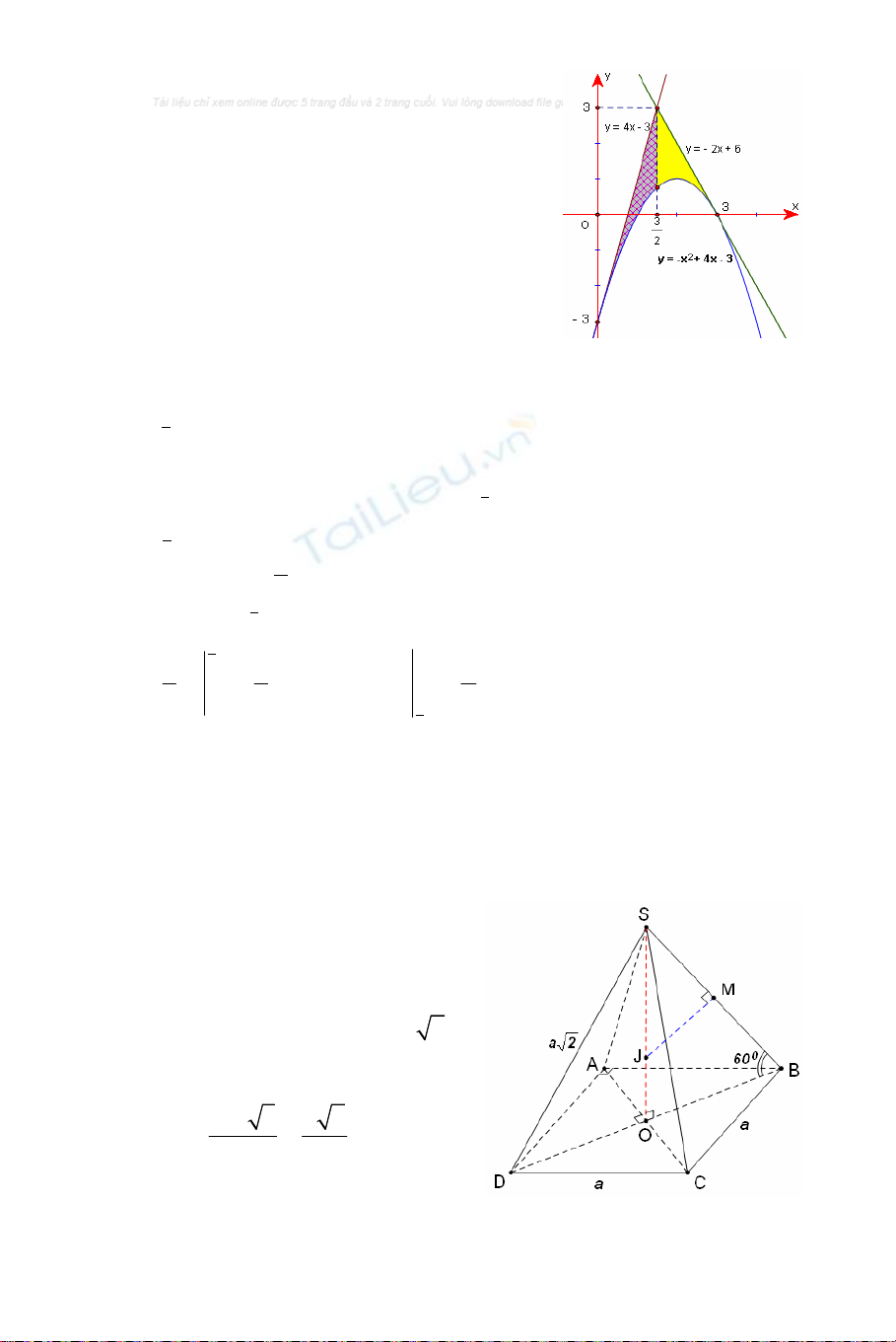
Câu III .
' 0 4
' 2 4
' 3 2
y
y x x y
+ Phương trình tiếp tuyến 1 của (P) tại A có dạng:
1
1
: 3 ' 0 0
: 4 3
y y x
y x
+ Phương trình tiếp tuyến 2 của (P) tại B có dạng:
2
2
: ' 3 3
: 2 6
y y x
y x
Dựa vào đồ thị ta có diện tích hình phẳng cần tìm là:
33
22 2
3
02
4 3 4 3 2 6 4 3
S x x x dx x x x dx
33
22 3 2
0 3
2
1
. 3 9
3
x dx x x x dx
3
3
2
3 3 2
3
0
2
1 1 3 9
3 3
x x x x
9
4
(đvdt) .
Câu IV.
* Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp.Gọi O là tâm của đáy
, suy ra
SO ABCD
nên SO là trục của đường tròn ngoại tiếp đáy ABCD của
hình chóp. Trong
SOB
kẻ đường trung trực Mx của cạnh SB .
Gọi
Mx SO J JA JB JC JD JS
nên J là tâm của mặt cầu ngoại tiếp hình chóp S.ABCD.
Ta có
ABCD
OB hch SB
·
·
0
, 60
SB ABCD SBO
nên
SBD
đều , có cạnh
2
BD a
.
Bán kính của mặt cầu ngoại tiếp chính là
bán kính đường tròn ngoại tiếp
SBD
Do đó
. 3 6
3 3
BD a
R .






















![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



