Câu 1:
Cho hàm số y =
2 3
2
x
x
có đồ thị là (C)
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số trên.
2) Tìm trên (C) những điểm M sao cho tiếp tuyến tại M của (C) cắt 2 tiệm cận của (C)
tại A, B sao cho AB ngắn nhất.
Câu 2:
1) Giải phương trình:
2 2sin( ).cos 1
12
x x
2) Giải hệ phương trình: 3 3 3
2 2
8 27 18 (1)
4 6 (2)
x y y
x y x y
Câu 3:
1) Tính tích phân I =
22
6
1
sin sin
2
x x dx
2) Tìm các giá trị của tham số thực m sao cho phương trình sau có nghiệm thực:
(m - 3)
x
+ ( 2- m)x + 3 - m = 0. (1)
Câu 4: Cho ba số thực dương a, b, c thỏa mãn abc = 1. Chứng minh rằng:
3 3 3
1
8 1 8 1 8 1
a b c
c a b

Câu 5:
Cho hình chóp S. ABC có góc ((SBC), (ACB)) =600, ABC và SBC là các tam
giác đều cạnh a. Tính theo a khoảng cách từ B đến mặt phẳng (SAC).
PHẦN RIÊNG
1. Theo chương trình chuẩn:
Câu 6a: Cho ABC có B(1;2), phân giác trong góc A có phương trình ( ) 2x +y –1
=0; khoảng cách từ C đến ( ) bằng 2 lần khoảng cách từ B đến (). Tìm A, C biết C
thuộc trục tung.
Câu 7a: Trong không gian Oxyz cho mp(P): x –2y +z -2 =0 và hai đường thẳng :
(d1)
3
2
1
1 1 2
y
z
x
; (d2)
1 2
2 ( )
1
x t
y t t
z t
¡
. Viết phương trình tham số của đường
thẳng nằm trong mp(P) và cắt cả 2 đường thẳng (d1) , (d2)
2. Theo chương trình nâng cao:
Câu 6b: Cho ABC có diện tích bằng 3/2; A(2;–3), B(3;–2), trọng tâm G (d) 3x –y –
8 =0. tìm bán kinh đường tròn nội tiếp ABC.
Câu 7b: Trong không gian Oxyz cho đường thẳng (d) là giao tuyến của 2 mặt phẳng:
(P): 2x–2y–z +1 =0, (Q): x+2y –2z –4 =0 và mặt cầu (S): x2 +y2 +z2 +4x –6y +m =0. Tìm
tất cả các giá trị của m để (S) cắt (d) tại 2 điểm MN sao cho MN= 8.
...................................................
Đáp án ĐỀ THI THỬ ĐẠI HỌC, CAO ĐẲNG
Phần chung:
Câu 1: Cho hàm số y =
2 3
2
x
x
có đồ thị là (C)
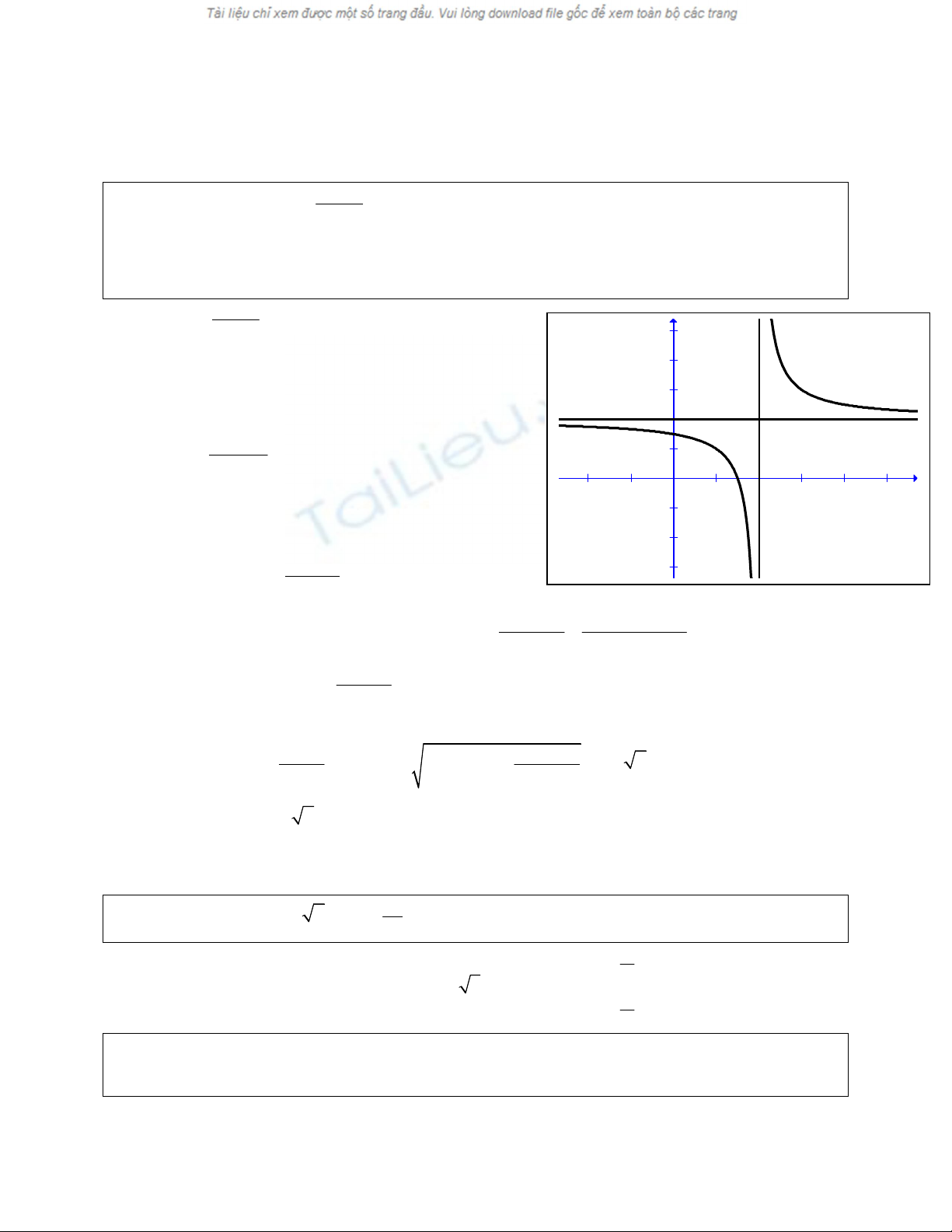
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số trên.
2) Tìm trên (C) những điểm M sao cho tiếp tuyến tại M của (C) cắt 2 tiệm cận của (C)
tại A, b sao cho AB ngắn nhất.
Giải: 1) y=
2 3
2
x
x
(C)
D= R\ {2}
lim 2 : 2
x
y TCN y

2 2
lim ;lim
x x
y y
 
TCĐ x = 2
y’ = 2
1
0; 2
( 2) x
x
BBT
2) Gọi M(xo; 0
0
2 3
2
x
x
) (C) .
Phương trình tiếp tuyến tại M: () y = 2
0 0
2 2
0 0
2 6 6
( 2) ( 2)
x x
x
x x
( ) TCĐ = A (2; 0
0
2 2
2
x
x
)
( ) TCN = B (2x0 –2; 2)
00
2
(2 4; )
2
AB x x
uuur
AB = 2
02
0
4
4( 2) 2 2
( 2)
cauchy
xx
AB min =
2 2
0
3 (3;3)
1 (1;1)
o
x M
x M
Câu 2:
1) Giải phương trình:
2 2sin( ).cos 1
12
x x
Giải: phương trình 2(cosx–sinx)(sinx–
3
cosx)=0 3
( )
4
x k k
x k
¢
2) Giải hệ phương trình: 3 3 3
2 2
8 27 18 (1)
4 6 (2)
x y y
x y x y
-2 -1 1 2 3 4 5
-3
-2
-1
1
2
3
4
5
x
y
Giải: (1) y 0
Hệ
3
33
3
2
2
27 3
8 18
(2 ) 18
4 6 3 3
1
2 . 2 3
xx
yy
x x x x
y y y y
Đặt a = 2x; b =
3
y
. Ta có hệ: 3 3
3
18
1
( ) 3
a b
a b
ab
ab a b
Hệ đã cho có 2 nghiệm 3 5 6 3 5 6
; , ;
4 4
3 5 3 5
Câu 3:
1) Tính tích phân I =
22
6
1
sin sin
2
x x dx
Giải: I =
22
6
3
cos (cos )
2
x d x
.
§Æt 3
cos cos
2
x u
I
2
4
2
sin
2
3
udu =
3
2
16
2) Tìm các giá trị của tham số thực m sao cho phương trình sau có nghiệm thực:
(m - 3)
x
+ ( 2- m)x + 3 - m = 0. (1)
Giải: Đk x 0. đặt t =
x
; t 0
(1) trở thành (m–3)t+(2-m)t2 +3-m = 0 2
2
2 3 3
1
t t
m
t t
(2)
Xét hàm số f(t) = 2
2
2 3 3
1
t t
t t
(t 0)
Lập bảng biến thiên
(1) có nghiệm (2) có nghiệm t 0
5
3
3
m
Câu 4: Cho ba số thực dương a, b, c thỏa mãn abc = 1. Chứng minh rằng:
3 3 3
1
8 1 8 1 8 1
a b c
c a b

Giải: