SỞ GIÁO DỤC – ĐÀO TẠO THÁI BÌNH ĐỀ THI THỬ TUYỂN SINH ĐẠI HỌC
TRƯỜNG THPT LÊ QUÝ ĐÔN MÔN THI: TOÁN KHỐI D LẦN 2
Đề chính thức
Thời gian làm bài :180 phút (không kể thời gian phát đề)
I/PHẦN CHUNG CHO TẤT CẢ THÍ SINH
Câu I: (2điểm) Cho hàm số
2
x m
y
x
(Cm)
1/Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m=1
2/Tìm các giá trị thực của tham số m để đường thẳng d; 2x+2y -1=0 cắt đồ thị (Cm) tại hai điểm
phân biệt A,B sao cho tam giác
OAB
có diện tích bằng 1 đơn vị diện tích (O là gốc toạ độ)
Câu II: (2điểm) 1/Giải phương trình:
2cos(2x ) 4sinx.sin3x-1 0
2/Giải phương trình : 2
4 2 2
2.log log .log ( 2 1 1)
x x x
Câu III: (1điểm)Tính tích phân :
13
2
x 3x 2
dx
x 2
Câu IV: (1điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có góc
·
0
60
ABC ,hai mặt phẳng
(SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD),góc giữa hai mặt phẳng (SAB) và (ABCD)
bằng 300 .Tính thể tích khối chóp S.ABCD và khoảng cách giữa hai đường thẳng SA,CD theo a
Câu V: (1điểm) Cho x,y là các số thực thay đổi và thoả mãn điều kiện .
2 2
1
x y xy
. Tìm giá trị lớn nhất , nhỏ nhất của biểu thức
2 2
P x y xy
II/PHẦN RIÊNG: Thí sinh chỉ được làm 1 trong 2 phần(Phần A hoặc phần B)
A/Theo chương trình chuẩn
Câu VIa: (1điểm)
Trong mặt phẳng với hệ toạ độ Oxy cho điểm M(6;2) và đường tròn (C): 2 2
(x 1) (y 2) 5
.Viết
phương trình đường thẳng (d) đi qua M và cắt đường tròn (C)tại hai điểm A,B sao cho
AB 10
Câu VIIa: (1điểm)
Trong không gian Oxyz ,cho đường thẳng (d) :
1 1
2 4 1
x y z
và hai điểm phân biệt A(4;-1;1)
B(2;5;0) .Tìm điểm M trên đường thẳng (d) sao cho tam giác
MAB
vuông tại M
Câu VIIIa: (1điểm)
Trong mặt phẳng toạ độ .Tìm tập hợp các điểm biểu diễn số phức z thoả mãn
2 3
z i z i
.Trong các số phức thoả mãn điều kiện trên ,tìm số phức có mô đun nhỏ nhất
B/Theo chương trình nâng cao
Câu VIb: (2điểm)
Trong mặt phẳng với hệ toạ độ Oxy ,cho A(-1;2) và đường thẳng
(d): x 2y 3 0
.Tìm trên
đường thẳng (d) hai điểm B,C sao cho tam giác
ABC
vuông tại C và AC=3BC
Câu VIIb: (1điểm)
Trong không gian Oxyz ,cho mặt phẳng (P) :
x 2 3 0
y z
và
1 2
x 1 y 1 z 1 x 1 y 2 z 1
d : ;d :
2 1 1 1 1 2
.Viết phương trình chính tắc của đường thẳng
biết
chứa trong mặt phẳng (P) và cắt cả hai đường thẳng
1
d
,
2
d
Câu VIIIb:
Tìm số phức z thoả mãn
( 1)( 2 )
z z i
là số thực và
z
nhỏ nhất
_________HẾT_________
(Cán bộ coi thi không giải thích gì thêm)
Họ và tên thí sinh:...............................................................Số báo danh.........................
SỞ GIÁO DỤC-ĐÀO TẠO THÁI BÌNH
TRƯỜNG THPT LÊ QUÝ ĐÔN HƯỚNG DẪN CHẤM THI THỬ ĐẠI HỌC
MÔN TOÁN KHỐI D
HỌC KỲ II NĂM HỌC 2011-2012
Câu
NỘI DUNG Điểm
I 1. Khi m=1 .khảo sát và vẽ đồ thị hàm số
1
2
x
y
x
1
a)TXĐ:
D \ 2
¡
b)Sự biến thiên
-Chiều biến thiên 2
3
' 0 2
( 2)
y x
x
………………………………………………………………………………………...
Hàm số nghịch biến trên các khoảng
( ; 2)

và
( 2; )

-Cực trị : Hàm số không có cực trị
-Giới hạn :
lim 1 ; lim 1
x x 
.Đường thẳng y = -1 là tiệm cân ngang của đồ thị
hàm số
2 2
lim ; lim
x x
y

 
.Đường thẳng x = -2 là tiệm cân đứng của đồ thị hàm số
………………………………………………………………………………………...
Bảng biến thiên
………………………………………………………………………………………...
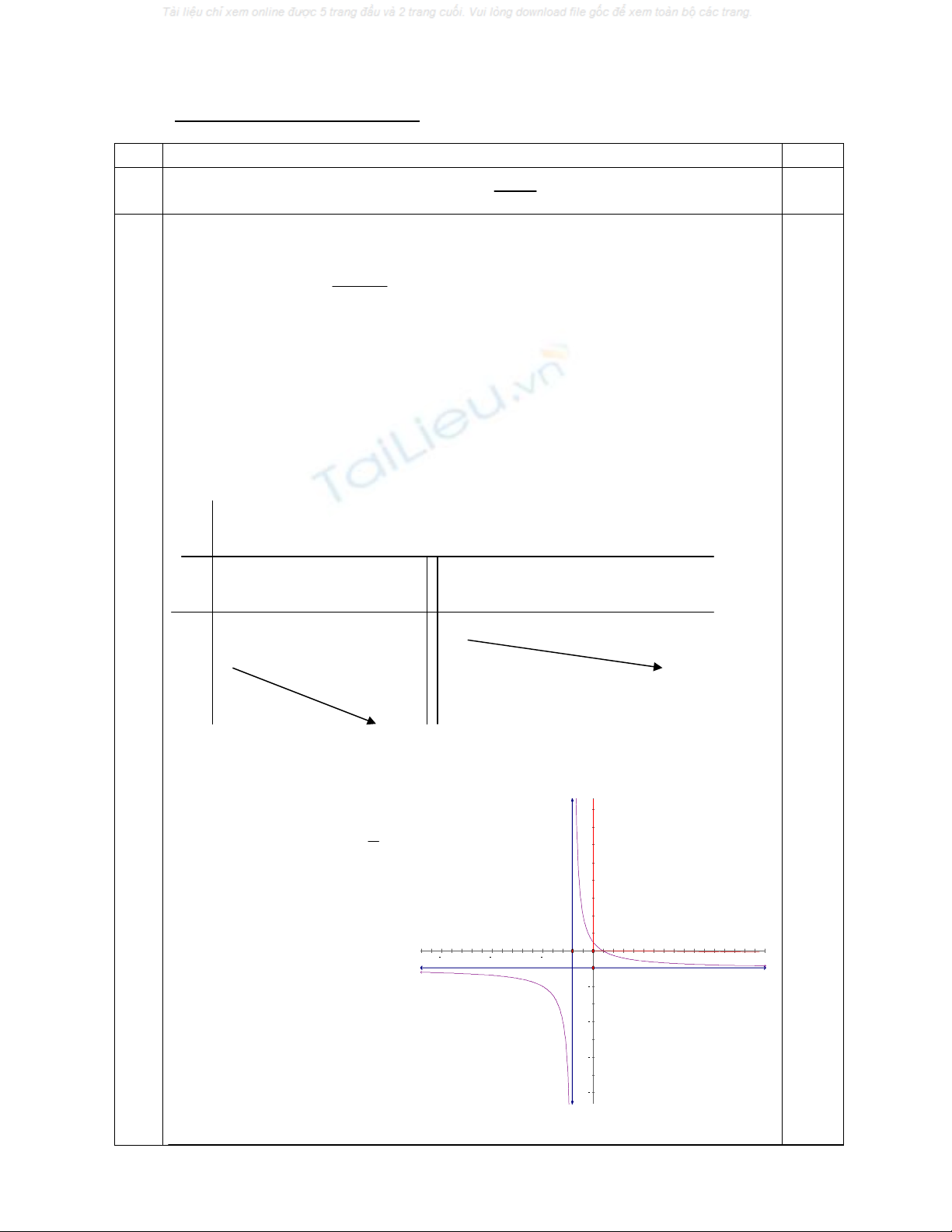
Đồ thị
*Giao với trục Ox tại A(1;0)
*Giao với trục Oy tại
1
B(0; )
2
* Đồ thị nhận I(-2;-1) giao của
hai tiệm cận làm tâm đối xứng
8
6
4
2
2
4
6
8
15 10 5 5 10 15
O
-2
-1
2:Tìm m để đường thẳng d: 2x+2y-1=0 cắt đồ thị (C) tại hai điểm phân biệt A,B, sao
cho tam giác ABC có diện tích bằng 1
0.25
0.25
0.25
0.25
1
y'
-
2
x
y


- -
1


1
TXĐ:
D \ 2
¡ Đường thẳng d:y=-x +
1
2
.
Phương trình hoành độ giao điểm của đường thẳng (d) và(Cm) là
1
2 2
x m x
x
2
2 2 2 0
x x m
(1) .Đường thẳng (d) cắt (Cm) tại 2 điểm
A,B
(1) có hai nghiệm phân biệt
2
x
2
17
1 8(2 2) 0 17 16 0
16
2
2.( 2) ( 2) 2 2 0
2
mmm
m
mm
với
17
16
2
m
m
đường thẳng (d) y=-x +
1
2
cắt (Cm) tại 2 điểm phân biệt
1 1 2 2
1 1
A(x ; x ),B(x ; x )
2 2
trong đó x1;x2 là hai nghiệm phân biệt của phương
trình 2
2 2 2 0
x x m
theo viet ta có 1 2
1 2
1
x x
2
x .x m 1
2 2 2
2 1 1 2 2 1 1 2
2(17 16m)
AB (x x ) (x x ) 2 (x x ) 4x x
2
1
d O,d
; OAB
2(17 16m)
1 1 1 47
S AB.d(O,d) . . 1 m
2 2 2 16
2 2
(t/m)
Vậy với
47
m
16
thì đường thẳng d: 2x+2y-1=0 cắt đồ thị (C) tại hai điểm phân biệt
A,B, sao cho tam giác ABC có diện tích bằng 1
0.25
0.25
0.25
0.25
II
2.0đ
1: Giải phương trình :
2cos(2x ) 4sinxsin3x 1 0
(1) 1
phương trình (1)
2
2(cos2xcos sin 2xsin ) 4sin xsin3x 1 0
3 3
cos2x 3sin2x+4sin xsin3x 1 0
1 2sin x-2 3sin x cosx 4sin xsin3x 1 0
sinx(2sin3x-sin x- 3 cos x) 0
sinx 0
sinx 3cosx 2sin3x
*sinx 0 (k z)
x k
1 3
*sinx 3cosx 2sin3x sinx cosx sin3x
2 2
3x x k2 x k
3 6
sin(x ) sin3x (k z)
33x x k2 x k
3 6 2
vậy phương trình đã cho có nghiệm
x k
;
x k
6 2
(k z)
0.25
0.25
0.25
0.25
2.Giải phương trình 2
4 2 2
2log log .log ( 1 1)
x x x
(1)
Điều kiện x>0 (1) 2
2 2 2
1
log log .log ( 1 1) 0
2
x x x
2 2 2
1
log ( log log ( 1 1)) 0
2
x x x
2
2 2
log x 0 x 1 x 1
1
x 0 (ktm)
log x log ( x 1 1) 0 x 1 1 x
2
Kết hợp điều kiện phương trình đã cho có nghiệm x =1
1
0.25
0.25
0.25
0.25
III Tính tích phân 13
2
x 3x 2
I dx
x-2
1
Ta có
1 1 1
2
3
2 2 2
1
2
1 2
( 1) ( 2)
3 2
dx = dx= dx
x-2 x-2 x-2
(1 ) 2
= dx
x-2
x x
x x
x x
x x
Đặt 2 2
t x 2 t x 2 x t 2
dx 2tdt
: Đổi cận khi x = -2 thì t = 0 ; khi x = -1 thì t = 1
1 1 1
2 4 2 2
2 2 2
0 0 0
(1 t 2)t t 3t 4
I .2tdt =2 dt 2 ( t 1 )dt
t -2-2 t -4 t -4
Xét
1
13
2
00
t 8
J=2 ( t 1)dt 2( t)
3 3
Xét
1
1 1
2
0 0 0
4 1 1 2 t
K=-2 dt 2 ( )dt 2ln 2ln3
t -4 2 t 2 t 2 t
Vậy I=
2ln3
-
8
3
0.25
0.25
0.25
0.25
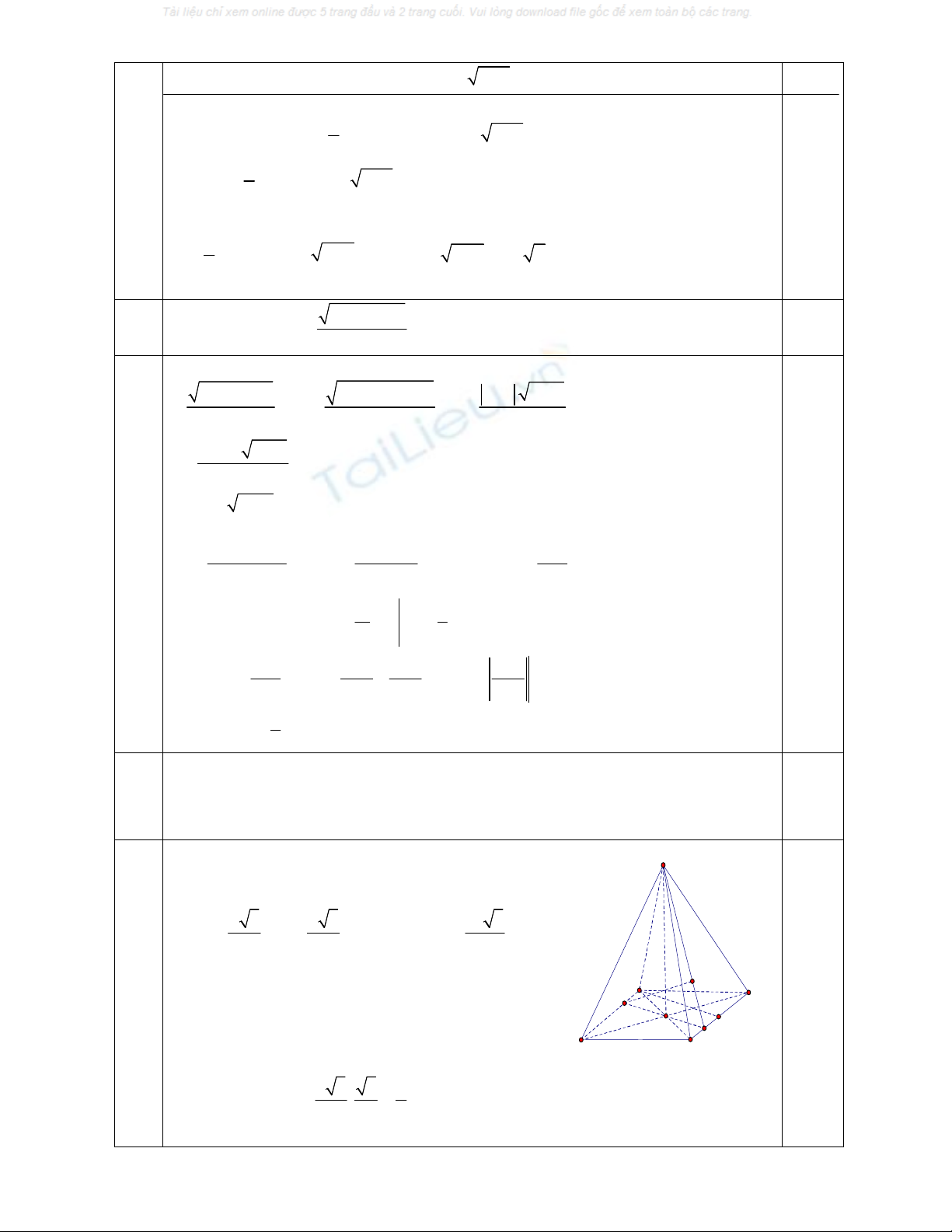
IV Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có góc
·
0
60
ABC ,hai
mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD),góc giữa hai mặt
phẳng (SAB) và (ABCD) bằng 300 .Tính thể tích khối chóp S.ABCD và khoảng cách
giữa hai đường thẳng SA,CD theo a
1
Gọi
O AC BD
,M là trung điểm của AB và I là
trung điểm của AM theo giả thiết ta có tam giác
ABC đều cạnh a nên
CM AB,OI AB
và
2
3 3 3
, ,S 2
2 4 2
ABCD ABC
a a a
CM OI S
…………………………………………………
Vì(SAC)và (SBD) cùng vuông góc với (ABCD)
nên
SO (ABCD)
do
AB OI AB SI
.Suy ra
·
·
·
0
(SAB,(ABCD) (OI,SI) SIO 30
Xét tam giác vuông
SOI ta được
:0
a 3 3 a
SO OI.tan30 .
4 3 4
Thể tích khối chóp S.ABCD là
O
D
A
C
B
S
J
I
M
H
0.25
0.25
2 3
1 1 3 3
.
3 3 2 4 24
ABCD
a a a
V SO S
Gọi
J OI CD
và H là hình chiếu vuông góc của J trên SI ta có
a 3
IJ 2OI
2
và
JH (SAB)
Do CD AB (SAB)
CD (SAB)
CD (SAB)
PP
d(SA,CD) d CD,(SAB) d (J,(SAB) JH
Xét tam giác vuông
IJH
ta được 0
a 3 1 a 3
JH IJ.sin30 .
2 2 4
Vậy
a 3
d(SA,CD)
4
0.25
0.25
V Cho x,y là các số thực thay đổi và thoả mãn điều kiện .
2 2
1
x y xy
. Tìm giá trị lớn nhất , nhỏ nhất của biểu thức
2 2
P x y xy
1
Từ 2 2 2 2 2 2
P xy(x y) P (xy) (x y 2xy) x y (1 3xy)
Đặt t=xy
2 2 2
1
x y xy 1 1 3xy (x y) 0 t
3
2 2 2
x y xy 1 (x y) 1 xy 0 t 1
2 2
2
1
P f (t) t (1 3t) ,t 1;3
t 0
f '(t) 2t 9t f '(t) 0
2
t
9
Có 2
1 2 4
( 1) 4; (0) ( ) 0 ,f( ) 4 2 2
3 9 243
f f f P P
P 2 x 1,y 1 maxP 2
P 2 x 1, y 1 min P 2
0.25
0.25
0.25
0.25
TỰ CHỌN
A:THEO CHƯƠNG TRÌNH CHUẨN
VIa
8
6
4
2
2
4
6
8
O
15 10 5 5 10 15
B
I
A
H
M
Đường tròn (C)Có tâm I (1;2) và bán kính R=
5
.Gọi H là hình chiếu vuông góc
của I trên AB theo tính chất đường kính dây cung H là trung điểm của AB ta có
2
2 2 2 2
AB 10 5 10
IH IA AH R 5 IH
4 4 2 2
Gọi đường thẳng (d) đi qua M và có véc tơ pháp tuyến 2 2
n (a;b) (a b 0)
r
Ptđt(d):
a(x 6) b(y 2) 0 ax by 6a 2b 0
0.25
0.25