Së gi¸o dôc v ®o t¹o qu¶ng ninh
Tr−êng thpt chuyªn h¹ long
®Ò thi thö ®¹i häc lÇn 2"n¨m häc 2009"2010
M«n thi: to¸n" khèi a
Thêi gian lm b¸i: 180 phót
PhÇn chung cho tÊt c¶ c¸c thÝ sinh (7 ®iÓm)
C©u 1 (2 ®iÓm)
Cho hm sè
2)12(
23
−
−
+
+
−
=
mxmmxxy
, cã ®å thÞ (C
m
), trong ®ã m l tham sè.
1. Kh¶o s¸t v vÏ ®å thÞ hm sè víi m = 0
2. T×m tÊt c¶ c¸c ®iÓm cè ®Þnh m hä ®−êng cong (C
m
) ®i qua víi mäi m.
3. T×m tÊt c¶ c¸c gi¸ trÞ cña m ®Ó ®å thÞ (C
m
) c¾t trôc honh t¹i 3 ®iÓm ph©n biÖt cïng cã honh ®é
d−¬ng.
C©u 2 (2 ®iÓm)
1. Gi¶i ph−¬ng tr×nh:
xxxx 2tan.)cos(sin322sin5
22
−
=
−
2. Gi¶i bÊt ph−¬ng tr×nh:
32
27
32
32
)4(22
2
−
−
>−+
−
−
x
x
x
x
x
C©u 3 (1 ®iÓm) TÝnh tÝch ph©n:
∫
+
3
32
3
5
2
49. xx
dx
C©u 4 (1 ®iÓm)
Cho h×nh chãp S.ABC cã ®¸y l tam gi¸c ABC vu«ng c©n t¹i A. SA vu«ng gãc víi mÆt ph¼ng (ABC),
AB = a v SA =2a. Gäi M v N lÇn l−ît l h×nh chiÕu vu«ng gãc cña A trªn SB v SC. TÝnh thÓ tÝch
khèi chãp A.BCNM.
C©u 5 (1 ®iÓm)
Cho tam gi¸c ABC cã c¸c gãc tho mJn
0
90
≤
≤
≤
ABC
.
T×m gi¸ trÞ nhá nhÊt cña biÓu thøc:
2
sin.
2
sin.
2
cos BABA
M
−
=
PhÇn riªng (3®iÓm): ThÝ sinh chØ ®−îc lm mét trong hai phÇn (A hoÆc B)
A. Theo ch−¬ng tr×nh chuÈn
C©u VI.a(2®iÓm)
1. Trong mÆt ph¼ng víi hÖ to¹ ®é Oxy cho ®iÓm A(1;2) v ®iÓm B(3;5). ViÕt ph−¬ng tr×nh ®−êng trßn
ngo¹i tiÕp tam gi¸c ABO v x¸c ®Þnh to¹ ®é trùc t©m cña tam gi¸c ®ã.
2. Trong kh«ng gian víi hÖ to¹ ®é Oxyz cho c¸c ®iÓm A(U1,3,2); B(4,0,U3); C(5,U1,4) v D(0,6,1). ViÕt
ph−¬ng tr×nh tæng qu¸t cña mÆt ph¼ng (BCD). X¸c ®Þnh to¹ ®é cña h×nh chiÕu H cña A xuèng mÆt
ph¼ng (BCD).
C©u VIIa (1 ®iÓm)
Gi¶ sö sau khi khai triÓn v rót gän biÓu thøc P(x) = (2x
2
— x — 3)
8
ta ®−îc
P(x) = a
0
+ a
1
x + a
2
x
2
+ …+a
n
x
n
.
TÝnh a
4
.
B. Theo ch−¬ng tr×nh n©ng cao
C©u VI.b (2 ®iÓm)
1. Trong mÆt ph¼ng víi hÖ to¹ ®é Oxy cho ®−êng th¼ng (d
1
) : x + 2y + 3 = 0, (d
2
) : 2x — y — 2 = 0.
ViÕt ph−¬ng tr×nh ®−êng trßn (C ) tiÕp xóc víi (d
1
) v (d
2
) v ®i qua M(2,4).
2. Trong kh«ng gian víi hÖ to¹ ®é Oxyz cho mÆt ph¼ng (Q): 5x + 2y + 2z — 7 = 0 v mÆt cÇu
(C): x
2
+ y
2
+ z
2
— 2x — 4y — 6z — 67 = 0. Chøng minh r»ng: mÆt cÇu c¾t mÆt ph¼ng. X¸c ®Þnh to¹
®é t©m v tÝnh b¸n kÝnh ®−êng trßn l giao tuyÕn cña chóng.
C©u VII.b (1 ®iÓm) T×m hÖ sè cña x
35
trong khai triÓn nhÞ thøc Niut¬n cña
n
x
x
+
5
3
1
, biÕt r»ng
12...
30
12
2
12
1
12
−=+++
+++
C
C
C
n
nnn
……………HÕt……………
S¬ l−îc ®¸p ¸n v biÓu ®iÓm khèi a
C©u
Néi dung §iÓm
C©u
I
1. Kh¶o s¸t v vÏ ®å thÞ:
• TX§: R
•
−∞
=
+∞
=
−∞→+∞→
yy
xx
limlim
• Sù biÕn thiªn:
xxy
>
+
=
′
013
2
Hm sè ®ång biÕn trªn R, kh«ng cã cùc ®¹i v cùc tiÓu
x
∞
−
+
∞
y
′
+
y
• §å thÞ:
• §iÓm uèn:
00,6
=
⇔
=
′
′
=
′
′
xyxy
, râ rng
y
′
′
®æi dÊu khi qua x
= 0 nªn ®å thÞ hm sè cã ®iÓm uèn l U(0;U2)
• HS tù vÏ ®å thÞ
0,25
0,25
0,25
0,25
2.T×m tÊt c¶ c¸c ®iÓm cè ®Þnh m hä ®−êng cong (C
m
) ®i qua víi mäi m.
Gi¶ sö M(x;y) l ®iÓm cè ®Þnh m hä ®−êng cong ®i qua víi mäi m
)0;1(
0
1
0)2()1(
32
M
y
x
myxxmx
⇔
=
=
⇔
∀
=
−
−
+
−
−
⇔
0,25
0,25
3.T×m tÊt c¶ c¸c gi¸ trÞ cña m ®Ó ®å thÞ (C
m
) c¾t trôc honh t¹i 3 ®iÓm ph©n biÖt …..
Sè giao ®iÓm cña ®−êng cong víi trôc honh chÝnh l sè nghiÖm cña ph−¬ng tr×nh y =
0. Ta cã
[
]
02)1()1(0
2
=
+
+
−
+
−
⇔
=
mxmxxy
, do ®ã ycbt trë thnh: t×m m
®Ó ph−¬ng tr×nh
[
]
02)1(
2
=
+
+
−
+
mxmx
cã 2 nghiÖm ph©n biÖt kh¸c 1 v cïng
d−¬ng
7
021).1(1
01
02
076
2
>⇔
≠++−+
>−
>+
>−−=∆
⇔m
mm
m
m
mm
VËy m>7
0,25
0,25
C©u
II
1.Gi¶i ph−¬ng tr×nh:
Zk
k
xTXDxxxx ∈+≠−=−
2
4
:2tan.)cos(sin322sin5
22
π
π
.
−=
∈∈+=+=⇔=
⇔
=−+⇔−=−⇔
)(22sin
)(
12
5
;
12
5,02sin
022sin32sin22tan).2sin1(322sin5
22
Lx
TXDZkkxkxx
xxxxx
π
π
π
π
0,25
0,5
0,25
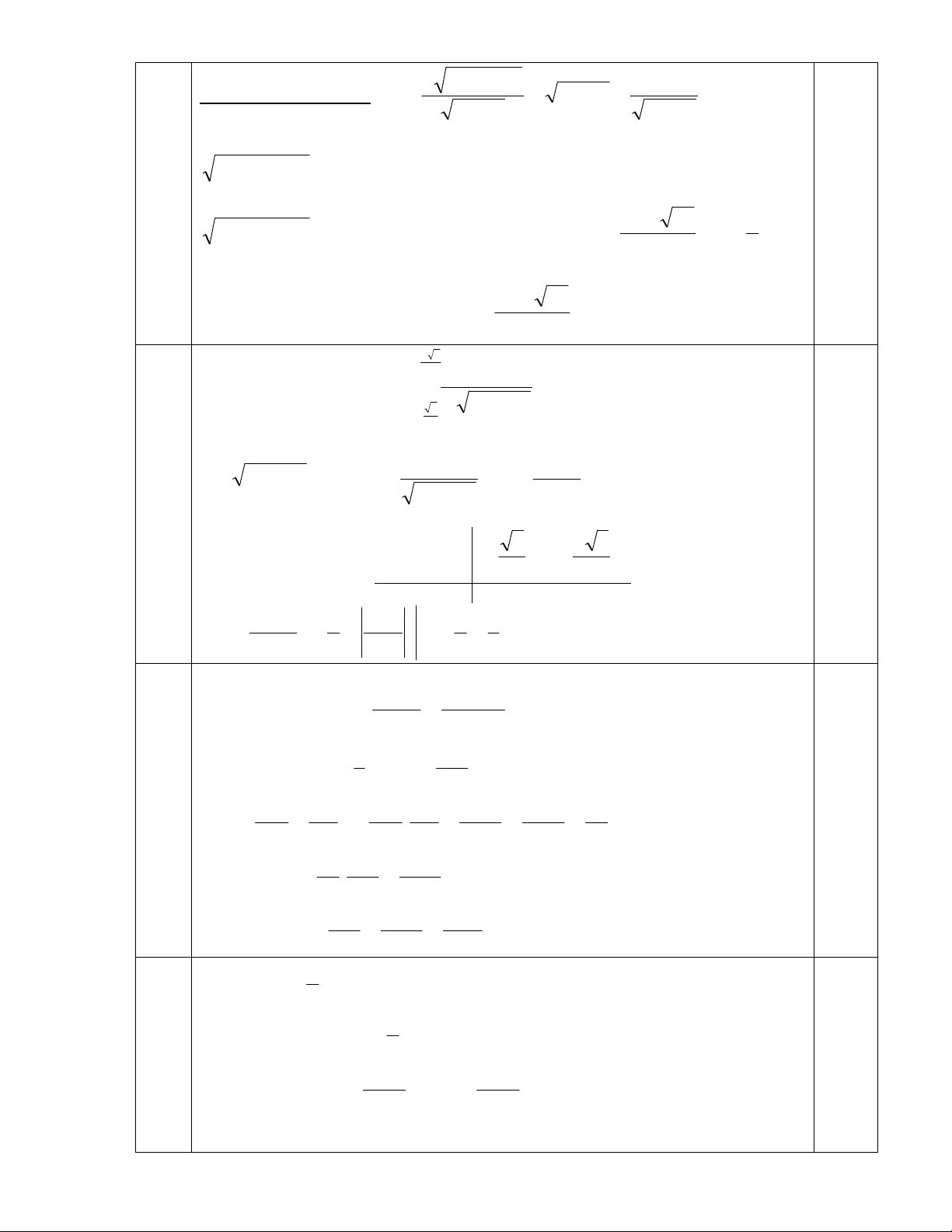
2.Gi¶i bÊt ph−¬ng tr×nh:
3
2
27
32
3
2
)4(22
2
−
−
>−+
−
−
x
x
x
x
x
§KX§:
2
≥
x
.Khi ®ã bÊt pt t−¬ng ®−¬ng víi:
⇔−>−+− xxx 2732)164(2
2
2
5
2
3410
033202
5,22
5,2
410)164(2
2
2
≤<
−
⇔
<+−
≤≤
>
⇔−>− x
xx
x
x
xx
VËy tËp nghiÖm cña bÊt ph−¬ng tr×nh l
+∞
−;
2
3410
0,5
0,5
C©u
III TÝnh tÝch ph©n:
∫
+
3
32
3
5
2
49. xx
dx
§Æt
9
4
;
49
9
49
2
2
2
2
−
=
+
=⇒=+ t
x
x
dxx
dttx
§æi cËn
x
3
5
3
32
t 3 4
I =
3
5
ln
4
1
3
4
2
2
ln
4
1
4
4
32
=
+
−
=
−
∫
t
t
t
dt
0,25
0,75
C©u
IV
Häc sinh tù vÏ h×nh
• DÔ chøng minh:
SCSB
SNSM
V
V
ABCS
AMNS
.
.
.
.
=
3
2
.2.
3
1
3
2
.
a
aaV
ABCS
==
•
25
16
25
16
.
4
4
2
2
===⇒=
a
a
SB
SM
SC
SN
SB
SM
SC
SN
SB
SM
75
52
3
2
.
25
16
33
.
aa
V
AMNS
==⇒
75
18
75
32
3
2
333
.
aaa
V
BCMNA
=−=
0,25
0,25
0,25
0,25
C©u
V BiÕn ®æi
( ) ( )
[ ]
BABAM coscoscos1
4
1+−−+=
M
( ) ( )
( )
B
C
B
A
C
A
BA
BBAAABBAC
cos.
sin
sin
cos.
sin
sin
cos
cossincossin2sin2sin
2
1
cos.sin
+=−⇒
+=+=−
0,25
0,25
Tõ gi¶ thiÕt
>≥
≥
≥
≥
⇒≤∠≤∠≤∠ 0cos;0cos
0sinsinsin
90
0
BA
CBA
ABC
1
sin
sin
sin
sin ≥≥
⇒
C
B
C
A
Nªn
(
)
BABA coscoscos
+
≥
−
4
1
≥
⇒
M
_ DÔ thÊy khi tam gi¸c ABC ®Òu th×
4
1
=
⇒
M
VËy min
4
1
≥
⇒
M
khi tam gi¸c ABC ®Òu.
0,25
0,25
C©u
VI.a
1. ViÕt ph−¬ng tr×nh ®−êng trßn ngo¹i tiÕp tam gi¸c ABO v x¸c ®Þnh to¹ ®é …..
A(1;2); B(3;5); C(0;0)
Gi¶ sö ph−¬ng tr×nh ®−êng trßn ngo¹i tiÕp tam gi¸c ABC l
022
22
=
+
−
−
+
cbyaxyx

A, B, O
∈

=
=+−−+
=+−−+
⇔
0
010653
04221
22
22
c
cba
cba
⇔
=
−=
=
⇔
5,21
5,9
0
a
b
c

:
01943
22
=
−
−
+
yxyx
Gäi H l trùc t©m cña
∆
AOB v H(a;b)
(
)
(
)
( )
=−+−
=−+−
⇔
=
=
⇔0523
02513
0.
0.
ba
ba
OABH
OBAH
=
−
=
⇔26
39
b
a
hay
(
)
26;39
−
H
0,25
0,25
0,25
0,25
2. X¸c ®Þnh to¹ ®é cña h×nh chiÕu H cña A xuèng mÆt ph¼ng (BCD).
A(U1;3;2)
B(4;0;U3)
C(5;U1;4)
D(0;6;1)
ViÕt ph−¬ng tr×nh tæng qu¸t cña mÆt ph¼ng (BCD):
+)
(
)
1;20;13
)( BCD
M
+) ph−¬ng tr×nh mÆt ph¼ng:
0
49
20
13
=
−
+
+
z
y
x
Gäi H l h×nh chiÕu cña A xuèng mÆt ph¼ng (BCD) v H(a,b,c)
AH
cïng ph−¬ng víi
)( BCD
n
=
=
=
⇒
tc
tb
ta
20
13
( )
570
49
049400169 =⇔=−++⇔∈ ttttBCDH
H
570
49
;
57
98
;
570
637
.
0,25
0,25
0,25
0,25
C©u
VII.a
P(x) =
(
)
10
2
32 −− xx
= a
0
+ a
1
x + a
2
x
2
+ …+
n
a
n
x
3
a
chÝnh l hÖ sè cña
3
x
trong khai triÓn P(x) d−íi d¹ng chÝnh t¾c
( )
( )
( )
9185403.43.
32
88
10
77
103
10
2
10
0
10
−=−=
⇒
−−=
−
=
∑
CCa
xxCxP
k
k
k
k
0,5
0,5
C©u
VI.b
2®
1. ViÕt ph−¬ng tr×nh ®−êng trßn (C ) tiÕp xóc víi (d
1
) v (d
2
) v ®i qua M(2,4)
Gi¶ sö ph−¬ng tr×nh ®−êng trßn (C) cã t©m I(a,b)
(C) tiÕp xóc víi d
1
, d
2
v ®i qua M(2;4)
(
)
(
)
IMdIddId
=
=
⇔
21
;;
( ) ( )
( ) ( ) ( )
[
)
( )
( )
( ) ( ) ( )
[ ]
( )
−+−=++
−−−=++
−+−=++
−−=++
⇔
−+−=
−−
=
++
⇔
2
42532
2232
1
42532
2232
42
5
22
5
32
222
222
22
baba
baba
baba
baba
ba
baba
* XÐt (1): ta thÊy kh«ng cã gi¸ trÞ a, b tho¶ mJn
* XÐt (2) ta ®−îc :
−
=
+−
=
5
31637
5
31214
b
a
hoÆc
+
=
−−
=
5
31637
5
31214
b
a
VËy cã hai ®−êng trßn tho¶ mJn:
( )
( )
25
313001237
5
31637
5
31214
:
25
313001237
5
31637
5
31214
:
22
2
22
1
−
=
−
−+
+−
−
+
=
+
−+
+
+
yxC
yxC
0,5
0,5
2.Chøng minh r»ng: mÆt cÇu c¾t mÆt ph¼ng . X¸c ®Þnh to¹ ®é t©m v tÝnh b¸n kÝnh…..
MÆt cÇu (C) cã t©m I(1;2;3) v b¸n kÝnh b»ng 9.
( )( )
9
33
8
225
73.22.21.5
;
222
<=
++
−
+
+
=QId
MÆt ph¼ng c¾t mc
Gäi b¸n kÝnh ®−êngtrßn giao tuyÕn l
33
2609
33
8
9
2
2//
=
−=⇒RR
T©m ®−êng trßn l
(
)
IIcbaI ⇒,,
/
/
cïng ph−¬ng Q
n
(5,2,2)
=
=
=
⇒
tc
tb
ta
2
2
5
v
⇒
=⇔∈
33
14
;
33
14
;
33
35
33
7
//
ItQI
0,5
0,5