LUYỆN THI ðẠI HỌC LOPLUYENTHI.COM
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH
Câu I (2 ñiểm) Cho hàm số
2x 3
y
x 2
−
=−có
ñồ
th
ị
(C).
1.
Kh
ả
o sát s
ự
bi
ế
n thiên và v
ẽ
ñồ
th
ị
c
ủ
a hàm s
ố
(C)
2.
Tìm trên (C) nh
ữ
ng
ñ
i
ể
m M sao cho ti
ế
p tuy
ế
n t
ạ
i M c
ủ
a (C) c
ắ
t hai ti
ệ
m c
ậ
n c
ủ
a (C) t
ạ
i A, B
sao cho AB ng
ắ
n nh
ấ
t.
Câu II
(2
ñ
i
ể
m)
1.
Gi
ả
i ph
ươ
ng trình: 2( tanx – sinx ) + 3( cotx – cosx ) + 5 = 0
2.
Gi
ả
i ph
ươ
ng trình: x
2
– 4x - 3 =
x 5
+
Câu III
(1
ñ
i
ể
m) Tính tích phân:
√1
√
Câu IV
(1
ñ
i
ể
m)
Kh
ố
i chóp tam giác SABC có
ñ
áy ABC là tam giác vuông cân
ñỉ
nh C và SA vuông góc v
ớ
i m
ặ
t
ph
ẳ
ng (ABC), SC = a. Hãy tìm góc gi
ữ
a hai m
ặ
t ph
ẳ
ng (SCB) và (ABC)
ñể
th
ể
tích kh
ố
i chóp l
ớ
n nh
ấ
t.
Câu V
(1
ñ
i
ể
m)
Cho x, y, z là các s
ố
d
ươ
ng th
ỏ
a mãn 1 1 1
4
x y z
+ + =
. CMR: 1 1 1
1
222x y z x y z x y z
+ + + + + +
PHẦN TỰ CHỌN: Thí sinh chọn một trong hai phần A hoặc B
A. Theo chương trình Chuẩn
Câu VI.a.( 2 ñiểm )
1
. Tam giác cân ABC có
ñ
áy BC n
ằ
m trên
ñườ
ng th
ẳ
ng : 2x – 5y + 1 = 0, c
ạ
nh bên AB n
ằ
m trên
ñườ
ng th
ẳ
ng : 12x – y – 23 = 0 . Vi
ế
t ph
ươ
ng trình
ñườ
ng th
ẳ
ng AC bi
ế
t r
ằ
ng nó
ñ
i qua
ñ
i
ể
m (3;1)
2.
Trong không gian v
ớ
i h
ệ
t
ọ
a
ñộ
ð
êcác vuông góc Oxyz cho mp(P):
x – 2y + z – 2 = 0 và hai
ñườ
ng th
ẳ
ng :
(d)
x 1 3 y z 2
1 1 2
+ − +
= =
− và (d’)
x 1 2t
y 2 t
z 1 t
= +
= +
= +
Vi
ế
t ph
ươ
ng trình tham s
ố
c
ủ
a
ñườ
ng th
ẳ
ng (
∆
) n
ằ
m trong m
ặ
t ph
ẳ
ng (P) và c
ắ
t c
ả
hai
ñườ
ng
th
ẳ
ng (d) và (d’). CMR (d) và (d’) chéo nhau và tính kho
ả
ng cách gi
ữ
a chúng.
Câu VIIa
. ( 1
ñ
i
ể
m )
Tính t
ổ
ng :
0 5 1 4 2 3 3 2 4 1 5 0
5 7 5 7 5 7 5 7 5 7 5 7
S C C C C C C C C C C C C
= + + + + +
B. Theo chương trình Nâng cao
Câu VI.b.( 2 ñiểm )
1. Vi
ế
t ph
ươ
ng trình ti
ế
p tuy
ế
n chung c
ủ
a hai
ñườ
ng tròn :
(C
1
) : (x - 5)
2
+ (y + 12)
2
= 225 và (C
2
) : (x – 1)
2
+ ( y – 2)
2
= 25
2. Trong không gian v
ớ
i h
ệ
t
ọ
a
ñộ
ð
êcác vuông góc Oxyz cho hai
ñườ
ng th
ẳ
ng:
(d)
x t
y 1 2t
z 4 5t
=
= +
= +
và (d’)
x t
y 1 2t
z 3t
=
= − −
= −
a. CMR hai
ñườ
ng th
ẳ
ng (d) và (d’) c
ắ
t nhau.
b. Vi
ế
t ph
ươ
ng trình chính t
ắ
c c
ủ
a c
ặ
p
ñườ
ng th
ẳ
ng phân giác c
ủ
a góc t
ạ
o b
ở
i (d) và (d’).
Câu VIIb.
( 1
ñ
i
ể
m )
Gi
ả
i ph
ươ
ng trình :
(
)
5
log x 3
2 x
+
=
----------------------------- H
ế
t -----------------------------
LOPLUYENTHI.COM ðỀ THI THỬ ðẠI HỌC LẦN 5 NĂM 2010
TVE MÔN THI: TOÁN
Thời gian làm bài 180 phút (không kể thời gian giao ñề)
LUY
ỆN THI
ð
ẠI HỌC
LOPLUYENTHI.COM
®¸p ¸n ®Ò thi thö ®¹i häc lÇn
2
n¨m häc 2009
-
2010
M«n thi: to¸n
Thêi gian lµm bµi: 180 phót, kh«ng kÓ thêi gian giao ®Ò
C©u Néi dung §iÓm
I
2.0®
1
1.25®
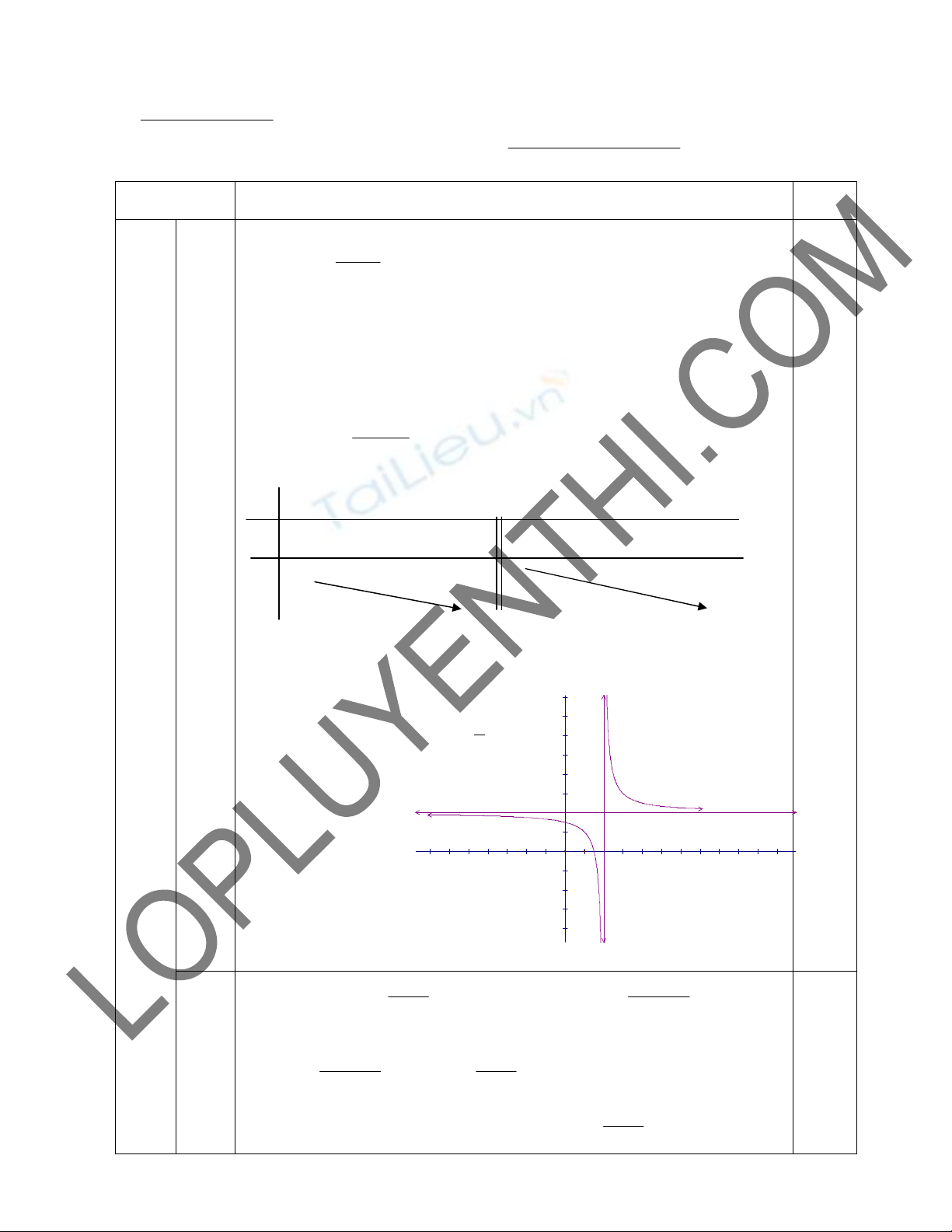
Hµm sè y =
2x 3
x 2
−
−
cã :
- TX§: D =
R
\ {2}
- Sù biÕn thiªn:
+ ) Giíi h¹n :
x
Lim y 2
→∞
=
. Do ®ã §THS nhËn ®−êng th¼ng y = 2 lµm TCN
,
x 2 x 2
lim y ; lim y
− +
→ →
= −∞ = +∞
. Do ®ã §THS nhËn ®−êng th¼ng x = 2 lµm TC§
+) B¶ng biÕn thiªn:
Ta cã : y’ =
( )
2
1
x 2
−−
< 0
x D∀ ∈
Hµm sè nghÞch biÕn trªn mçi kho¶ng
( )
−∞;2
vµ hµm sè kh«ng cã cùc trÞ
- §å thÞ
+ Giao ®iÓm víi trôc tung : (0 ;
3
2
)
+ Giao ®iÓm víi trôc hoµnh :
A(3/2; 0)
- §THS nhËn ®iÓm (2; 2)
lµm t©m ®èi xøng
0,25
0,25
0,25
0,5
2
0,75
ñ
L
ấ
y
ñ
i
ể
m
1
M m;2 m 2
+
−
( )
C∈
. Ta có :
( ) ( )
2
1
y' m m 2
= − −
.
Ti
ế
p tuy
ế
n (d) t
ạ
i M có ph
ươ
ng trình :
( ) ( )
2
1 1
y x m 2 m 2
m 2
= − − + + −
−
Giao
ñ
i
ể
m c
ủ
a (d) v
ớ
i ti
ệ
m c
ậ
n
ñứ
ng là :
2
A 2;2 m 2
+
−
0,25
ñ
0,25
ñ
8
6
4
2
-2
-4
-5
5 10
y’
y
x
+∞
−∞
-
+∞
−∞
2
-
2
2
2
LUY
Ệ
N THI
ðẠ
I H
Ọ
C LOPLUYENTHI.COM
Giao
ñ
i
ể
m c
ủ
a (d) v
ớ
i ti
ệ
m c
ậ
n ngang là : B(2m – 2 ; 2)
Ta có :
( ) ( )
2
22
1
AB 4 m 2 8
m 2
= − + ≥
−
. D
ấ
u “=” x
ả
y ra khi và ch
ỉ
khi
( ) ( )
2
2
m 3
1
m 2
m 1
m 2
=
− = ⇔
=
−
V
ậ
y
ñ
i
ể
m M c
ầ
n tìm có t
ọ
a
ñộ
là : (3; 3); (1; 1)
0,25
ñ
II
2,0®
1
1,0®
Ph
ươ
ng
tr
ình
ñ
ã
cho t
ươ
ng
ñươ
ng v
ớ
i
:
2(tanx + 1 – sinx) + 3(cotx + 1 – cosx) = 0
( ) ( )
sin x cosx
2 1 sin x 1 cosx 0
cosx sin x
2 sin x cosx cosx.sin x 3 sin x cosx cosx.sin x
0
cosx sin x
⇔ + − + + − =
+ − + −
⇔ + =
( )
2 3
cosx sin x cosx.sin x 0
cosx sin x
⇔ + + − =
•
Xét 2 3 3
0 tan x tan x
cosx sin x 2
−
+ = ⇔ = = α ⇔ = α + π
k
•
Xét : sinx + cosx – sinx.cosx = 0 .
ðặ
t t = sinx + cosx
v
ớ
i
t 2; 2
∈ −
. Khi
ñ
ó ph
ươ
ng trình tr
ở
thành:
22
t 1
t 0 t 2t 1 0 t 1 2
2
−
− = ⇔ − − = ⇔ = −
Suy ra :
1 2
2cos x 1 2 cos x cos
4 4 2
π π −
− = − ⇔ − = = β
x 2
4
π
⇔ = ±β+ π
k
0,25
0,25
0,5
2
1,0®
x
2
- 4x + 3 =
x 5
+
(1)
TX§ : D =
[
5; )
− +∞
( ) ( )
2
1 x 2 7 x 5
⇔ − − = +
®Æt y - 2 =
x 5
+
,
( )
2
y 2 y 2 x 5
≥⇒− = +
Ta cã hÖ :
( )
( ) ( )
( )( )
22
2
x 2 y 5 x 2 y 5
y 2 x 5 x y x y 3 0
y 2 y 2
− = + − = +
− = + ⇔ − + + =
≥ ≥
( )
( )
2
2
x 2 y 5
x y 0
5 29
x2
x 2 y 5 x 1
x y 3 0
y 2
− = +
− =
+
=
⇔ ⇔
− = +
= −
+ + =
≥
0,25
0,25
0,5
III
1.0® 1®
ðặ
t t = x +
2
x 1
+
( )
2 2
2
2
2
t 1 t 1
x 1 t x x dx dt
2t 2t
− +
⇒+ = − ⇒=⇒=
ðổ
i c
ậ
n : Khi x = -1 thì t =
2 1
−
và khi x = 1 thì t =
2 1
+
.
0,5
LUY
Ệ
N THI
ð
Ạ
I H
Ọ
C
LOPLUYENTHI.COM
Do
ñ
ó
:
( )
2 1 2 1
2
2 2
2 1 2 1
1 t 1 1 1 1 2
I dt dt
2 t t 1 2 t t t 1
+ +
− −
+
= = − +
+ +
∫ ∫
2 1
2 1
1 1 ln t 2ln t 1 | 1
2 t
+
−
= − − + + =
0,5
IV
2®
1.0®
G
ọ
i
ϕ
là góc gi
ữ
a hai mp (SCB) và (ABC) .
Ta có :
SCA
ϕ =
; BC = AC = a.cos
ϕ
; SA = a.sin
ϕ
V
ậ
y
( )
3 2 3 2
SABC ABC
1 1 1 1
V .S .SA .AC.BC.SA a sin .cos a sin 1 sin
3 6 6 6
= = = ϕ ϕ = ϕ − ϕ
Xét hàm s
ố
: f(x) = x – x
3
trên kho
ả
ng ( 0; 1)
Ta có : f’(x) = 1 – 3x
2
.
( )
1
f ' x 0 x 3
= ⇔ = ±
T
ừ
ñ
ó ta th
ấ
y trên kho
ả
ng (0;1) hàm s
ố
f(x) liên t
ụ
c và có m
ộ
t
ñ
i
ể
m c
ự
c tr
ị
là
ñ
i
ể
m
c
ự
c
ñạ
i, nên t
ạ
i
ñ
ó hàm s
ố
ñạ
t GTLN
hay
( )
( )
x 0;1
1 2
Maxf x f 3 3 3
∈
= =
V
ậ
y MaxV
SABC
=
3
a
9 3
,
ñạ
t
ñượ
c khi
sin
ϕ
=
1
3
hay
1
arcsin 3
ϕ =
( v
ớ
i 0 <
2
π
ϕ <
)
0,25
0,5
V 1.0®
+Ta có :
1 1 1 1
2 4 2
.( )
x y z x y z
≤ +
+ + +
;
1 1 1 1
2 4 2
( )
x y z y x z
≤ +
+ + +
;
1 1 1 1
2 4 2
( )
x y z z y x
≤ +
+ + +
+ L
ạ
i có :
1 1 1 1
( );
x y 4 x y
≤ +
+
1 1 1 1
( );
y z 4 y z
≤ +
+
1 1 1 1
( );
x z 4 x z
≤ +
+
c
ộ
ng các B
ð
T này ta
ñượ
c
ñ
pcm.
1®
VIa
2®
1
1®
ðườ
ng th
ẳ
ng AC
ñ
i qua
ñ
i
ể
m (3 ; 1) nên có ph
ươ
ng trình :
a(x – 3) + b( y – 1) = 0 (a
2
+ b
2
≠
0). Góc c
ủ
a nó t
ạ
o v
ớ
i BC b
ằ
ng góc c
ủ
a
AB t
ạ
o v
ớ
i BC nên:
2 2 2 2 2 2 2 2
2a 5b 2.12 5.1
2 5 . a b 2 5 . 12 1
− +
=
+ + + +
2 2
2a 5b 29
5
a b
−
⇔ =
+
( )
( )
22 2
5 2a 5b 29 a b⇔ − = +
0,25
0,25
0,25
A
B
C
S
ϕ
LUY
Ệ
N THI
ðẠ
I H
Ọ
C LOPLUYENTHI.COM
⇔
9a
2
+ 100ab – 96b
2
= 0
a 12b
8
a b
9
= −
⇒=
Nghi
ệ
m a = -12b cho ta
ñườ
ng th
ẳ
ng song song v
ớ
i AB ( vì
ñ
i
ể
m ( 3 ; 1)
không thu
ộ
c AB) nên không ph
ả
i là c
ạ
nh tam giác .
V
ậ
y còn l
ạ
i : 9a = 8b hay a = 8 và b = 9
Ph
ươ
ng trình c
ầ
n tìm là : 8x + 9y – 33 = 0
0,25
2
1®
M
ặ
t ph
ẳ
ng (P) c
ắ
t (d) t
ạ
i
ñ
i
ể
m A(10 ; 14 ; 20) và c
ắ
t (d’) t
ạ
i
ñ
i
ể
m B(9 ; 6 ; 5)
ðườ
ng th
ẳ
ng
'
c
ầ
n tìm
ñ
i qua A, B nên có ph
ươ
ng trình:
x 9 t
y 6 8t
z 5 15t
= −
= −
= −
+
ðườ
ng th
ẳ
ng (d)
ñ
i qua M(-1;3 ;-2) và có VTCP
(
)
u 1;1;2
v
+
ðườ
ng th
ẳ
ng (d’)
ñ
i qua M’(1 ;2 ;1) và có VTCP
(
)
u' 2;1;1
uur
Ta có :
•
(
)
MM' 2; 1;3
= −
uuuuur
•
( )
(
)
1 2 2 1 1 1
1 1 1 2 2 1
MM' u,u' 2; 1;3 ; ; 8 0
= − = − ≠
uuuuur r uur
Do
ñ
ó (d) và (d’) chéo nhau .(
ð
pcm)
Khi
ñ
ó :
( ) ( )
( )
MM' u,u '
8
d d , d'
11
u,u'
= =
uuuuur r uur
r uur
0,25
0,25
0,25
0,25
VIIa
1
ñ
Ch
ọ
n
khai tri
ể
n
:
( )
5
0 1 2 2 5 5
5 5 5 5
x 1 C C x C x C x
+ = + + + +L
( )
70 1 2 2 7 7 0 1 2 2 5 5
7 7 7 7 7 7 7 7
x 1 C C x C x C x C C x C x C x
+ = + + + + = + + + + +
L L L
H
ệ
s
ố
c
ủ
a x
5
trong khai tri
ể
n c
ủ
a (x + 1)
5
.(x + 1)
7
là:
0 5 1 4 2 3 3 2 4 1 5 0
5 7 5 7 5 7 5 7 5 7 5 7
C C C C C C C C C C C C
+ + + + +
M
ặ
t khác : (x + 1)
5
.(x + 1)
7
= (x + 1)
12
và h
ệ
s
ố
c
ủ
a x
5
trong khai tri
ể
n c
ủ
a
(x + 1)
12
là :
5
12
C
T
ừ
ñ
ó ta có :
0 5 1 4 2 3 3 2 4 1 5 0
5 7 5 7 5 7 5 7 5 7 5 7
C C C C C C C C C C C C
+ + + + +
=
5
12
C
= 792
.0,25
0,25
0,25
0,25