http://ebook.here.vn – Download Bài giảng – ðề thi miễn phí
Trường THPT Nguyễn Huệ
ðỀ THI THỬ ðẠI HỌC LẦN I, NĂM 2011
Môn: TOÁN; Khối: A, B
(Thời gian làm bài 180 phút)
A. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7 ñiểm)
Câu I. (2 ñiểm) . Cho hàm số
2 4
1
x
y
x
−
=
−
1.Khảo sát và vẽ ñồ thị hàm số (C)
2.Viết phương trình tiếp tuyến của (C) sao cho khoảng cách từ giao ñiểm hai tiệm cận ñến tiếp
tuyến là lớn nhất
Câu II
(2 ñiểm)
1. Giải phương trình:
sin 4 cos4 4 2 sin ( ) 1
4
x x x
π
+ = + −
.
2. Giải phương trình:
( )
4 3 2
3 4 1 1
x x x
− = − +
Câu III
(1 ñiểm)
Tính tích phân:
3
3
2
1
log
1 3ln
e
x
I dx
x x
=+
∫
.
Câu IV
. (1 ñiểm)
Cho hình hộp ñứng ABCD.A'B'C'D' có AB = AD = 2a, AA' =
3
a
và góc BAD = 60
0
. gọi M và
N là trung ñiểm các cạnh A'D' và A'B'. Tính thể tích khối chóp A.BDMN.
Câu V:
(1 ñiểm) Cho x,y,z là các số thực không âm. Tìm giá trị lớn nhất của
( )( )( )
1 1
1 1 1 1
P
x y z x y z
= −
+ + + + + +
B. PHẦN RIÊNG
(3 ñiểm). Thí sinh chỉ ñược làm một trong hai phần (phần 1 hoặc 2)
1.Theo chương trình Chuẩn
Câu VIa.
( 2 ñiểm)
1. Trong mặt phẳng với hệ tọa ñộ Oxy, cho ñường tròn (C): x
2
+ y
2
- 2x - 2my + m
2
- 24 = 0 có tâm
I và ñường thẳng
∆
: mx + 4y = 0. Tìm m biết ñường thẳng
∆
cắt ñường tròn (C) tại hai ñiểm phân
biệt A,B thỏa mãn diện tích tam giác IAB bằng 12.
2.Giải bất phương trình
2
2 2
1 1 2
1 1
2 2
2
x x
x x
x
− −
− ≥ −
Câu VIIa
. (1 ñiểm).Cho hàm số y = - x
3
+ 3mx
2
-3m – 1. Với giá trị nào của m thì ñồ thị hàm số có
ñiểm cực ñại, ñiểm cực tiểu ñối xứng với nhau qua ñường thẳng d: x + 8y – 74 = 0.
2. Theo chương trình Nâng cao
Câu VIb.
( 2 ñiểm).
1.Trong hệ tọa ñộ Oxy, cho ñiểm A(3; 2), các ñường thẳng
∆1
: x + y – 3 = 0 và ñường thẳng
∆2
: x + y – 9 = 0. Tìm tọa ñộ ñiểm B thuộc
∆1
và ñiểm C thuộc
∆2
sao cho tam giác ABC vuông cân
tại A.
2. Giải hệ phương trình:
−=−
−=+
1)(log
2
2
yxy
yyxx
Câu VIIb
. (1 ñiểm)
Cho hàm số (C
m
):
2
1
x x m
y
x
− +
=−
(m là tham số). Tìm m ñể (C
m
) cắt Ox tại hai ñiểm phân biệt
A,B sao cho tiếp tuyến của (C
m
) tại A, B vuông góc.
http://ebook.here.vn – Download Bài giảng – ðề thi miễn phí
A. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7.0 ñiểm)
CÂU NỘI DUNG THANG
ðIỂM
TXð : D = R\{1}
0.25
Chiều biến thiên
lim ( ) lim ( ) 2
x x
f x f x
→+∞ →−∞
= = −
nên y = - 2 là tiệm cận ngang của ñồ thị hàm số
1 1
lim ( ) , lim
x x
f x
+ −
→ →
= +∞ = −∞
nên x = 1 là tiệm cận ñứng của ñồ thị hàm số
y’ =
2
2
0
(1 )x
− <
−,
1
x
∀ ≠
0.25
Bảng biến thiên
Hàm số nghịc biến trên
( ;1)
−∞
và
(1; )
+∞
Hàm số không có cực trị
0.25
ðồ thị.(tự vẽ)
Giao ñiểm của ñồ thị với trục Ox là (0 ;- 4)
Vẽ ñồ thị
Nhận xét : ðồ thị nhận giao ñiểm của 2 ñường tiệm cận I(1 ;-2) làm tâm ñối xứng
0.25
Ta có d(I;
∆
) =
0
2
0
4 2
0 0
4
14
4 4
1 (1 )
(1 ) (1 )
x
x
x x
−=
+ + −
− −
Ta có
2
0
2
2
0
0
2
0
4 4
(1 ) 4 2
(1 ) 4(1 )
(1 )
x
xx
x
+ − ≥ ⇒ ≤
−+ −
−
0.25
Dấu bằng xảy ra khi
0
0
1 2
1 2
x
x
= −
= +
0.25
Câu I
(2.0ñ)
1. (1.0ñ)
2. (1.0ñ)
+ Với
0
1 2
x= −
ta có tiếp tuyến là y = - x -1
2 2
−
+ Với
0
1 2
x= +
ta có tiếp tuyến là y = - x -1
2 2
+
0.25
Câu
II(2.0ñ)
PT ⇔ 2sin 2x cos 2x + 2cos
2
2x = 4(sin x + cos x)
⇔ (cos x + sin x) (cos x – sin x) (sin 2x + cos 2x) = 2(sin x + cos x)
⇔
sinx cos 0
(cos sinx)(sin 2 os2 ) 2
x
x x c x
+ =
− + =
0.25
http://ebook.here.vn – Download Bài giảng – ðề thi miễn phí
⇔ 4
os3 sinx 2
x k
c x
ππ
= − +
− =
0.25
1. (1.0ñ)
Chứng minh ñược phương trình cos 3x + sin x = 2 vô nghiệm
KL: x =
4
k
π
π
− +
0.25
2.(1.0ñ)
( )( )
(
)
2 2 2
4 3 2 2 2 4 3
2
2 2
2
2
1 2
3 4 1 1 1 2 3 4 1 1
0
1 2
3 4 1 1
x x x
x x x x x x x
x
x
x x
x x
x
− + + +
− = − + + + + ⇔ − = + +
=
⇔+ + +
− =
+ +
( )
2 2 2 2
2
2
2 2
1 2 3 2 1
3 4 3 2 0
1 1 1 1
x x x x
x x x
x x
+ + + + − +
− = ⇔ − + =
+ + + +
Ta có
( )
2 2
2
2 2
2
3 2 1
3 2 1 0, 3 2 0
1 1
x x
x x x x
x
+ − +
+ − + > ∀ ⇒ − + =
+ +
vô nghiệm
Vậy phương trình ñã cho có 1 nghiệm duy nhất x = 0
0.25
0.25
0.25
0.25
ðặt
2 2 2
1 1
1 3ln ln ( 1) ln .
3 3
dx
x t x t x tdt
x
+ = ⇒ = − ⇒ = . ðổi cận …
0.25
Suy ra
( ) ( )
2
2 2
3
2
3
3 3
2
1 1 1
11
log 1 1 1
3
. 1
ln 3 3 9ln 3
1 3ln
e
t
x
I dx tdt t dt
t
x x
−
= = = −
+
∫ ∫ ∫
0.25
2
3
3 3
1
1 1 4
9ln 3 3 27ln 3
t t
= − =
0.25
http://ebook.here.vn – Download Bài giảng – ðề thi miễn phí
Câu IV.
(1.0ñ)
J
I
P
N
M
D'
C'
B'
A'
D
C
B
A
Chứng minh AP là ñường cao của khối chóp A.BDMN.
Tính diện tích hình thang MNDB là
( ) ( )
2
2 15
IJ
3 15
2
2 2 4
a
a a
MN DB a
S
+
+
= = =
ðộ dài ñường cao 2 2
15
5 5
a
AP AC= =
Vậy thể tích khối chóp A.BDMN. là
2
3
1 2 3 15 3
15
3 5 4 2
a a
V a
= = (ñơn vị thể tích)
0,25
0,25
0,25
0,25
( )
3
1 27
1
3
Px y z x y z
≤ −
+ + + + + +
0.25
ðặt t = x + y + z,
0
t
≥
, xét hàm số
( )
3
1 27
( ) 13
f t t
t
= −
++,
0
t
≥
( )
4
0
1 81
'( ) , '( ) 0
3
13
t
f t f t
t
tt
=
= − + = ⇔
=
++
Lập bảng biến thiên
.
0.25
0.25
Câu V.
(1.0ñ)
ta có MaxP = Max
( )
f t
=
f(3) =
1
8
.
ðạt ñược khi x = y = y = 1
0.25
B. PHẦN RIÊNG (3 ñiểm)
Câu VIa.
(2.0ñ)
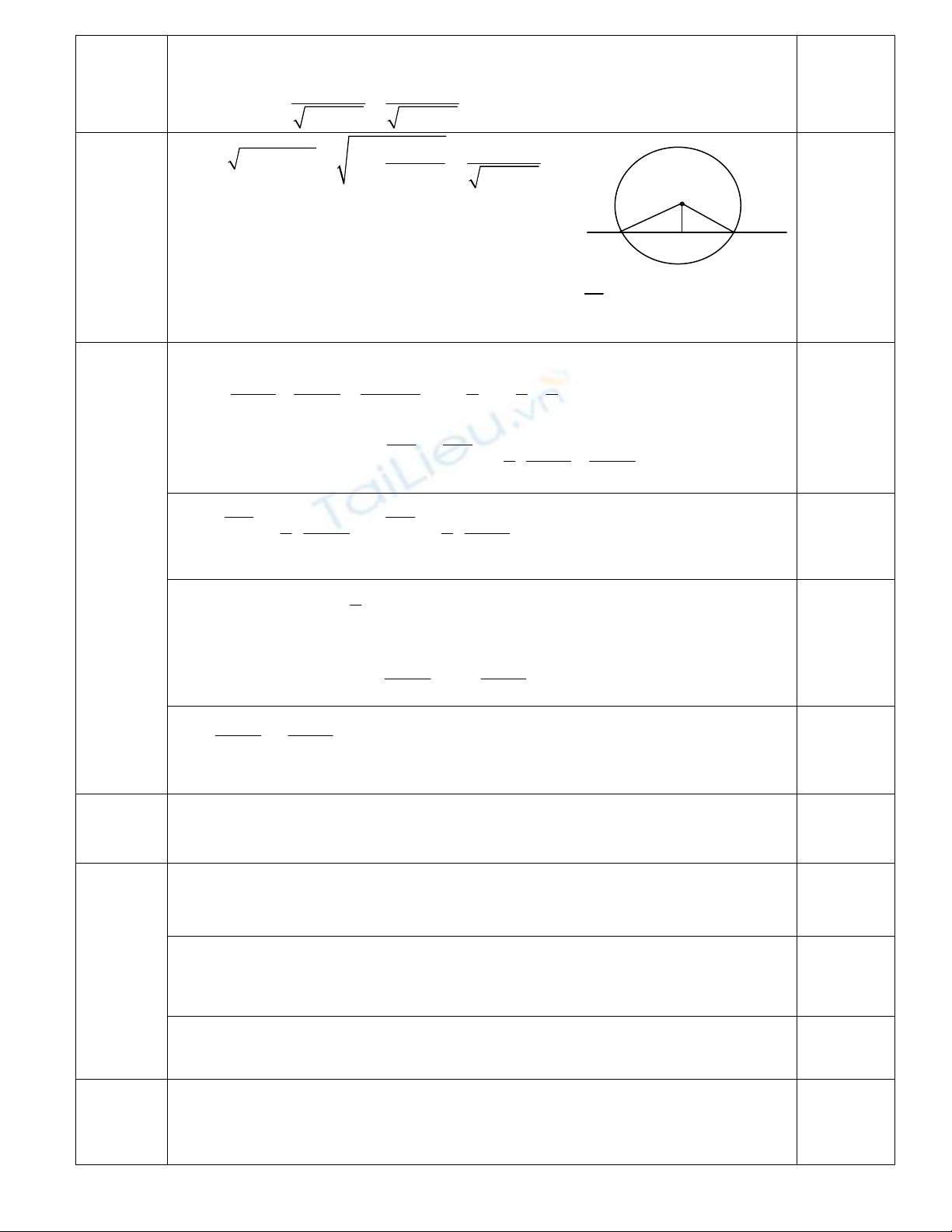
ðường tròn (C) có tâm I(1; m), bán kính R = 5.
http://ebook.here.vn – Download Bài giảng – ðề thi miễn phí
1. (1.0ñ)
Gọi H là trung ñiểm của dây cung AB.
Ta có IH là ñường cao của tam giác IAB.
IH =
2 2
| 4 | | 5 |
( , )
16 16
m m m
d I
m m
+
∆ = =
+ +
0.25
2
2 2
22
(5 ) 20
25 16
16
m
AH IA IH mm
= − = − =
++
Diện tích tam giác IAB là
12 2 12
S
IAB IAH
S
∆ ∆
= ⇔ =
⇔
2
3
( , ). 12 25 | | 3( 16)
16
3
m
d I AH m m m
= ±
∆ = ⇔ = + ⇔
= ±
0.25
0.25
0.25
ðiều kiện: x ≠ 0
Ta có:
2
2
2
2
2
2121
x
xx
x
x
x
x−
=
−
−
−= 1 -
x
2= 2( )
1
2
1
x
−
Phương bất trình có dạng: 2
2
2
1
x
x−
- 2
2
21
x
x−
≥
−
−
−
2
2
2
121
2
1
x
x
x
x
0.25
<=> 2
2
2
1
x
x−
+
2
1.
2
2
1
x
x−
≥
2
2
21
x
x−
+
2
1.
2
21
x
x
−
0.25
Xét hàm số: f(t) = 2
t
+
2
1t
Hàm số ñồng biến.
Vậy bất phương có dạng: f(
2
2
1
x
x−)
≥
f(
2
21
x
x
−
)
0.25
2. (1.0ñ)
<=>
2
2
1
x
x−
≥
2
21
x
x
−
<=> - x
2
+ 2x
≥
0 <=>
0 2
x
≤ ≤
Vậy tập nghiệm của bất phương trình là S =
(
]
0;2
0.25
Câu VIIa
(1.0ñ)
Ta có y’ = - 3x
2
+ 6mx ; y’ = 0 ⇔ x = 0 v x = 2m.
Hàm số có cực ñại , cực tiểu ⇔ phương trình y’ = 0 có hai nghiệm phân biệt ⇔
m ≠ 0.
0,25
Hai ñiểm cực trị là A(0; - 3m - 1) ; B(2m; 4m
3
– 3m – 1)
Trung ñiểm I của ñoạn thẳng AB là I(m ; 2m
3
– 3m – 1)
Vectơ
3
(2 ;4 )
AB m m
=
uuur
; Một vectơ chỉ phương của ñường thẳng d là
(8; 1)
u
= −
r
.
0,25
Hai ñiểm cực ñại , cực tiểu A và B ñối xứng với nhau qua ñường thẳng d ⇔
I d
AB d
∈
⊥
0,25
⇔
3
8(2 3 1) 74 0
. 0
m m m
AB u
+ − − − =
=
uuur r ⇔
m = 2 0,25
Câu VIa.
(2.0ñ)
B ∈ ∆
1
⇔ B(a; 3 –a) . C ∈ ∆
2
⇔ C(b; 9-b)
∆ ABC vuông cân tại A ⇔
2 2
. 0
AB AC
AB AC
=
=
uuur uuur
0,25
I
A
B
∆
∆∆
∆
H
5