Đ THI VÀ G I Ý BÀI GI I Ề Ợ Ả
MÔN TOÁN –ĐH-CĐ năm 2011
***
PH N CHUNG CHO T T C CÁC THÍ SINHẦ Ấ Ả
Câu I (2 đi m). Cho hàm s y = ể ố
2
x mx 2m 1
mx 1
− + −
−
(1), có đ th là (Cồ ị m), m là tham
s .ố
1. Kh o sát s bi n thiên và v đ th c a hàm s (1) khi m = 1.ả ự ế ẽ ồ ị ủ ố
2. Xác đ nh m đ ti m c n xiên c a (Cị ể ệ ậ ủ m) đi qua g c t a đ và hàm s (1) có c c tr .ố ọ ộ ố ự ị
Câu II (2 đi m)ể
1. Gi i ph ng trình : ả ươ
2 2
2 3 sin x
sin x sin x
3 3 2
π π −
� � � �
+ + + =
� � � �
� � � �
2. Cho h ph ng trình : ệ ươ
3 3
x y m(x y)
x y 2
+ = +
− =
Tìm t t c các giá tr c a m đ h ph ng trình trên có 3 nghi m phân bi t (xấ ả ị ủ ể ệ ươ ệ ệ 1;
y1), (x2; y2) và (x3; y3) sao cho x1, x2, x3 l p thành m t c p s c ng.ậ ộ ấ ố ộ
Câu III (2 đi m). 1.ểTam giác ABC có a = b
2
- Ch ng minh r ng : cosứ ằ 2A = cos2B.
- Tìm giá tr l n nh t c a góc B và giá tr t ng ng c a các góc A, C.ị ớ ấ ủ ị ươ ứ ủ
2. Tính tích phân: I =
3
2
1
ln x dx
(x 1)
+
Câu IV (2 đi m). ể
Trong không gian v i h t a đ Oxyz, cho ba đi m A (6;-2;3); B (2;-1;3); C (4;0;-ớ ệ ọ ộ ể
1).
1. Ch ng minh r ng: A, B, C là ba đ nh c a m t tam giác. Tìm đ dài đ ng caoứ ằ ỉ ủ ộ ộ ườ
c a tam giác ABC k t đ nh A.ủ ẻ ừ ỉ
2. Tìm m và n đ đi m M (m + 2; 1; 2n + 3) th ng hàng v i A và C.ể ể ẳ ớ
PH N T CH N: Thí sinh ch đ c ch n làm câu V. a ho c câu V.bẦ Ự Ọ ỉ ượ ọ ặ
Câu V.a. Theo ch ng trình THPT không phân ban ươ (2 đi m)ể
1. Trong m t ph ng v i h t a đ Oxy, cho hypebol (H) có ph ng trình:ặ ẳ ớ ệ ọ ộ ươ
2 2
x y 1
2 3
− =
và đi m M(2; 1). Vi t ph ng trình đ ng th ng d đi qua M, bi tể ế ươ ườ ẳ ế
r ng đ ng th ng đó c t (H) t i hai đi m A, B mà M là trung đi m c a AB.ằ ườ ẳ ắ ạ ể ể ủ
2. Cho hai đ ng th ng song song. Trên đ ng th ng th nh t l y 9 đi m phânườ ẳ ườ ẳ ứ ấ ấ ể
bi t. Trên đ ng th ng th hai l y 16 đi m phân bi t. H i có bao nhiêu tam giácệ ườ ẳ ứ ấ ể ệ ỏ
v i đ nh là các đi m l y trên hai đ ng th ng đã cho.ớ ỉ ể ấ ườ ẳ
Câu V.b. Theo ch ng trình THPT phân ban thí đi m ươ ể (2 đi m)ể
1. Gi i ph ng trình: ả ươ
2007 2006
2006 x 2007 x 1
− + − =
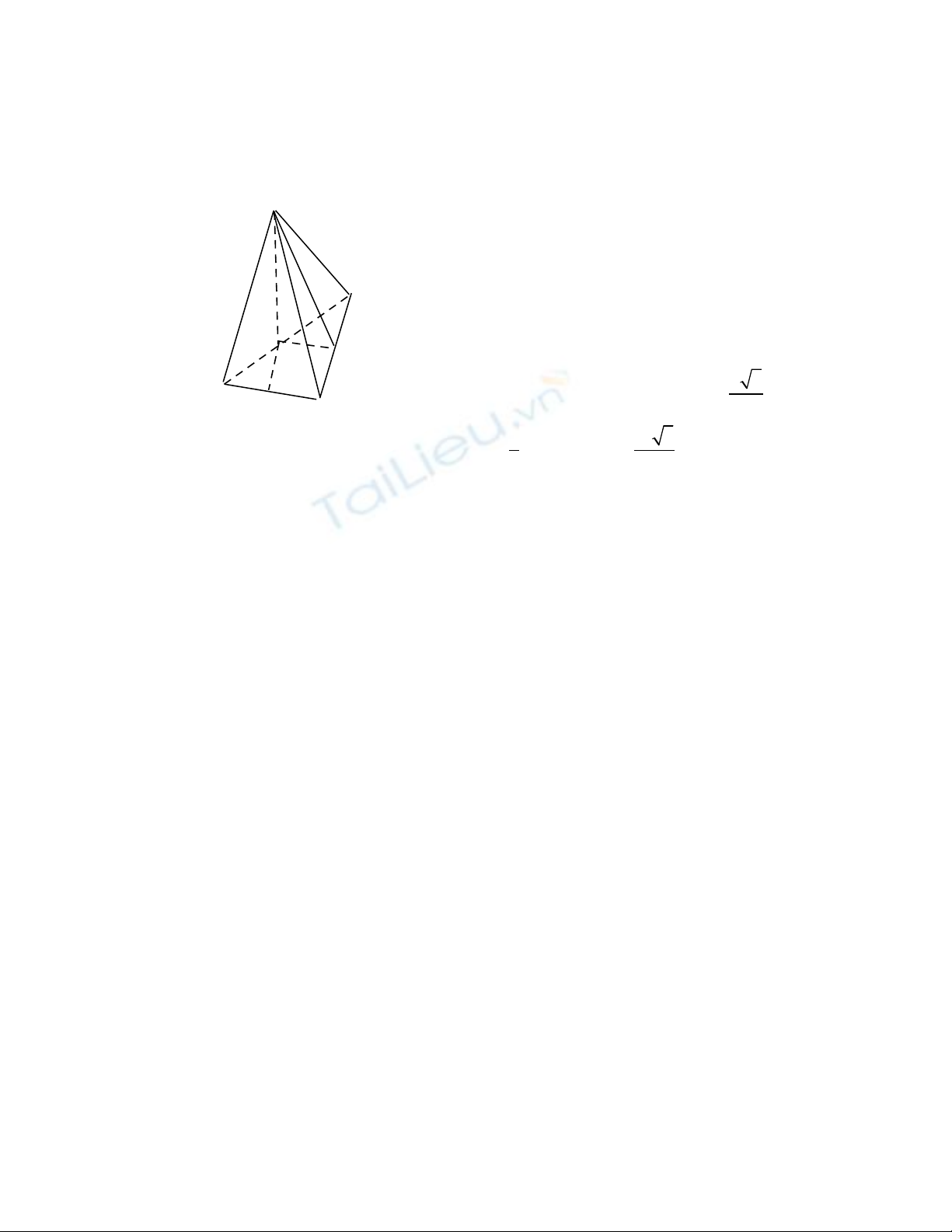
2. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân t i đ nh A (ạ ỉ
ﾵ
A
= 90o),
AB=AC=a. M t bên qua c nh huy n BC vuông góc v i m t đáy, hai m t bên cònặ ạ ề ớ ặ ặ
l i đ u h p v i m t đáy các góc 60ạ ề ợ ớ ặ o. Hãy tính th tích c a kh i chóp S.ABC.ể ủ ố
BÀI GI IẢ
Câu I. 1. m = 1 ⇒ y =
. MXĐ : D = R \ {1}. y' =
2
2
x 2x
(x 1)
−
−
; y’ = 0 ⇒ x = 0,
x = 2
TCĐ : x = 1; TCX : y = x
x−∞ 0 1 2 +∞
y' + 0 − − 0 +
y -1 +∞ +∞
−∞ −∞ 3
2. y =
2
x mx 2m 1
mx 1
− + −
−
; y’ =
2 2
2
mx 2x 2m 2m
(mx 1)
− − +
−
y =
2 3 2
2 2
x 1 m 2m 2m 1
m m m (mx 1)
− − +
+ + −
⇒ TCX : y =
2
2
x 1 m
m m
−
+
v i ớ
3 2
2m 2m 1 0
− +
và m ≠ 0
YCBT ⇔
2 2
2
3 2
2
mx 2x 2m 2m 0 có 2 nghiem phan biet
1 m
0 2m 2m 1 0 m 0
m
− − + =
−+− =ٹ� �
⇔ m = 1
Câu II. 1.
2 2
2 3 sin x
sin x sin x
3 3 2
π π −
� � � �
+ + + =
� � � �
� � � �
⇔
2 2
3 sin x
sin x sin x
3 3 2
π π −
� � � �
+ + − =
� � � �
� � � �
⇔
2 2
1 cos 2x 1 cos 2x 3 sin x
3 3
2 2 2
π π
� � � �
− + − −
� � � � −
� � � �
+ =
⇔
2 2
1 sin x cos 2x cos 2x 0
3 3
π π
� � � �
− + + + − =
� � � �
� � � �
⇔
1
1 sin x 2 cos 2x 0
2
� �
− + − =
� �
� �
⇔ 1 – cos2x – sinx = 0 ⇔ 2sin2x – sinx = 0
⇔
sin x 0
1
sin x 2
=
=
⇔
x k
x k2
6
5
x k2
6
= π
π
= + π
π
= + π
(k ∈ Z)
2. (I)
3 3
x y m(x y) (1)
x y 2 (2)
+ = +
− =
(2) ⇔ y = x − 2 thay vào (1) ta có :
(2x - 2)[x2 - 2x + 4 - m] = 0 ⇔
2
x 1
x 2x 4 m 0(*)
=
− + − =
Nh n xét : N u pt (*) có 2 nghi m xậ ế ệ 1, x2 phân bi t thì : xệ1 < 1 < x2 và x1 + x2 = 2
YCBT ⇔ pt (*) có 2 nghi m phân bi t ệ ệ ⇔ ∆' = 1 - 4 + m > 0 ⇔ m > 3.
Câu III. 1. a =
b 2
⇔ sinA = sin
B 2
Nên : cos2A = 1 - sin2A = 1 - 2sin2B = cos2B (đpcm)
Vì : cos2B = cos2A và 0 ≤ cos2A ≤ 1 nên : B l n nh t ớ ấ ⇔ cos2B nh nh t ỏ ấ ⇔
cos2B = 0
⇔ 2B = 90o ⇔ B = 450. Lúc đó : A= 90o, C = 45o.
2. I =
3
2
1
ln x dx
(x 1)+
. Đ t u = lnx ặ⇒ du =
dx
x
;dv = (x + 1)-2dx ⇒ v =
1
x 1
−+
I =
( )
33 3
11 1
x 1 x
ln x 1 1 1
dx ln 3 dx
x 1 x(x 1) 4 x x 1
+ − � �
− + = − + −
� �
+ + +
� �
� �
=
3
1
1 x
ln 3 ln
4 x 1
� �
− + � �
+
� �
=
1 3
ln 3 ln
4 2
− +
Câu IV. 1. Ta có :
AB ( 4;1;0)
= −
uuur
;
BC (2;1; 4)
= −
uuur
⇒
AB, BC ( 4; 16; 6) 0
� �
= − − −
� �
uuur uuur r
⇒ A, B, C không th ng hàng ẳ⇒ A, B, C là 3 đ nh c a tam giácỉ ủ
⇒ AH = d(A, BC) =
AB, BC 2 33
BC 3
� �
� �=
uuur uuur
2. M (m + 2; 1; 2n + 3) ⇒
AM (m 4;3; 2n)
= −
uuuur
cùng ph ng ươ
AC 2(1; 1; 2)
= − −
uuur
⇒
m 4 3 2n
1 1 2
−= =
−
⇒ m = 1 và n = -3
Câu V.a. 1. Gi s d qua M c t (H) t i A, B : v i M là trung đi m ABả ử ắ ạ ớ ể
A, B ∈ (H) : ⇒
2 2
A A
2 2
B B
3x 2y 6 (1)
3x 2y 6 (2)
− =
− =
M là trung đi m AB nên : xểA + xB = 4 (3) và yA + yB = 2 (4)
(1) − (2) ta có : 3(x2A - x2B) - 2(y2A - y2B) = 0 (5)
Thay (3) và (4) vào (5) ta có : 3(xA -xB)-(yA-yB) = 0 ⇔ 3(2xA-4)-(2yA- 2) = 0 ⇔ 3xA
- yA = 5
T ng t : 3xươ ự B - yB = 5. V y ph ng trình d : 3x - y - 5 = 0 ậ ươ
2. S tam giác có đ nh trên dố ỉ 1 và đáy trên d2 :
2
16
9.C
S tam giác có đ nh trên dố ỉ 2 và đáy trên d1 :
2
9
16.C
Số tam giác th a YCBT làỏ
2
16
9.C
+
2
9
16.C
.
Câu V.b.
1. Nh n xét : ậ
1 x 2006 1
1 x 2007 1
− −
− −
⇔ 2006 ≤ x ≤ 2007
Ta có : 2006 - x2007 + 2007 - x2006 ≤ 2006 - x+ 2007 - x = x - 2006 + 2007 - x
= 1
V y ph ng trình ậ ươ ⇔ 2006 - x2007 = 2006 - x và 2007 - x2006 = 2007 - x
⇔
2006 x 0
2006 x 1
2007 x 0
2007 x 1
− =�
− =
��
− =
− =
⇔
x 2006
x 2005
x 2007
x 2007
x 2006
=�
=
=
=
=
⇔ x = 2006 hay x = 2007
2. K SH vuông góc v i BC. Suy ra SH ẻ ớ ⊥ mp
(ABC)
K SI vuông góc v i AB và SJ ẻ ớ ⊥ AC
⇒góc SIH=góc SJH = 60o ⇒ tam giác SHI = tam
giác SHJ
⇒ HI = HJ ⇒ AIHJ là hình vuông
⇒ I là trung đi m AB ể⇒ IH = a/2
Trong tam giác vuông SHI ta có SH =
a 3
2
V(SABC) =
3
1 a 3
SH.dt(ABC)
3 12
=
(đvtt)
Ng i gi i đ : 0977467739 H t.ườ ả ề ế
I
HJ
S
B
C
A